Image Generation from Image Captioning -- Invertible Approach

Our work aims to build a model that performs dual tasks of image captioning and image generation while being trained on only one task. The central idea is to train an invertible model that learns a one-to-one mapping between the image and text embeddings. Once the invertible model is efficiently trained on one task, the image captioning, the same model can generate new images for a given text through the inversion process, with no additional training. This paper proposes a simple invertible neural network architecture for this problem and presents our current findings.

Activations Through Extensions: A Framework To Boost Performance Of Neural Networks

Activation functions are non-linearities in neural networks that allow them to learn complex mapping between inputs and outputs. Typical choices for activation functions are ReLU, Tanh, Sigmoid etc., where the choice generally depends on the application domain. In this work, we propose a framework/strategy that unifies several works on activation functions and theoretically explains the performance benefits of these works. We also propose novel techniques that originate from the framework and allow us to obtain ``extensions'' (i.e. special generalizations of a given neural network) of neural networks through operations on activation functions. We theoretically and empirically show that ``extensions'' of neural networks have performance benefits compared to vanilla neural networks with insignificant space and time complexity costs on standard test functions. We also show the benefits of neural network ``extensions'' in the time-series domain on real-world datasets.

An Application of Newsboy Problem in Supply Chain Optimisation of Online Fashion E-Commerce

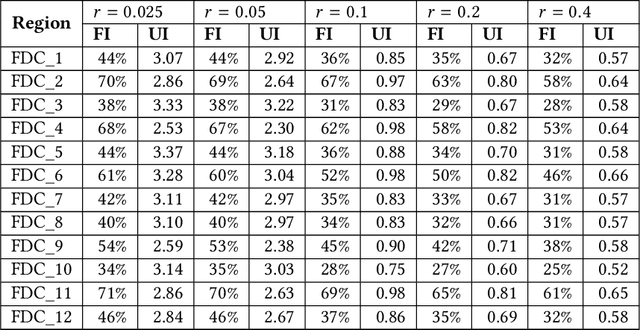
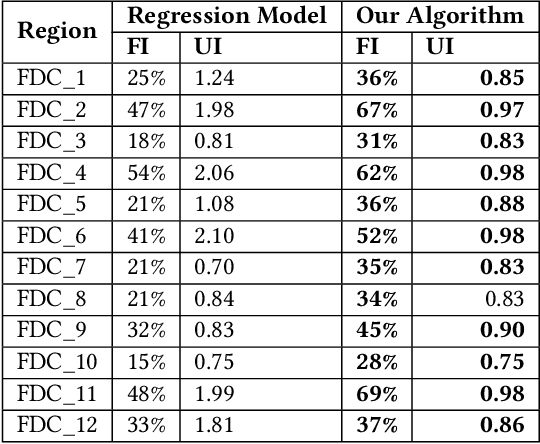
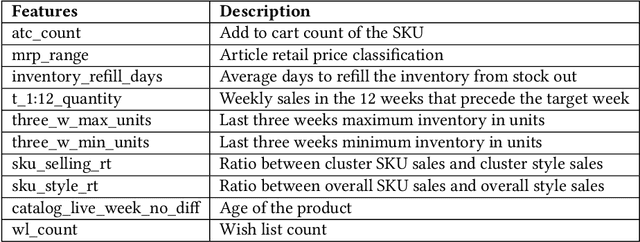
We describe a supply chain optimization model deployed in an online fashion e-commerce company in India called Myntra. Our model is simple, elegant and easy to put into service. The model utilizes historic data and predicts the quantity of Stock Keeping Units (SKUs) to hold so that the metrics "Fulfilment Index" and "Utilization Index" are optimized. We present the mathematics central to our model as well as compare the performance of our model with baseline regression based solutions.

A Convergent Off-Policy Temporal Difference Algorithm

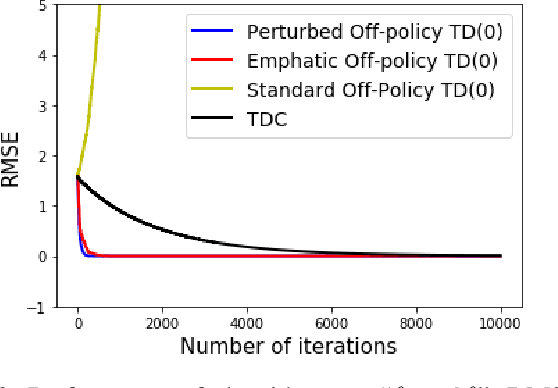
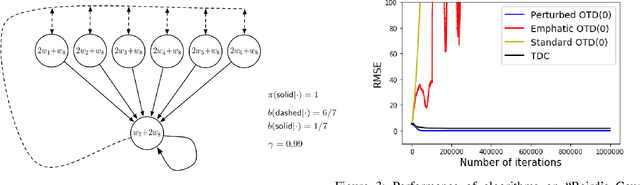
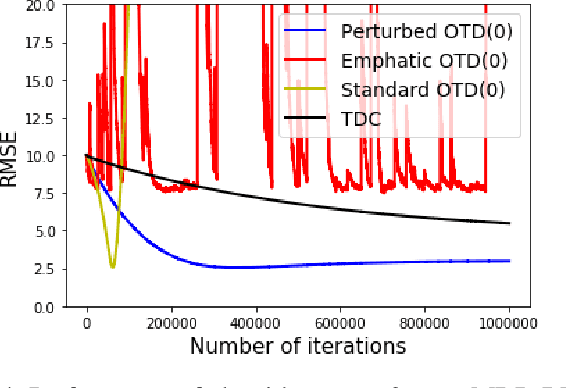
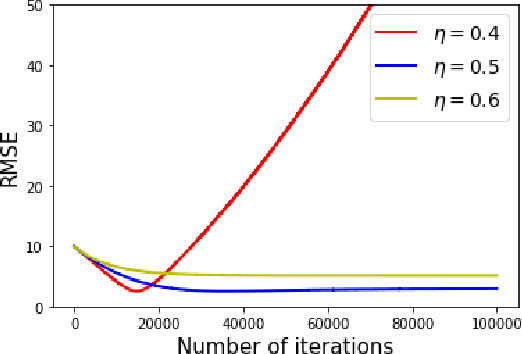
Learning the value function of a given policy (target policy) from the data samples obtained from a different policy (behavior policy) is an important problem in Reinforcement Learning (RL). This problem is studied under the setting of off-policy prediction. Temporal Difference (TD) learning algorithms are a popular class of algorithms for solving the prediction problem. TD algorithms with linear function approximation are shown to be convergent when the samples are generated from the target policy (known as on-policy prediction). However, it has been well established in the literature that off-policy TD algorithms under linear function approximation diverge. In this work, we propose a convergent on-line off-policy TD algorithm under linear function approximation. The main idea is to penalize the updates of the algorithm in a way as to ensure convergence of the iterates. We provide a convergence analysis of our algorithm. Through numerical evaluations, we further demonstrate the effectiveness of our algorithm.

Generalized Speedy Q-learning

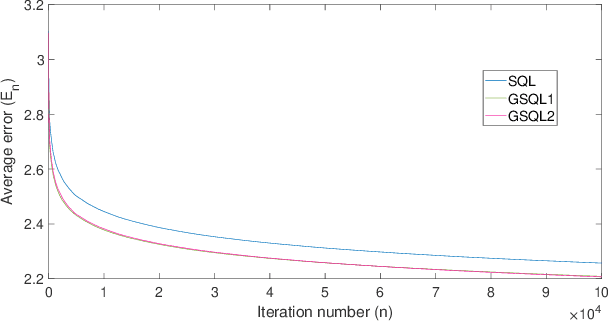
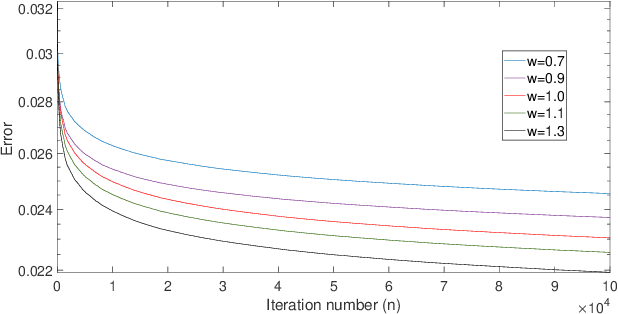
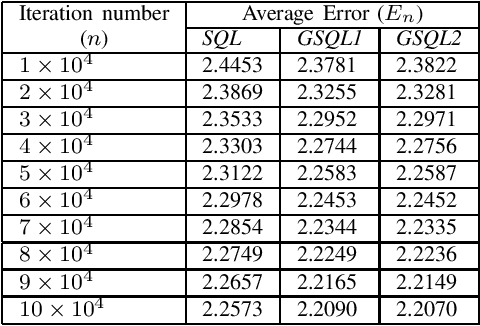
In this paper, we derive a generalization of the Speedy Q-learning (SQL) algorithm that was proposed in the Reinforcement Learning (RL) literature to handle slow convergence of Watkins' Q-learning. In most RL algorithms such as Q-learning, the Bellman equation and the Bellman operator play an important role. It is possible to generalize the Bellman operator using the technique of successive relaxation. We use the generalized Bellman operator to derive a simple and efficient family of algorithms called Generalized Speedy Q-learning (GSQL-w) and analyze its finite time performance. We show that GSQL-w has an improved finite time performance bound compared to SQL for the case when the relaxation parameter w is greater than 1. This improvement is a consequence of the contraction factor of the generalized Bellman operator being less than that of the standard Bellman operator. Numerical experiments are provided to demonstrate the empirical performance of the GSQL-w algorithm.

Solution of Two-Player Zero-Sum Game by Successive Relaxation

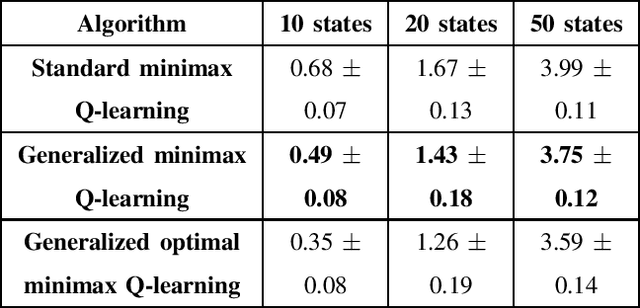
We consider the problem of two-player zero-sum game. In this setting, there are two agents working against each other. Both the agents observe the same state and the objective of the agents is to compute a strategy profile that maximizes their rewards. However, the reward of the second agent is negative of reward obtained by the first agent. Therefore, the objective of the second agent is to minimize the total reward obtained by the first agent. This problem is formulated as a min-max Markov game in the literature. The solution of this game, which is the max-min reward (of first player), starting from a given state is called the equilibrium value of the state. In this work, we compute the solution of the two-player zero-sum game utilizing the technique of successive relaxation. Successive relaxation has been successfully applied in the literature to compute a faster value iteration algorithm in the context of Markov Decision Processes. We extend the concept of successive relaxation to the two-player zero-sum games. We prove that, under a special structure, this technique computes the optimal solution faster than the techniques in the literature. We then derive a generalized minimax Q-learning algorithm that computes the optimal policy when the model information is not known. Finally, we prove the convergence of the proposed generalized minimax Q-learning algorithm.

Second Order Value Iteration in Reinforcement Learning

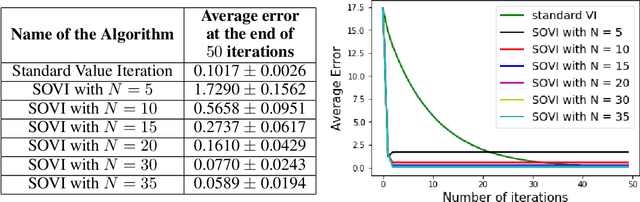
Value iteration is a fixed point iteration technique utilized to obtain the optimal value function and policy in a discounted reward Markov Decision Process (MDP). Here, a contraction operator is constructed and applied repeatedly to arrive at the optimal solution. Value iteration is a first order method and therefore it may take a large number of iterations to converge to the optimal solution. In this work, we propose a novel second order value iteration procedure based on the Newton-Raphson method. We first construct a modified contraction operator and then apply Newton-Raphson method to arrive at our algorithm. We prove the global convergence of our algorithm to the optimal solution and show the second order convergence. Through experiments, we demonstrate the effectiveness of our proposed approach.

Successive Over Relaxation Q-Learning

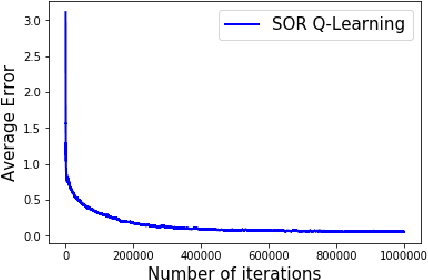
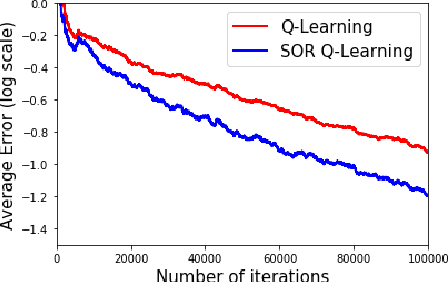
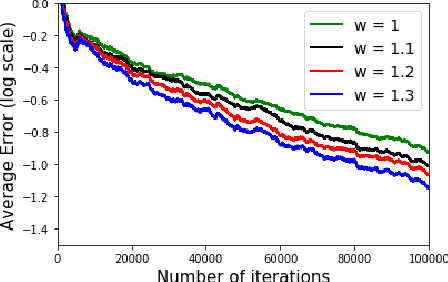
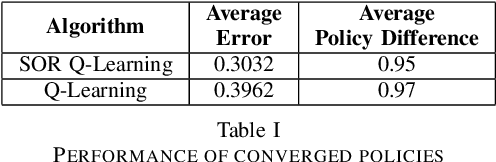
In a discounted reward Markov Decision Process (MDP) the objective is to find the optimal value function, i.e., the value function corresponding to an optimal policy. This problem reduces to solving a functional equation known as the Bellman equation and a fixed point iteration scheme known as the value iteration is utilized to obtain the solution. In [1], a successive over-relaxation based value iteration scheme is proposed to speed up the computation of the optimal value function. They propose a modified Bellman equation and prove faster convergence to the optimal value function. However, in many practical applications, the model information is not known and we resort to Reinforcement Learning (RL) algorithms to obtain optimal policy and value function. One such popular algorithm is Q-Learning. In this paper, we propose Successive Over Relaxation (SOR) Q-Learning. We first derive a fixed point iteration for optimal Q-values based on [1] and utilize stochastic approximation to derive a learning algorithm to compute the optimal value function and an optimal policy. We then prove the convergence of the SOR Q-Learning to optimal Q-values. Finally, through numerical experiments, we show that SOR Q-Learning is faster compared to the standard Q-Learning algorithm.

An Online Sample Based Method for Mode Estimation using ODE Analysis of Stochastic Approximation Algorithms

One of the popular measures of central tendency that provides better representation and interesting insights of the data compared to the other measures like mean and median is the metric mode. If the analytical form of the density function is known, mode is an argument of the maximum value of the density function and one can apply the optimization techniques to find mode. In many of the practical applications, the analytical form of the density is not known and only the samples from the distribution are available. Most of the techniques proposed in the literature for estimating the mode from the samples assume that all the samples are available beforehand. Moreover, some of the techniques employ computationally expensive operations like sorting. In this work we provide a computationally effective, on-line iterative algorithm that estimates the mode of a unimodal smooth density given only the samples generated from the density. Asymptotic convergence of the proposed algorithm using an ordinary differential equation (ODE) based analysis is provided. We also prove the stability of estimates by utilizing the concept of regularization. Experimental results further demonstrate the effectiveness of the proposed algorithm.