Successive Over Relaxation Q-Learning
Paper and Code
Mar 15, 2019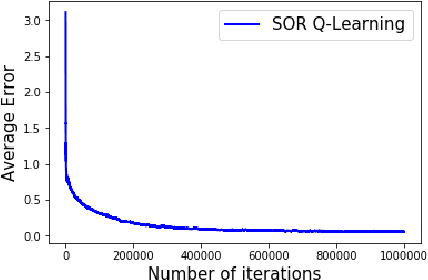
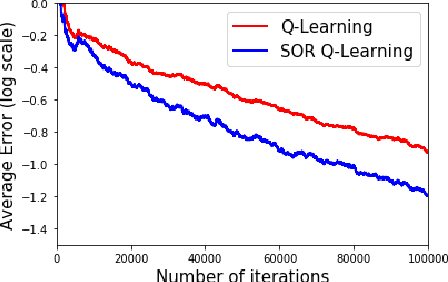
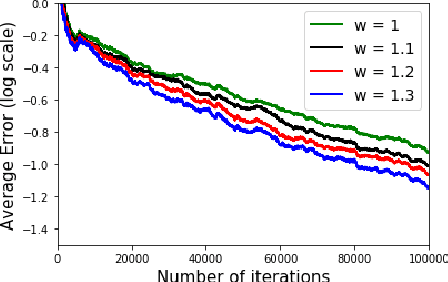
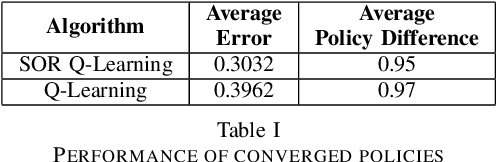
In a discounted reward Markov Decision Process (MDP) the objective is to find the optimal value function, i.e., the value function corresponding to an optimal policy. This problem reduces to solving a functional equation known as the Bellman equation and a fixed point iteration scheme known as the value iteration is utilized to obtain the solution. In [1], a successive over-relaxation based value iteration scheme is proposed to speed up the computation of the optimal value function. They propose a modified Bellman equation and prove faster convergence to the optimal value function. However, in many practical applications, the model information is not known and we resort to Reinforcement Learning (RL) algorithms to obtain optimal policy and value function. One such popular algorithm is Q-Learning. In this paper, we propose Successive Over Relaxation (SOR) Q-Learning. We first derive a fixed point iteration for optimal Q-values based on [1] and utilize stochastic approximation to derive a learning algorithm to compute the optimal value function and an optimal policy. We then prove the convergence of the SOR Q-Learning to optimal Q-values. Finally, through numerical experiments, we show that SOR Q-Learning is faster compared to the standard Q-Learning algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge