Full-Gradient Successor Feature Representations

Successor Features (SF) combined with Generalized Policy Improvement (GPI) provide a robust framework for transfer learning in Reinforcement Learning (RL) by decoupling environment dynamics from reward functions. However, standard SF learning methods typically rely on semi-gradient Temporal Difference (TD) updates. When combined with non-linear function approximation, semi-gradient methods lack robust convergence guarantees and can lead to instability, particularly in the multi-task setting where accurate feature estimation is critical for effective GPI. Inspired by Full Gradient DQN, we propose Full-Gradient Successor Feature Representations Q-Learning (FG-SFRQL), an algorithm that optimizes the successor features by minimizing the full Mean Squared Bellman Error. Unlike standard approaches, our method computes gradients with respect to parameters in both the online and target networks. We provide a theoretical proof of almost-sure convergence for FG-SFRQL and demonstrate empirically that minimizing the full residual leads to superior sample efficiency and transfer performance compared to semi-gradient baselines in both discrete and continuous domains.

Generalisation in Multitask Fitted Q-Iteration and Offline Q-learning

We study offline multitask reinforcement learning in settings where multiple tasks share a low-rank representation of their action-value functions. In this regime, a learner is provided with fixed datasets collected from several related tasks, without access to further online interaction, and seeks to exploit shared structure to improve statistical efficiency and generalization. We analyze a multitask variant of fitted Q-iteration that jointly learns a shared representation and task-specific value functions via Bellman error minimization on offline data. Under standard realizability and coverage assumptions commonly used in offline reinforcement learning, we establish finite-sample generalization guarantees for the learned value functions. Our analysis explicitly characterizes how pooling data across tasks improves estimation accuracy, yielding a $1/\sqrt{nT}$ dependence on the total number of samples across tasks, while retaining the usual dependence on the horizon and concentrability coefficients arising from distribution shift. In addition, we consider a downstream offline setting in which a new task shares the same underlying representation as the upstream tasks. We study how reusing the representation learned during the multitask phase affects value estimation for this new task, and show that it can reduce the effective complexity of downstream learning relative to learning from scratch. Together, our results clarify the role of shared representations in multitask offline Q-learning and provide theoretical insight into when and how multitask structure can improve generalization in model-free, value-based reinforcement learning.

Image Generation from Image Captioning -- Invertible Approach

Our work aims to build a model that performs dual tasks of image captioning and image generation while being trained on only one task. The central idea is to train an invertible model that learns a one-to-one mapping between the image and text embeddings. Once the invertible model is efficiently trained on one task, the image captioning, the same model can generate new images for a given text through the inversion process, with no additional training. This paper proposes a simple invertible neural network architecture for this problem and presents our current findings.

Neural Network Compatible Off-Policy Natural Actor-Critic Algorithm

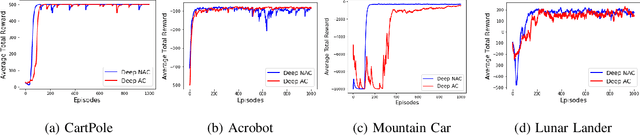
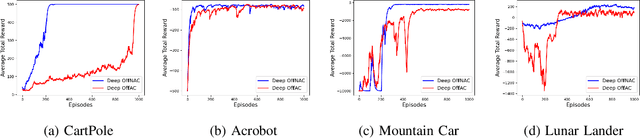
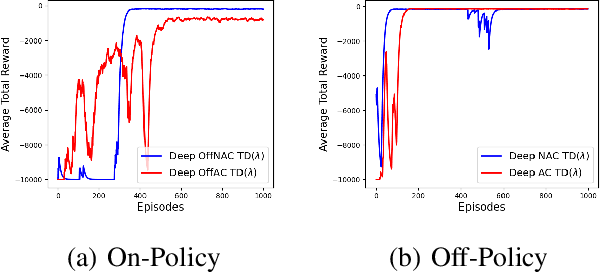
Learning optimal behavior from existing data is one of the most important problems in Reinforcement Learning (RL). This is known as "off-policy control" in RL where an agent's objective is to compute an optimal policy based on the data obtained from the given policy (known as the behavior policy). As the optimal policy can be very different from the behavior policy, learning optimal behavior is very hard in the "off-policy" setting compared to the "on-policy" setting where new data from the policy updates will be utilized in learning. This work proposes an off-policy natural actor-critic algorithm that utilizes state-action distribution correction for handling the off-policy behavior and the natural policy gradient for sample efficiency. The existing natural gradient-based actor-critic algorithms with convergence guarantees require fixed features for approximating both policy and value functions. This often leads to sub-optimal learning in many RL applications. On the other hand, our proposed algorithm utilizes compatible features that enable one to use arbitrary neural networks to approximate the policy and the value function and guarantee convergence to a locally optimal policy. We illustrate the benefit of the proposed off-policy natural gradient algorithm by comparing it with the vanilla gradient actor-critic algorithm on benchmark RL tasks.

Attention Actor-Critic algorithm for Multi-Agent Constrained Co-operative Reinforcement Learning

In this work, we consider the problem of computing optimal actions for Reinforcement Learning (RL) agents in a co-operative setting, where the objective is to optimize a common goal. However, in many real-life applications, in addition to optimizing the goal, the agents are required to satisfy certain constraints specified on their actions. Under this setting, the objective of the agents is to not only learn the actions that optimize the common objective but also meet the specified constraints. In recent times, the Actor-Critic algorithm with an attention mechanism has been successfully applied to obtain optimal actions for RL agents in multi-agent environments. In this work, we extend this algorithm to the constrained multi-agent RL setting. The idea here is that optimizing the common goal and satisfying the constraints may require different modes of attention. By incorporating different attention modes, the agents can select useful information required for optimizing the objective and satisfying the constraints separately, thereby yielding better actions. Through experiments on benchmark multi-agent environments, we show the effectiveness of our proposed algorithm.

A Convergent Off-Policy Temporal Difference Algorithm

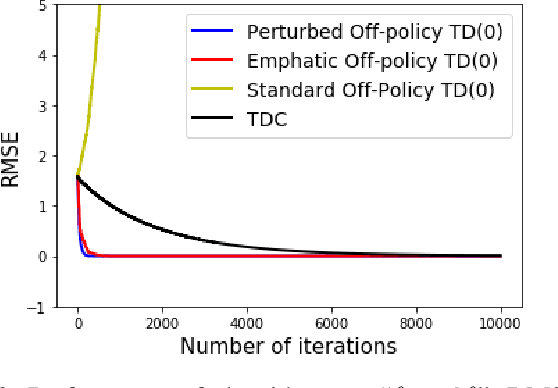
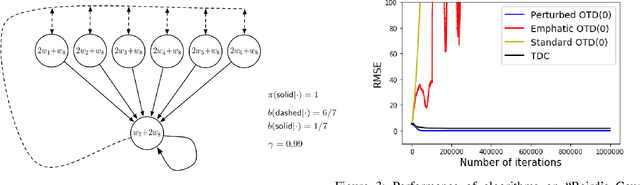
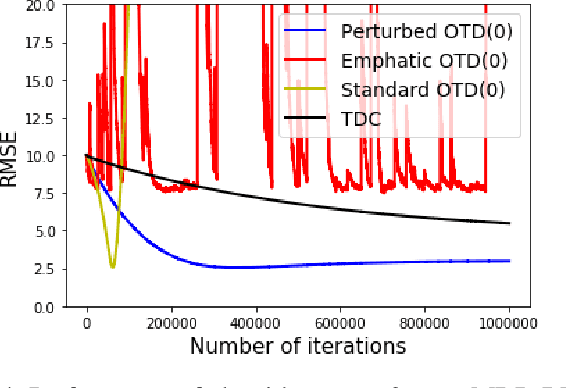
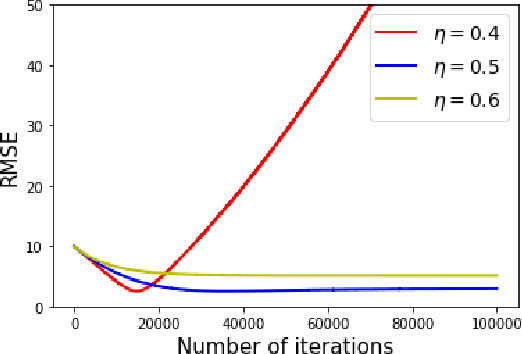
Learning the value function of a given policy (target policy) from the data samples obtained from a different policy (behavior policy) is an important problem in Reinforcement Learning (RL). This problem is studied under the setting of off-policy prediction. Temporal Difference (TD) learning algorithms are a popular class of algorithms for solving the prediction problem. TD algorithms with linear function approximation are shown to be convergent when the samples are generated from the target policy (known as on-policy prediction). However, it has been well established in the literature that off-policy TD algorithms under linear function approximation diverge. In this work, we propose a convergent on-line off-policy TD algorithm under linear function approximation. The main idea is to penalize the updates of the algorithm in a way as to ensure convergence of the iterates. We provide a convergence analysis of our algorithm. Through numerical evaluations, we further demonstrate the effectiveness of our algorithm.

Solution of Two-Player Zero-Sum Game by Successive Relaxation

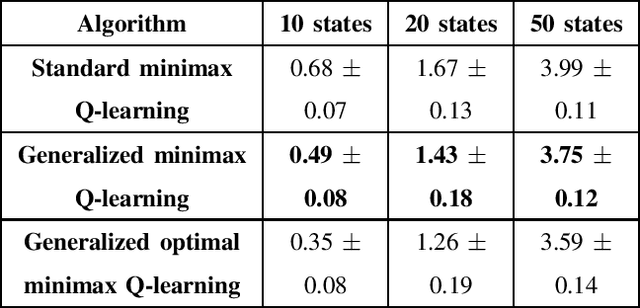
We consider the problem of two-player zero-sum game. In this setting, there are two agents working against each other. Both the agents observe the same state and the objective of the agents is to compute a strategy profile that maximizes their rewards. However, the reward of the second agent is negative of reward obtained by the first agent. Therefore, the objective of the second agent is to minimize the total reward obtained by the first agent. This problem is formulated as a min-max Markov game in the literature. The solution of this game, which is the max-min reward (of first player), starting from a given state is called the equilibrium value of the state. In this work, we compute the solution of the two-player zero-sum game utilizing the technique of successive relaxation. Successive relaxation has been successfully applied in the literature to compute a faster value iteration algorithm in the context of Markov Decision Processes. We extend the concept of successive relaxation to the two-player zero-sum games. We prove that, under a special structure, this technique computes the optimal solution faster than the techniques in the literature. We then derive a generalized minimax Q-learning algorithm that computes the optimal policy when the model information is not known. Finally, we prove the convergence of the proposed generalized minimax Q-learning algorithm.

Second Order Value Iteration in Reinforcement Learning

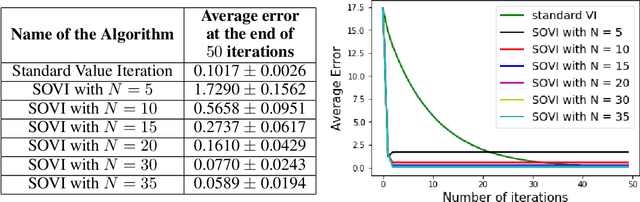
Value iteration is a fixed point iteration technique utilized to obtain the optimal value function and policy in a discounted reward Markov Decision Process (MDP). Here, a contraction operator is constructed and applied repeatedly to arrive at the optimal solution. Value iteration is a first order method and therefore it may take a large number of iterations to converge to the optimal solution. In this work, we propose a novel second order value iteration procedure based on the Newton-Raphson method. We first construct a modified contraction operator and then apply Newton-Raphson method to arrive at our algorithm. We prove the global convergence of our algorithm to the optimal solution and show the second order convergence. Through experiments, we demonstrate the effectiveness of our proposed approach.

Successive Over Relaxation Q-Learning

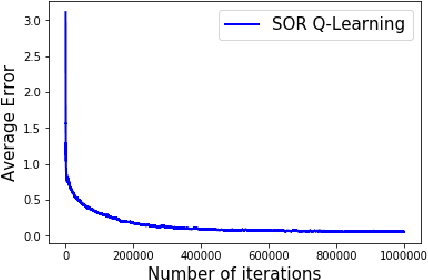
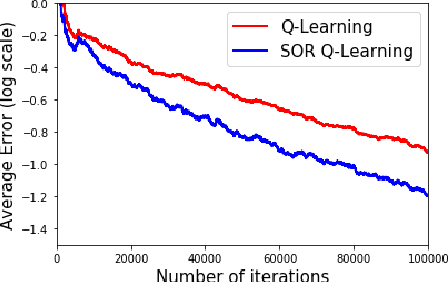
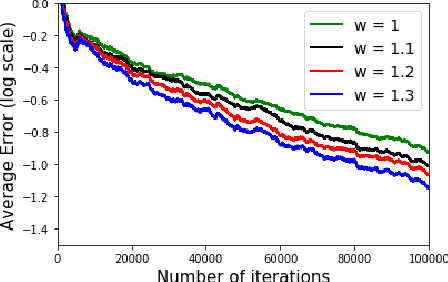
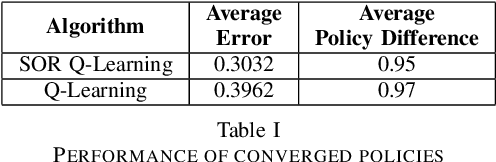
In a discounted reward Markov Decision Process (MDP) the objective is to find the optimal value function, i.e., the value function corresponding to an optimal policy. This problem reduces to solving a functional equation known as the Bellman equation and a fixed point iteration scheme known as the value iteration is utilized to obtain the solution. In [1], a successive over-relaxation based value iteration scheme is proposed to speed up the computation of the optimal value function. They propose a modified Bellman equation and prove faster convergence to the optimal value function. However, in many practical applications, the model information is not known and we resort to Reinforcement Learning (RL) algorithms to obtain optimal policy and value function. One such popular algorithm is Q-Learning. In this paper, we propose Successive Over Relaxation (SOR) Q-Learning. We first derive a fixed point iteration for optimal Q-values based on [1] and utilize stochastic approximation to derive a learning algorithm to compute the optimal value function and an optimal policy. We then prove the convergence of the SOR Q-Learning to optimal Q-values. Finally, through numerical experiments, we show that SOR Q-Learning is faster compared to the standard Q-Learning algorithm.

An Online Sample Based Method for Mode Estimation using ODE Analysis of Stochastic Approximation Algorithms

One of the popular measures of central tendency that provides better representation and interesting insights of the data compared to the other measures like mean and median is the metric mode. If the analytical form of the density function is known, mode is an argument of the maximum value of the density function and one can apply the optimization techniques to find mode. In many of the practical applications, the analytical form of the density is not known and only the samples from the distribution are available. Most of the techniques proposed in the literature for estimating the mode from the samples assume that all the samples are available beforehand. Moreover, some of the techniques employ computationally expensive operations like sorting. In this work we provide a computationally effective, on-line iterative algorithm that estimates the mode of a unimodal smooth density given only the samples generated from the density. Asymptotic convergence of the proposed algorithm using an ordinary differential equation (ODE) based analysis is provided. We also prove the stability of estimates by utilizing the concept of regularization. Experimental results further demonstrate the effectiveness of the proposed algorithm.