A Convergent Off-Policy Temporal Difference Algorithm
Paper and Code
Nov 13, 2019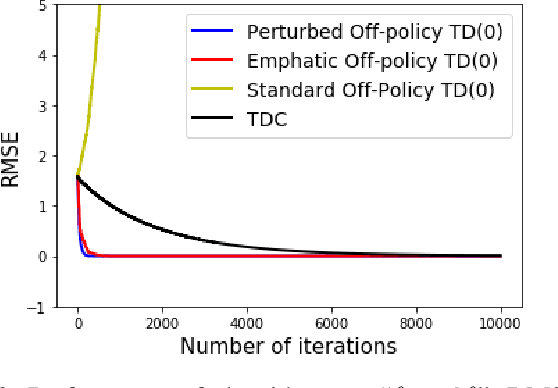
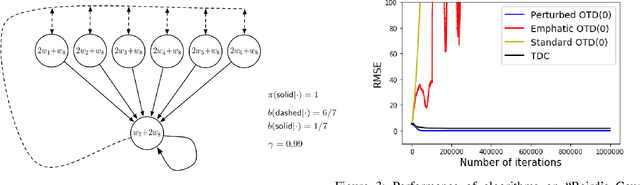
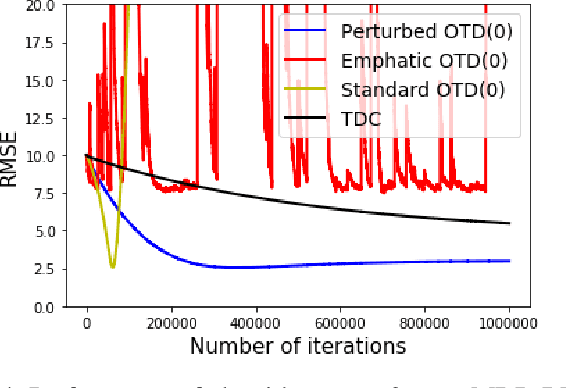
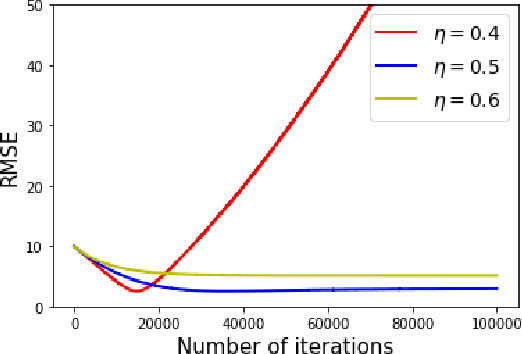
Learning the value function of a given policy (target policy) from the data samples obtained from a different policy (behavior policy) is an important problem in Reinforcement Learning (RL). This problem is studied under the setting of off-policy prediction. Temporal Difference (TD) learning algorithms are a popular class of algorithms for solving the prediction problem. TD algorithms with linear function approximation are shown to be convergent when the samples are generated from the target policy (known as on-policy prediction). However, it has been well established in the literature that off-policy TD algorithms under linear function approximation diverge. In this work, we propose a convergent on-line off-policy TD algorithm under linear function approximation. The main idea is to penalize the updates of the algorithm in a way as to ensure convergence of the iterates. We provide a convergence analysis of our algorithm. Through numerical evaluations, we further demonstrate the effectiveness of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge