Practical First-Order Bayesian Optimization Algorithms

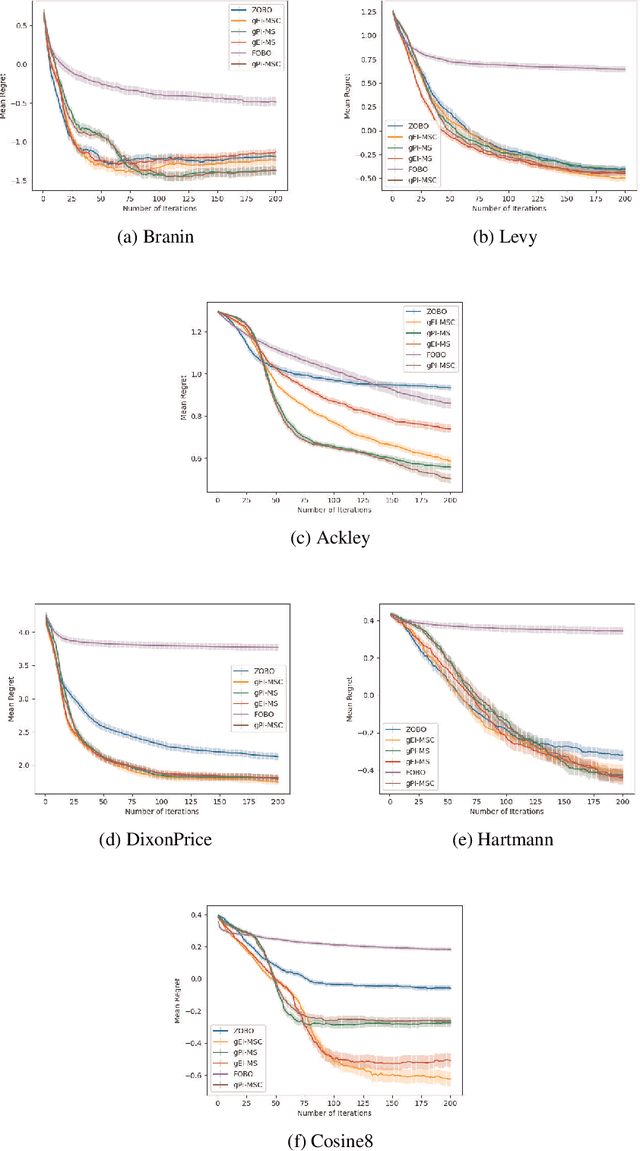
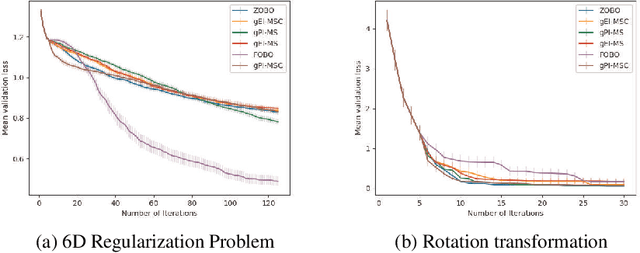
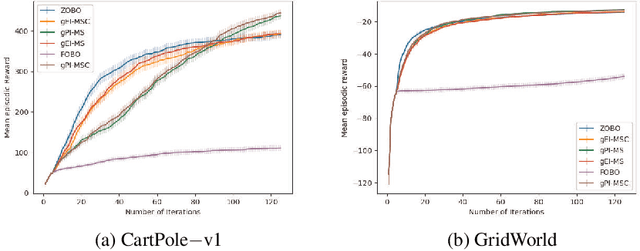
First Order Bayesian Optimization (FOBO) is a sample efficient sequential approach to find the global maxima of an expensive-to-evaluate black-box objective function by suitably querying for the function and its gradient evaluations. Such methods assume Gaussian process (GP) models for both, the function and its gradient, and use them to construct an acquisition function that identifies the next query point. In this paper, we propose a class of practical FOBO algorithms that efficiently utilizes the information from the gradient GP to identify potential query points with zero gradients. We construct a multi-level acquisition function where in the first step, we optimize a lower level acquisition function with multiple restarts to identify potential query points with zero gradient value. We then use the upper level acquisition function to rank these query points based on their function values to potentially identify the global maxima. As a final step, the potential point of maxima is chosen as the actual query point. We validate the performance of our proposed algorithms on several test functions and show that our algorithms outperform state-of-the-art FOBO algorithms. We also illustrate the application of our algorithms in finding optimal set of hyper-parameters in machine learning and in learning the optimal policy in reinforcement learning tasks.

Bayesian Optimization for Function Compositions with Applications to Dynamic Pricing

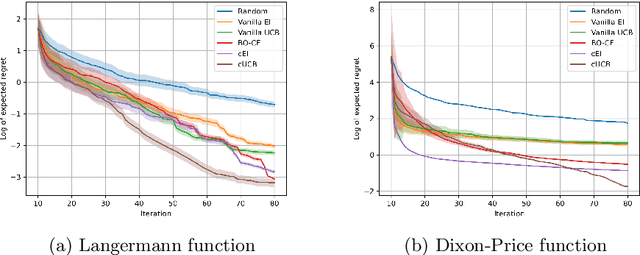
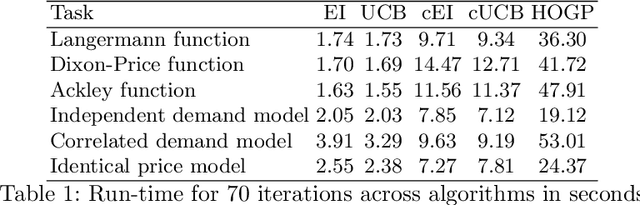
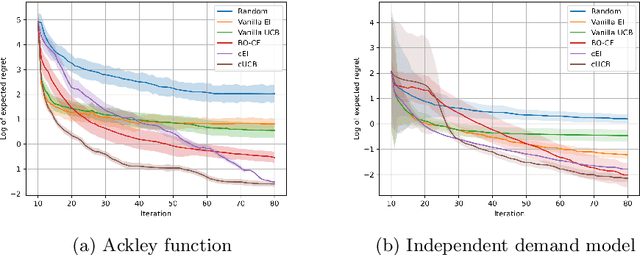
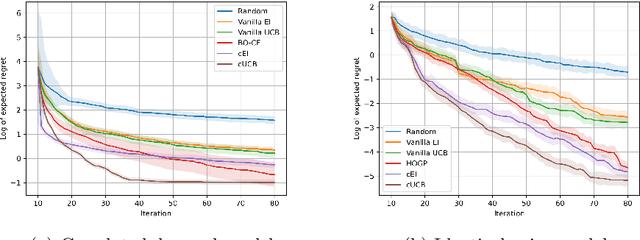
Bayesian Optimization (BO) is used to find the global optima of black box functions. In this work, we propose a practical BO method of function compositions where the form of the composition is known but the constituent functions are expensive to evaluate. By assuming an independent Gaussian process (GP) model for each of the constituent black-box function, we propose EI and UCB based BO algorithms and demonstrate their ability to outperform vanilla BO and the current state-of-art algorithms. We demonstrate a novel application of the proposed methods to dynamic pricing in revenue management when the underlying demand function is expensive to evaluate.

Neural Network Compatible Off-Policy Natural Actor-Critic Algorithm

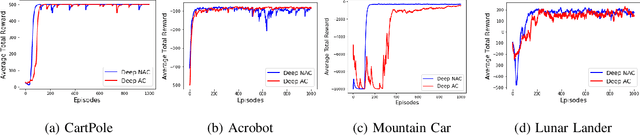
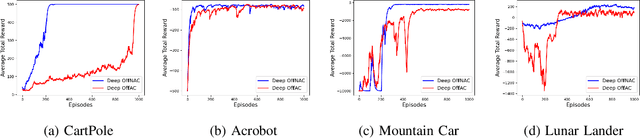
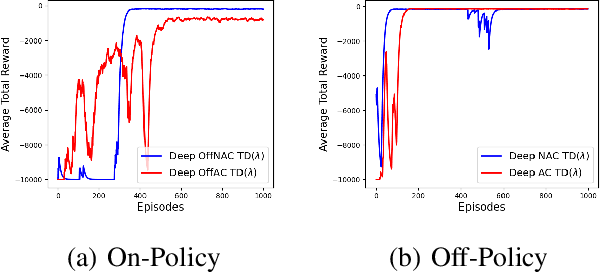
Learning optimal behavior from existing data is one of the most important problems in Reinforcement Learning (RL). This is known as "off-policy control" in RL where an agent's objective is to compute an optimal policy based on the data obtained from the given policy (known as the behavior policy). As the optimal policy can be very different from the behavior policy, learning optimal behavior is very hard in the "off-policy" setting compared to the "on-policy" setting where new data from the policy updates will be utilized in learning. This work proposes an off-policy natural actor-critic algorithm that utilizes state-action distribution correction for handling the off-policy behavior and the natural policy gradient for sample efficiency. The existing natural gradient-based actor-critic algorithms with convergence guarantees require fixed features for approximating both policy and value functions. This often leads to sub-optimal learning in many RL applications. On the other hand, our proposed algorithm utilizes compatible features that enable one to use arbitrary neural networks to approximate the policy and the value function and guarantee convergence to a locally optimal policy. We illustrate the benefit of the proposed off-policy natural gradient algorithm by comparing it with the vanilla gradient actor-critic algorithm on benchmark RL tasks.

An Online Sample Based Method for Mode Estimation using ODE Analysis of Stochastic Approximation Algorithms

One of the popular measures of central tendency that provides better representation and interesting insights of the data compared to the other measures like mean and median is the metric mode. If the analytical form of the density function is known, mode is an argument of the maximum value of the density function and one can apply the optimization techniques to find mode. In many of the practical applications, the analytical form of the density is not known and only the samples from the distribution are available. Most of the techniques proposed in the literature for estimating the mode from the samples assume that all the samples are available beforehand. Moreover, some of the techniques employ computationally expensive operations like sorting. In this work we provide a computationally effective, on-line iterative algorithm that estimates the mode of a unimodal smooth density given only the samples generated from the density. Asymptotic convergence of the proposed algorithm using an ordinary differential equation (ODE) based analysis is provided. We also prove the stability of estimates by utilizing the concept of regularization. Experimental results further demonstrate the effectiveness of the proposed algorithm.

Novel Sensor Scheduling Scheme for Intruder Tracking in Energy Efficient Sensor Networks

We consider the problem of tracking an intruder using a network of wireless sensors. For tracking the intruder at each instant, the optimal number and the right configuration of sensors has to be powered. As powering the sensors consumes energy, there is a trade off between accurately tracking the position of the intruder at each instant and the energy consumption of sensors. This problem has been formulated in the framework of Partially Observable Markov Decision Process (POMDP). Even for the state-of-the-art algorithm in the literature, the curse of dimensionality renders the problem intractable. In this paper, we formulate the Intrusion Detection (ID) problem with a suitable state-action space in the framework of POMDP and develop a Reinforcement Learning (RL) algorithm utilizing the Upper Confidence Tree Search (UCT) method to solve the ID problem. Through simulations, we show that our algorithm performs and scales well with the increasing state and action spaces.