Tabular and Deep Reinforcement Learning for Gittins Index

In the realm of multi-arm bandit problems, the Gittins index policy is known to be optimal in maximizing the expected total discounted reward obtained from pulling the Markovian arms. In most realistic scenarios however, the Markovian state transition probabilities are unknown and therefore the Gittins indices cannot be computed. One can then resort to reinforcement learning (RL) algorithms that explore the state space to learn these indices while exploiting to maximize the reward collected. In this work, we propose tabular (QGI) and Deep RL (DGN) algorithms for learning the Gittins index that are based on the retirement formulation for the multi-arm bandit problem. When compared with existing RL algorithms that learn the Gittins index, our algorithms have a lower run time, require less storage space (small Q-table size in QGI and smaller replay buffer in DGN), and illustrate better empirical convergence to the Gittins index. This makes our algorithm well suited for problems with large state spaces and is a viable alternative to existing methods. As a key application, we demonstrate the use of our algorithms in minimizing the mean flowtime in a job scheduling problem when jobs are available in batches and have an unknown service time distribution. \

Mixture Density Networks for Classification with an Application to Product Bundling

While mixture density networks (MDNs) have been extensively used for regression tasks, they have not been used much for classification tasks. One reason for this is that the usability of MDNs for classification is not clear and straightforward. In this paper, we propose two MDN-based models for classification tasks. Both models fit mixtures of Gaussians to the the data and use the fitted distributions to classify a given sample by evaluating the learnt cumulative distribution function for the given input features. While the proposed MDN-based models perform slightly better than, or on par with, five baseline classification models on three publicly available datasets, the real utility of our models comes out through a real-world product bundling application. Specifically, we use our MDN-based models to learn the willingness-to-pay (WTP) distributions for two products from synthetic sales data of the individual products. The Gaussian mixture representation of the learnt WTP distributions is then exploited to obtain the WTP distribution of the bundle consisting of both the products. The proposed MDN-based models are able to approximate the true WTP distributions of both products and the bundle well.

Practical First-Order Bayesian Optimization Algorithms

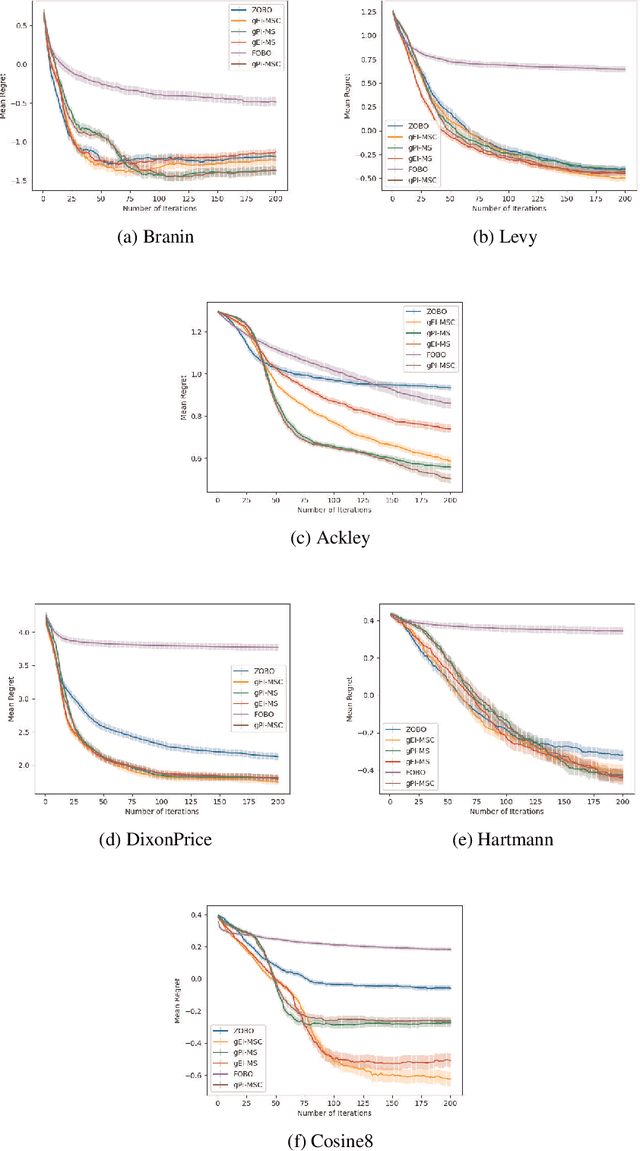
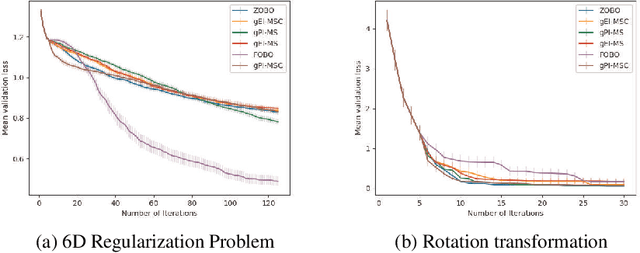
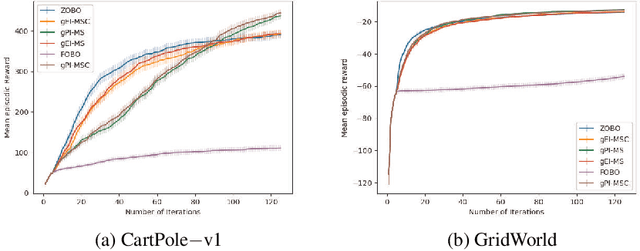
First Order Bayesian Optimization (FOBO) is a sample efficient sequential approach to find the global maxima of an expensive-to-evaluate black-box objective function by suitably querying for the function and its gradient evaluations. Such methods assume Gaussian process (GP) models for both, the function and its gradient, and use them to construct an acquisition function that identifies the next query point. In this paper, we propose a class of practical FOBO algorithms that efficiently utilizes the information from the gradient GP to identify potential query points with zero gradients. We construct a multi-level acquisition function where in the first step, we optimize a lower level acquisition function with multiple restarts to identify potential query points with zero gradient value. We then use the upper level acquisition function to rank these query points based on their function values to potentially identify the global maxima. As a final step, the potential point of maxima is chosen as the actual query point. We validate the performance of our proposed algorithms on several test functions and show that our algorithms outperform state-of-the-art FOBO algorithms. We also illustrate the application of our algorithms in finding optimal set of hyper-parameters in machine learning and in learning the optimal policy in reinforcement learning tasks.

Bayesian Optimization for Function Compositions with Applications to Dynamic Pricing

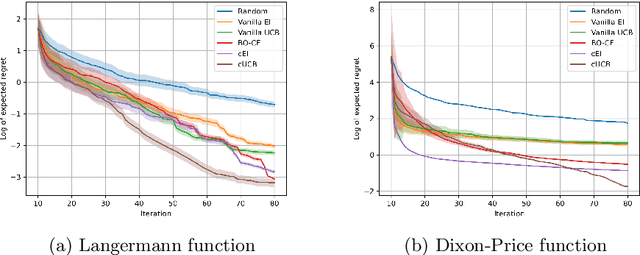
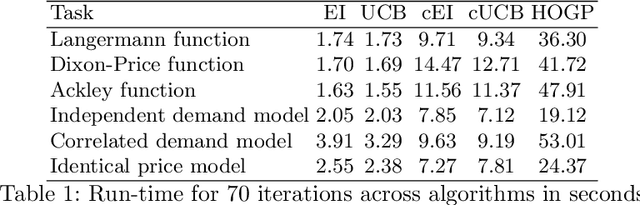
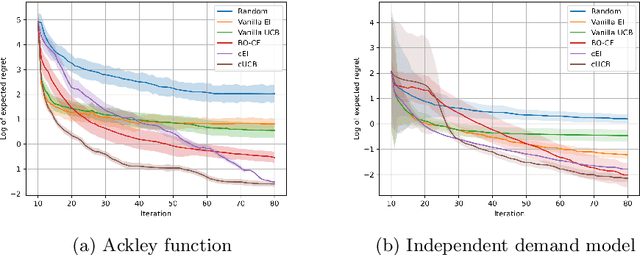
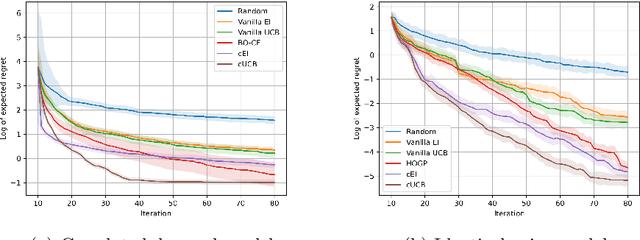
Bayesian Optimization (BO) is used to find the global optima of black box functions. In this work, we propose a practical BO method of function compositions where the form of the composition is known but the constituent functions are expensive to evaluate. By assuming an independent Gaussian process (GP) model for each of the constituent black-box function, we propose EI and UCB based BO algorithms and demonstrate their ability to outperform vanilla BO and the current state-of-art algorithms. We demonstrate a novel application of the proposed methods to dynamic pricing in revenue management when the underlying demand function is expensive to evaluate.

Reinforcement Learning algorithms for regret minimization in structured Markov Decision Processes

A recent goal in the Reinforcement Learning (RL) framework is to choose a sequence of actions or a policy to maximize the reward collected or minimize the regret incurred in a finite time horizon. For several RL problems in operation research and optimal control, the optimal policy of the underlying Markov Decision Process (MDP) is characterized by a known structure. The current state of the art algorithms do not utilize this known structure of the optimal policy while minimizing regret. In this work, we develop new RL algorithms that exploit the structure of the optimal policy to minimize regret. Numerical experiments on MDPs with structured optimal policies show that our algorithms have better performance, are easy to implement, have a smaller run-time and require less number of random number generations.