Mixture Density Networks for Classification with an Application to Product Bundling

While mixture density networks (MDNs) have been extensively used for regression tasks, they have not been used much for classification tasks. One reason for this is that the usability of MDNs for classification is not clear and straightforward. In this paper, we propose two MDN-based models for classification tasks. Both models fit mixtures of Gaussians to the the data and use the fitted distributions to classify a given sample by evaluating the learnt cumulative distribution function for the given input features. While the proposed MDN-based models perform slightly better than, or on par with, five baseline classification models on three publicly available datasets, the real utility of our models comes out through a real-world product bundling application. Specifically, we use our MDN-based models to learn the willingness-to-pay (WTP) distributions for two products from synthetic sales data of the individual products. The Gaussian mixture representation of the learnt WTP distributions is then exploited to obtain the WTP distribution of the bundle consisting of both the products. The proposed MDN-based models are able to approximate the true WTP distributions of both products and the bundle well.

Optimization of utility-based shortfall risk: A non-asymptotic viewpoint

We consider the problems of estimation and optimization of utility-based shortfall risk (UBSR), which is a popular risk measure in finance. In the context of UBSR estimation, we derive a non-asymptotic bound on the mean-squared error of the classical sample average approximation (SAA) of UBSR. Next, in the context of UBSR optimization, we derive an expression for the UBSR gradient under a smooth parameterization. This expression is a ratio of expectations, both of which involve the UBSR. We use SAA for the numerator as well as denominator in the UBSR gradient expression to arrive at a biased gradient estimator. We derive non-asymptotic bounds on the estimation error, which show that our gradient estimator is asymptotically unbiased. We incorporate the aforementioned gradient estimator into a stochastic gradient (SG) algorithm for UBSR optimization. Finally, we derive non-asymptotic bounds that quantify the rate of convergence of our SG algorithm for UBSR optimization.

Estimation of Spectral Risk Measures

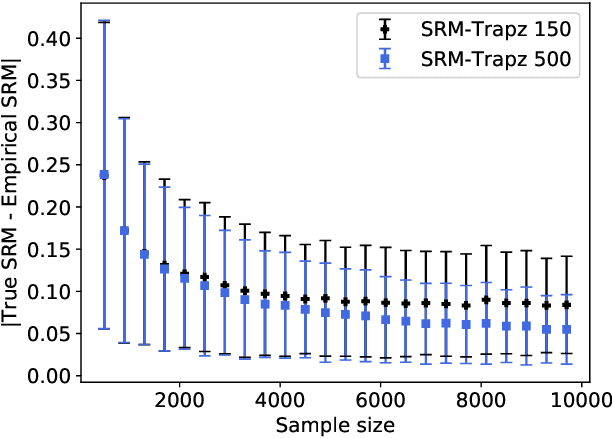
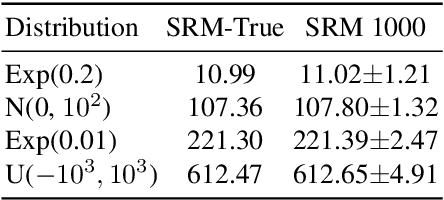
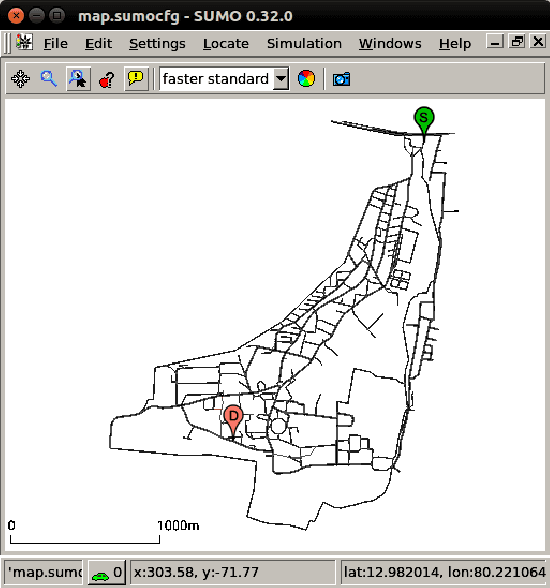
We consider the problem of estimating a spectral risk measure (SRM) from i.i.d. samples, and propose a novel method that is based on numerical integration. We show that our SRM estimate concentrates exponentially, when the underlying distribution has bounded support. Further, we also consider the case when the underlying distribution is either Gaussian or exponential, and derive a concentration bound for our estimation scheme. We validate the theoretical findings on a synthetic setup, and in a vehicular traffic routing application.

Improved Concentration Bounds for Conditional Value-at-Risk and Cumulative Prospect Theory using Wasserstein distance

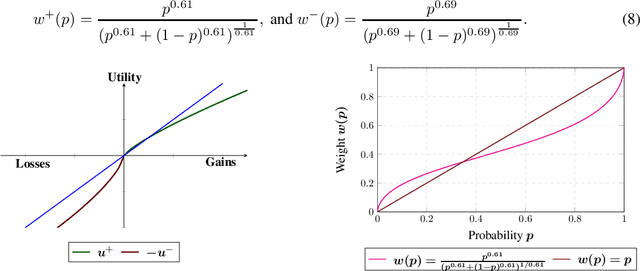
Known finite-sample concentration bounds for the Wasserstein distance between the empirical and true distribution of a random variable are used to derive a two-sided concentration bound for the error between the true conditional value-at-risk (CVaR) of a (possibly unbounded) random variable and a standard estimate of its CVaR computed from an i.i.d. sample. The bound applies under fairly general assumptions on the random variable, and improves upon previous bounds which were either one sided, or applied only to bounded random variables. Specializations of the bound to sub-Gaussian and sub-exponential random variables are also derived. A similar procedure is followed to derive concentration bounds for the error between the true and estimated Cumulative Prospect Theory (CPT) value of a random variable, in cases where the random variable is bounded or sub-Gaussian. These bounds are shown to match a known bound in the bounded case, and improve upon the known bound in the sub-Gaussian case. The usefulness of the bounds is illustrated through an algorithm, and corresponding regret bound for a stochastic bandit problem, where the underlying risk measure to be optimized is CVaR.

Concentration bounds for empirical conditional value-at-risk: The unbounded case

In several real-world applications involving decision making under uncertainty, the traditional expected value objective may not be suitable, as it may be necessary to control losses in the case of a rare but extreme event. Conditional Value-at-Risk (CVaR) is a popular risk measure for modeling the aforementioned objective. We consider the problem of estimating CVaR from i.i.d. samples of an unbounded random variable, which is either sub-Gaussian or sub-exponential. We derive a novel one-sided concentration bound for a natural sample-based CVaR estimator in this setting. Our bound relies on a concentration result for a quantile-based estimator for Value-at-Risk (VaR), which may be of independent interest.