Generalized Simultaneous Perturbation Stochastic Approximation with Reduced Estimator Bias

We present in this paper a family of generalized simultaneous perturbation stochastic approximation (G-SPSA) estimators that estimate the gradient of the objective using noisy function measurements, but where the number of function measurements and the form of the gradient estimator is guided by the desired estimator bias. In particular, estimators with more function measurements are seen to result in lower bias. We provide an analysis of convergence of the generalized SPSA algorithm, and point to possible future directions.

Approximate gradient ascent methods for distortion risk measures

We propose approximate gradient ascent algorithms for risk-sensitive reinforcement learning control problem in on-policy as well as off-policy settings. We consider episodic Markov decision processes, and model the risk using distortion risk measure (DRM) of the cumulative discounted reward. Our algorithms estimate the DRM using order statistics of the cumulative rewards, and calculate approximate gradients from the DRM estimates using a smoothed functional-based gradient estimation scheme. We derive non-asymptotic bounds that establish the convergence of our proposed algorithms to an approximate stationary point of the DRM objective.

Likelihood ratio-based policy gradient methods for distorted risk measures: A non-asymptotic analysis

We propose policy-gradient algorithms for solving the problem of control in a risk-sensitive reinforcement learning (RL) context. The objective of our algorithm is to maximize the distorted risk measure (DRM) of the cumulative reward in an episodic Markov decision process (MDP). We derive a variant of the policy gradient theorem that caters to the DRM objective. Using this theorem in conjunction with a likelihood ratio (LR) based gradient estimation scheme, we propose policy gradient algorithms for optimizing DRM in both on-policy and off-policy RL settings. We derive non-asymptotic bounds that establish the convergence of our algorithms to an approximate stationary point of the DRM objective.

Smoothed functional-based gradient algorithms for off-policy reinforcement learning

We consider the problem of control in an off-policy reinforcement learning (RL) context. We propose a policy gradient scheme that incorporates a smoothed functional-based gradient estimation scheme. We provide an asymptotic convergence guarantee for the proposed algorithm using the ordinary differential equation (ODE) approach. Further, we derive a non-asymptotic bound that quantifies the rate of convergence of the proposed algorithm.

Improved Concentration Bounds for Conditional Value-at-Risk and Cumulative Prospect Theory using Wasserstein distance

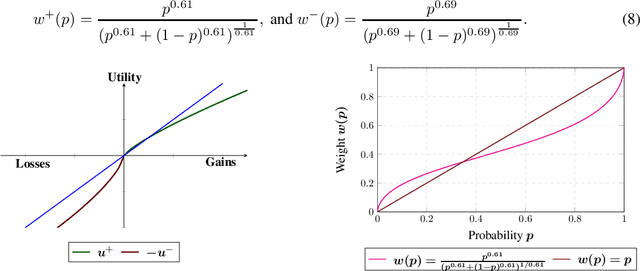
Known finite-sample concentration bounds for the Wasserstein distance between the empirical and true distribution of a random variable are used to derive a two-sided concentration bound for the error between the true conditional value-at-risk (CVaR) of a (possibly unbounded) random variable and a standard estimate of its CVaR computed from an i.i.d. sample. The bound applies under fairly general assumptions on the random variable, and improves upon previous bounds which were either one sided, or applied only to bounded random variables. Specializations of the bound to sub-Gaussian and sub-exponential random variables are also derived. A similar procedure is followed to derive concentration bounds for the error between the true and estimated Cumulative Prospect Theory (CPT) value of a random variable, in cases where the random variable is bounded or sub-Gaussian. These bounds are shown to match a known bound in the bounded case, and improve upon the known bound in the sub-Gaussian case. The usefulness of the bounds is illustrated through an algorithm, and corresponding regret bound for a stochastic bandit problem, where the underlying risk measure to be optimized is CVaR.

Correlated bandits or: How to minimize mean-squared error online

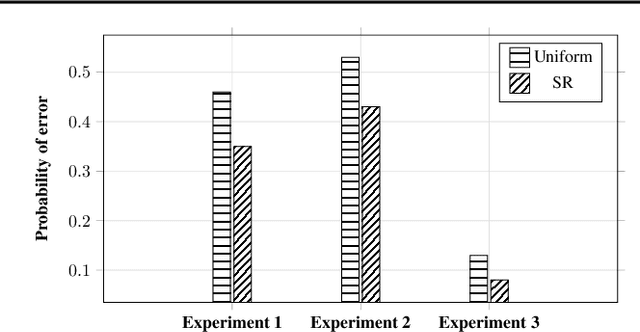
While the objective in traditional multi-armed bandit problems is to find the arm with the highest mean, in many settings, finding an arm that best captures information about other arms is of interest. This objective, however, requires learning the underlying correlation structure and not just the means. Sensors placement for industrial surveillance and cellular network monitoring are a few applications, where the underlying correlation structure plays an important role. Motivated by such applications, we formulate the correlated bandit problem, where the objective is to find the arm with the lowest mean-squared error (MSE) in estimating all the arms. To this end, we derive first an MSE estimator based on sample variances/covariances and show that our estimator exponentially concentrates around the true MSE. Under a best-arm identification framework, we propose a successive rejects type algorithm and provide bounds on the probability of error in identifying the best arm. Using minimax theory, we also derive fundamental performance limits for the correlated bandit problem.