Correlated bandits or: How to minimize mean-squared error online

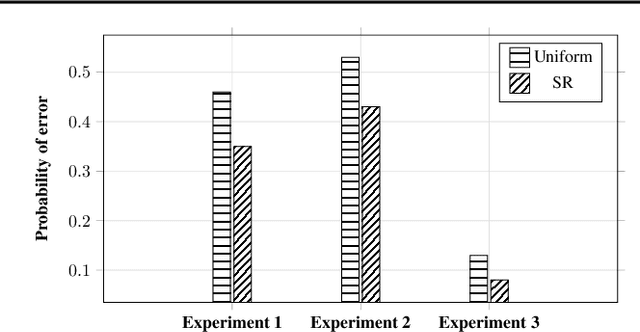
While the objective in traditional multi-armed bandit problems is to find the arm with the highest mean, in many settings, finding an arm that best captures information about other arms is of interest. This objective, however, requires learning the underlying correlation structure and not just the means. Sensors placement for industrial surveillance and cellular network monitoring are a few applications, where the underlying correlation structure plays an important role. Motivated by such applications, we formulate the correlated bandit problem, where the objective is to find the arm with the lowest mean-squared error (MSE) in estimating all the arms. To this end, we derive first an MSE estimator based on sample variances/covariances and show that our estimator exponentially concentrates around the true MSE. Under a best-arm identification framework, we propose a successive rejects type algorithm and provide bounds on the probability of error in identifying the best arm. Using minimax theory, we also derive fundamental performance limits for the correlated bandit problem.

Reconstructing Gaussian sources by spatial sampling

Consider a Gaussian memoryless multiple source with $m$ components with joint probability distribution known only to lie in a given class of distributions. A subset of $k \leq m$ components are sampled and compressed with the objective of reconstructing all the $m$ components within a specified level of distortion under a mean-squared error criterion. In Bayesian and nonBayesian settings, the notion of universal sampling rate distortion function for Gaussian sources is introduced to capture the optimal tradeoffs among sampling, compression rate and distortion level. Single-letter characterizations are provided for the universal sampling rate distortion function. Our achievability proofs highlight the following structural property: it is optimal to compress and reconstruct first the sampled components of the GMMS alone, and then form estimates for the unsampled components based on the former.

Universal Sampling Rate Distortion

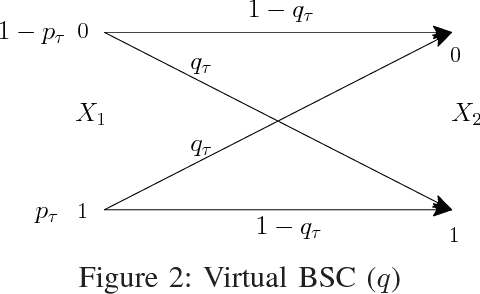
We examine the coordinated and universal rate-efficient sampling of a subset of correlated discrete memoryless sources followed by lossy compression of the sampled sources. The goal is to reconstruct a predesignated subset of sources within a specified level of distortion. The combined sampling mechanism and rate distortion code are universal in that they are devised to perform robustly without exact knowledge of the underlying joint probability distribution of the sources. In Bayesian as well as nonBayesian settings, single-letter characterizations are provided for the universal sampling rate distortion function for fixed-set sampling, independent random sampling and memoryless random sampling. It is illustrated how these sampling mechanisms are successively better. Our achievability proofs bring forth new schemes for joint source distribution-learning and lossy compression.

MKL-RT: Multiple Kernel Learning for Ratio-trace Problems via Convex Optimization

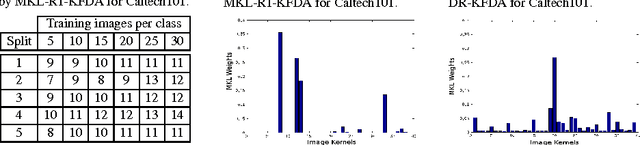
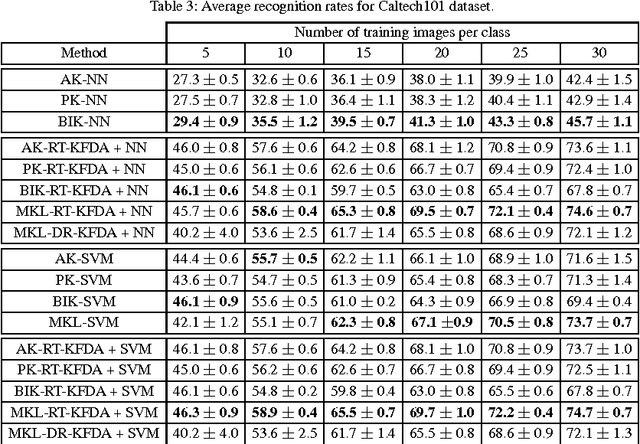
In the recent past, automatic selection or combination of kernels (or features) based on multiple kernel learning (MKL) approaches has been receiving significant attention from various research communities. Though MKL has been extensively studied in the context of support vector machines (SVM), it is relatively less explored for ratio-trace problems. In this paper, we show that MKL can be formulated as a convex optimization problem for a general class of ratio-trace problems that encompasses many popular algorithms used in various computer vision applications. We also provide an optimization procedure that is guaranteed to converge to the global optimum of the proposed optimization problem. We experimentally demonstrate that the proposed MKL approach, which we refer to as MKL-RT, can be successfully used to select features for discriminative dimensionality reduction and cross-modal retrieval. We also show that the proposed convex MKL-RT approach performs better than the recently proposed non-convex MKL-DR approach.