MKL-RT: Multiple Kernel Learning for Ratio-trace Problems via Convex Optimization
Paper and Code
Oct 17, 2014

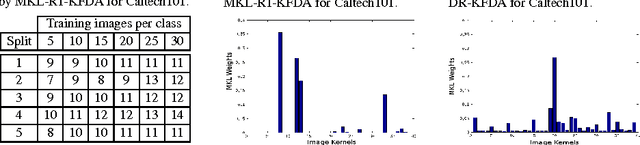
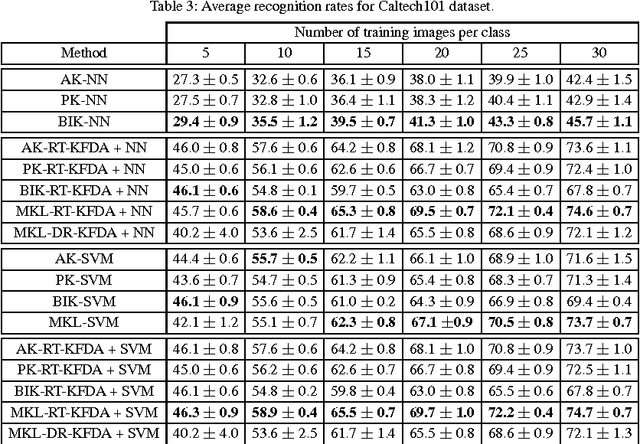
In the recent past, automatic selection or combination of kernels (or features) based on multiple kernel learning (MKL) approaches has been receiving significant attention from various research communities. Though MKL has been extensively studied in the context of support vector machines (SVM), it is relatively less explored for ratio-trace problems. In this paper, we show that MKL can be formulated as a convex optimization problem for a general class of ratio-trace problems that encompasses many popular algorithms used in various computer vision applications. We also provide an optimization procedure that is guaranteed to converge to the global optimum of the proposed optimization problem. We experimentally demonstrate that the proposed MKL approach, which we refer to as MKL-RT, can be successfully used to select features for discriminative dimensionality reduction and cross-modal retrieval. We also show that the proposed convex MKL-RT approach performs better than the recently proposed non-convex MKL-DR approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge