Risk-aware Multi-armed Bandits Using Conditional Value-at-Risk

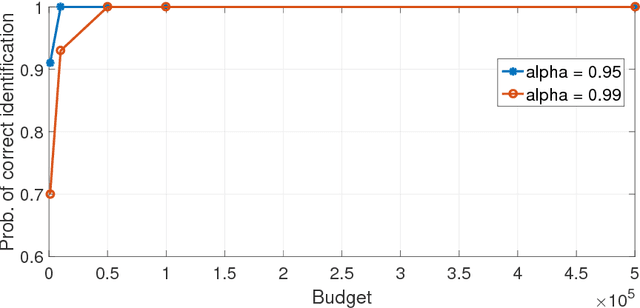
Traditional multi-armed bandit problems are geared towards finding the arm with the highest expected value -- an objective that is risk-neutral. In several practical applications, e.g., finance, a risk-sensitive objective is to control the worst-case losses and Conditional Value-at-Risk (CVaR) is a popular risk measure for modelling the aforementioned objective. We consider the CVaR optimization problem in a best-arm identification framework under a fixed budget. First, we derive a novel two-sided concentration bound for a well-known CVaR estimator using empirical distribution function, assuming that the underlying distribution is unbounded, but either sub-Gaussian or light-tailed. This bound may be of independent interest. Second, we adapt the well-known successive rejects algorithm to incorporate a CVaR-based criterion and derive an upper-bound on the probability of incorrect identification of our proposed algorithm.

Concentration bounds for empirical conditional value-at-risk: The unbounded case

In several real-world applications involving decision making under uncertainty, the traditional expected value objective may not be suitable, as it may be necessary to control losses in the case of a rare but extreme event. Conditional Value-at-Risk (CVaR) is a popular risk measure for modeling the aforementioned objective. We consider the problem of estimating CVaR from i.i.d. samples of an unbounded random variable, which is either sub-Gaussian or sub-exponential. We derive a novel one-sided concentration bound for a natural sample-based CVaR estimator in this setting. Our bound relies on a concentration result for a quantile-based estimator for Value-at-Risk (VaR), which may be of independent interest.

Collaborative Learning of Stochastic Bandits over a Social Network

We consider a collaborative online learning paradigm, wherein a group of agents connected through a social network are engaged in playing a stochastic multi-armed bandit game. Each time an agent takes an action, the corresponding reward is instantaneously observed by the agent, as well as its neighbours in the social network. We perform a regret analysis of various policies in this collaborative learning setting. A key finding of this paper is that natural extensions of widely-studied single agent learning policies to the network setting need not perform well in terms of regret. In particular, we identify a class of non-altruistic and individually consistent policies, and argue by deriving regret lower bounds that they are liable to suffer a large regret in the networked setting. We also show that the learning performance can be substantially improved if the agents exploit the structure of the network, and develop a simple learning algorithm based on dominating sets of the network. Specifically, we first consider a star network, which is a common motif in hierarchical social networks, and show analytically that the hub agent can be used as an information sink to expedite learning and improve the overall regret. We also derive networkwide regret bounds for the algorithm applied to general networks. We conduct numerical experiments on a variety of networks to corroborate our analytical results.