Non-Asymptotic Bounds for Zeroth-Order Stochastic Optimization

We consider the problem of optimizing an objective function with and without convexity in a simulation-optimization context, where only stochastic zeroth-order information is available. We consider two techniques for estimating gradient/Hessian, namely simultaneous perturbation (SP) and Gaussian smoothing (GS). We introduce an optimization oracle to capture a setting where the function measurements have an estimation error that can be controlled. Our oracle is appealing in several practical contexts where the objective has to be estimated from i.i.d. samples, and increasing the number of samples reduces the estimation error. In the stochastic non-convex optimization context, we analyze the zeroth-order variant of the randomized stochastic gradient (RSG) and quasi-Newton (RSQN) algorithms with a biased gradient/Hessian oracle, and with its variant involving an estimation error component. In particular, we provide non-asymptotic bounds on the performance of both algorithms, and our results provide a guideline for choosing the batch size for estimation, so that the overall error bound matches with the one obtained when there is no estimation error. Next, in the stochastic convex optimization setting, we provide non-asymptotic bounds that hold in expectation for the last iterate of a stochastic gradient descent (SGD) algorithm, and our bound for the GS variant of SGD matches the bound for SGD with unbiased gradient information. We perform simulation experiments on synthetic as well as real-world datasets, and the empirical results validate the theoretical findings.

Risk-aware Multi-armed Bandits Using Conditional Value-at-Risk

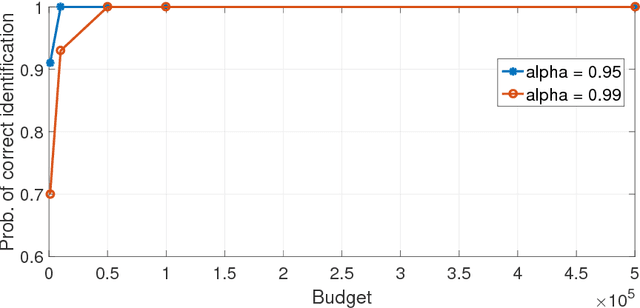
Traditional multi-armed bandit problems are geared towards finding the arm with the highest expected value -- an objective that is risk-neutral. In several practical applications, e.g., finance, a risk-sensitive objective is to control the worst-case losses and Conditional Value-at-Risk (CVaR) is a popular risk measure for modelling the aforementioned objective. We consider the CVaR optimization problem in a best-arm identification framework under a fixed budget. First, we derive a novel two-sided concentration bound for a well-known CVaR estimator using empirical distribution function, assuming that the underlying distribution is unbounded, but either sub-Gaussian or light-tailed. This bound may be of independent interest. Second, we adapt the well-known successive rejects algorithm to incorporate a CVaR-based criterion and derive an upper-bound on the probability of incorrect identification of our proposed algorithm.

Random directions stochastic approximation with deterministic perturbations

We introduce deterministic perturbation schemes for the recently proposed random directions stochastic approximation (RDSA) [17], and propose new first-order and second-order algorithms. In the latter case, these are the first second-order algorithms to incorporate deterministic perturbations. We show that the gradient and/or Hessian estimates in the resulting algorithms with deterministic perturbations are asymptotically unbiased, so that the algorithms are provably convergent. Furthermore, we derive convergence rates to establish the superiority of the first-order and second-order algorithms, for the special case of a convex and quadratic optimization problem, respectively. Numerical experiments are used to validate the theoretical results.