Risk-aware Multi-armed Bandits Using Conditional Value-at-Risk

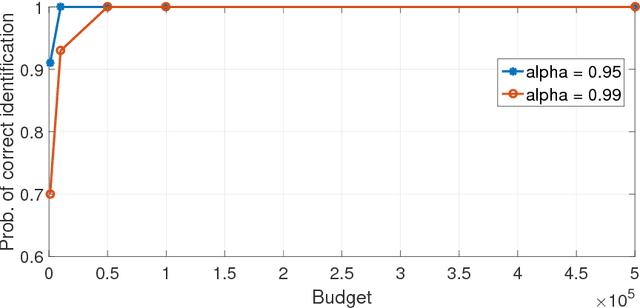
Traditional multi-armed bandit problems are geared towards finding the arm with the highest expected value -- an objective that is risk-neutral. In several practical applications, e.g., finance, a risk-sensitive objective is to control the worst-case losses and Conditional Value-at-Risk (CVaR) is a popular risk measure for modelling the aforementioned objective. We consider the CVaR optimization problem in a best-arm identification framework under a fixed budget. First, we derive a novel two-sided concentration bound for a well-known CVaR estimator using empirical distribution function, assuming that the underlying distribution is unbounded, but either sub-Gaussian or light-tailed. This bound may be of independent interest. Second, we adapt the well-known successive rejects algorithm to incorporate a CVaR-based criterion and derive an upper-bound on the probability of incorrect identification of our proposed algorithm.