Second Order Value Iteration in Reinforcement Learning

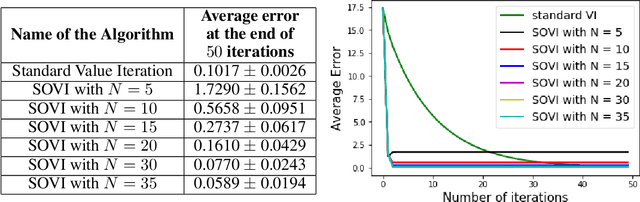
Value iteration is a fixed point iteration technique utilized to obtain the optimal value function and policy in a discounted reward Markov Decision Process (MDP). Here, a contraction operator is constructed and applied repeatedly to arrive at the optimal solution. Value iteration is a first order method and therefore it may take a large number of iterations to converge to the optimal solution. In this work, we propose a novel second order value iteration procedure based on the Newton-Raphson method. We first construct a modified contraction operator and then apply Newton-Raphson method to arrive at our algorithm. We prove the global convergence of our algorithm to the optimal solution and show the second order convergence. Through experiments, we demonstrate the effectiveness of our proposed approach.