CaloChallenge 2022: A Community Challenge for Fast Calorimeter Simulation

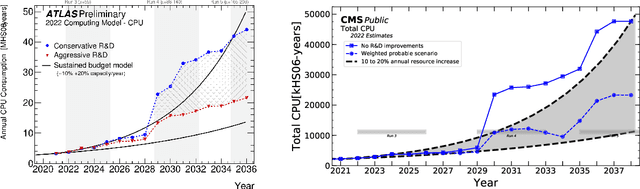
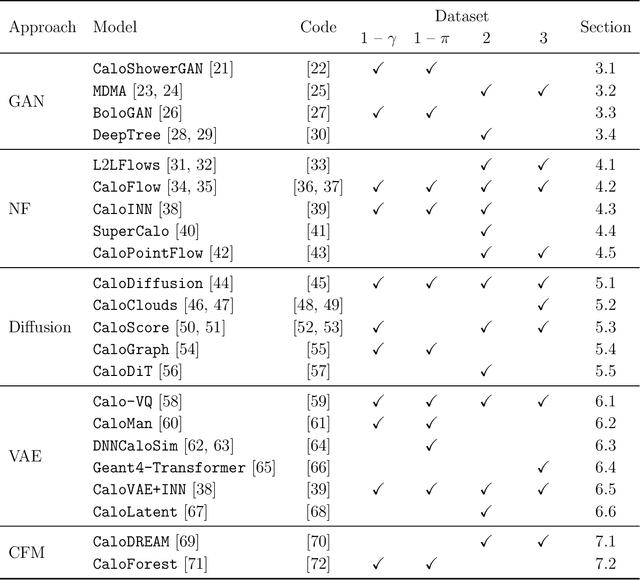
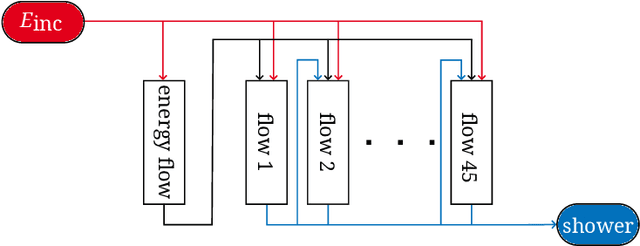
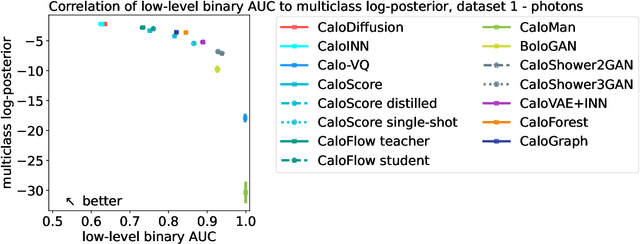
We present the results of the "Fast Calorimeter Simulation Challenge 2022" - the CaloChallenge. We study state-of-the-art generative models on four calorimeter shower datasets of increasing dimensionality, ranging from a few hundred voxels to a few tens of thousand voxels. The 31 individual submissions span a wide range of current popular generative architectures, including Variational AutoEncoders (VAEs), Generative Adversarial Networks (GANs), Normalizing Flows, Diffusion models, and models based on Conditional Flow Matching. We compare all submissions in terms of quality of generated calorimeter showers, as well as shower generation time and model size. To assess the quality we use a broad range of different metrics including differences in 1-dimensional histograms of observables, KPD/FPD scores, AUCs of binary classifiers, and the log-posterior of a multiclass classifier. The results of the CaloChallenge provide the most complete and comprehensive survey of cutting-edge approaches to calorimeter fast simulation to date. In addition, our work provides a uniquely detailed perspective on the important problem of how to evaluate generative models. As such, the results presented here should be applicable for other domains that use generative AI and require fast and faithful generation of samples in a large phase space.

Cascading Failure Prediction via Causal Inference

Causal inference provides an analytical framework to identify and quantify cause-and-effect relationships among a network of interacting agents. This paper offers a novel framework for analyzing cascading failures in power transmission networks. This framework generates a directed latent graph in which the nodes represent the transmission lines and the directed edges encode the cause-effect relationships. This graph has a structure distinct from the system's topology, signifying the intricate fact that both local and non-local interdependencies exist among transmission lines, which are more general than only the local interdependencies that topological graphs can present. This paper formalizes a causal inference framework for predicting how an emerging anomaly propagates throughout the system. Using this framework, two algorithms are designed, providing an analytical framework to identify the most likely and most costly cascading scenarios. The framework's effectiveness is evaluated compared to the pertinent literature on the IEEE 14-bus, 39-bus, and 118-bus systems.

A 3D super-resolution of wind fields via physics-informed pixel-wise self-attention generative adversarial network

To mitigate global warming, greenhouse gas sources need to be resolved at a high spatial resolution and monitored in time to ensure the reduction and ultimately elimination of the pollution source. However, the complexity of computation in resolving high-resolution wind fields left the simulations impractical to test different time lengths and model configurations. This study presents a preliminary development of a physics-informed super-resolution (SR) generative adversarial network (GAN) that super-resolves the three-dimensional (3D) low-resolution wind fields by upscaling x9 times. We develop a pixel-wise self-attention (PWA) module that learns 3D weather dynamics via a self-attention computation followed by a 2D convolution. We also employ a loss term that regularizes the self-attention map during pretraining, capturing the vertical convection process from input wind data. The new PWA SR-GAN shows the high-fidelity super-resolved 3D wind data, learns a wind structure at the high-frequency domain, and reduces the computational cost of a high-resolution wind simulation by x89.7 times.

A Supervised Contrastive Learning Pretrain-Finetune Approach for Time Series

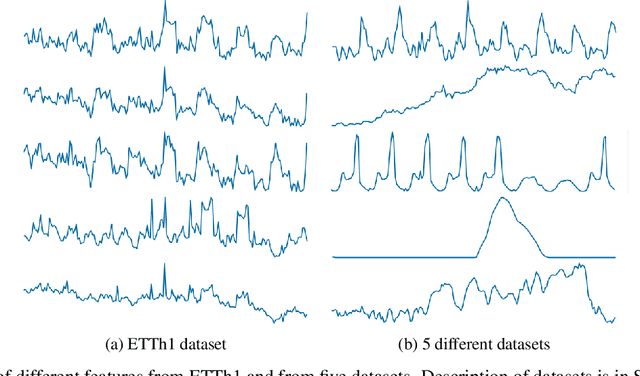
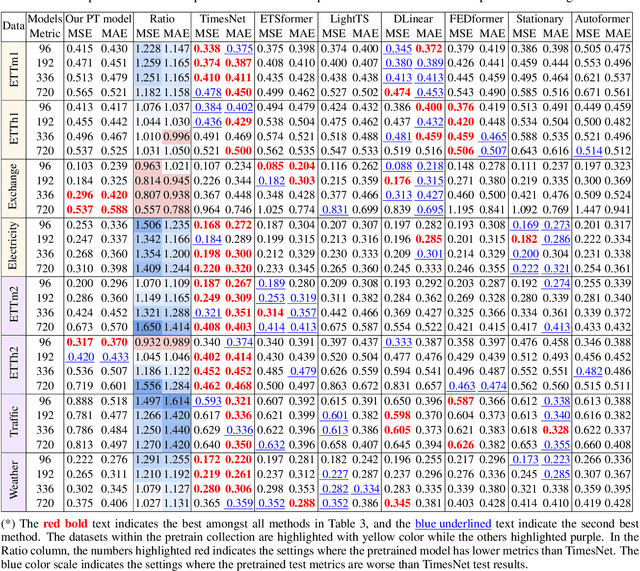
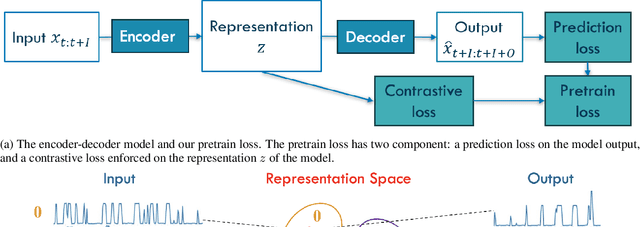
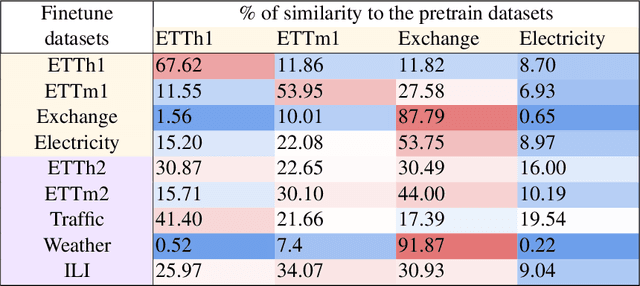
Foundation models have recently gained attention within the field of machine learning thanks to its efficiency in broad data processing. While researchers had attempted to extend this success to time series models, the main challenge is effectively extracting representations and transferring knowledge from pretraining datasets to the target finetuning dataset. To tackle this issue, we introduce a novel pretraining procedure that leverages supervised contrastive learning to distinguish features within each pretraining dataset. This pretraining phase enables a probabilistic similarity metric, which assesses the likelihood of a univariate sample being closely related to one of the pretraining datasets. Subsequently, using this similarity metric as a guide, we propose a fine-tuning procedure designed to enhance the accurate prediction of the target data by aligning it more closely with the learned dynamics of the pretraining datasets. Our experiments have shown promising results which demonstrate the efficacy of our approach.

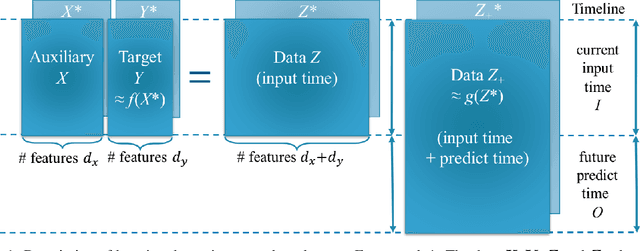
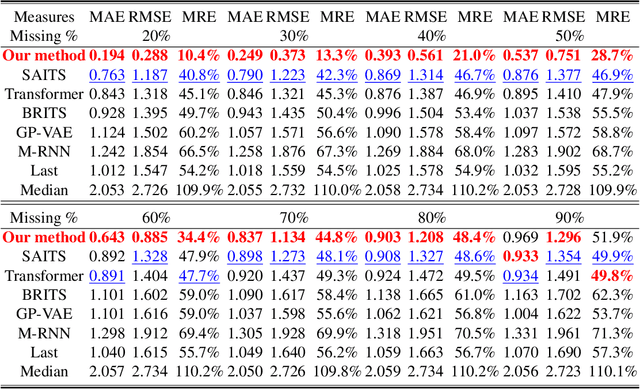
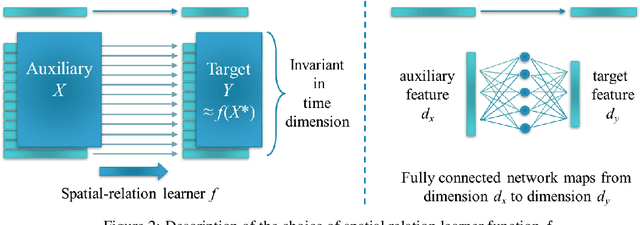
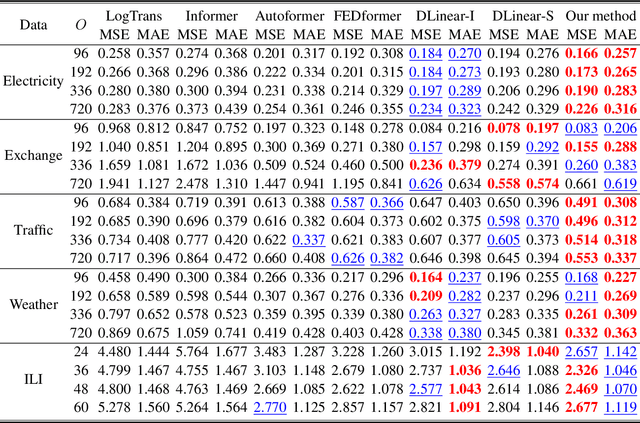
An End-to-End Time Series Model for Simultaneous Imputation and Forecast

Time series forecasting using historical data has been an interesting and challenging topic, especially when the data is corrupted by missing values. In many industrial problem, it is important to learn the inference function between the auxiliary observations and target variables as it provides additional knowledge when the data is not fully observed. We develop an end-to-end time series model that aims to learn the such inference relation and make a multiple-step ahead forecast. Our framework trains jointly two neural networks, one to learn the feature-wise correlations and the other for the modeling of temporal behaviors. Our model is capable of simultaneously imputing the missing entries and making a multiple-step ahead prediction. The experiments show good overall performance of our framework over existing methods in both imputation and forecasting tasks.

Inverse Models for Estimating the Initial Condition of Spatio-Temporal Advection-Diffusion Processes

Inverse problems involve making inference about unknown parameters of a physical process using observational data. This paper investigates an important class of inverse problems -- the estimation of the initial condition of a spatio-temporal advection-diffusion process using spatially sparse data streams. Three spatial sampling schemes are considered, including irregular, non-uniform and shifted uniform sampling. The irregular sampling scheme is the general scenario, while computationally efficient solutions are available in the spectral domain for non-uniform and shifted uniform sampling. For each sampling scheme, the inverse problem is formulated as a regularized convex optimization problem that minimizes the distance between forward model outputs and observations. The optimization problem is solved by the Alternating Direction Method of Multipliers algorithm, which also handles the situation when a linear inequality constraint (e.g., non-negativity) is imposed on the model output. Numerical examples are presented, code is made available on GitHub, and discussions are provided to generate some useful insights of the proposed inverse modeling approaches.

Multi-task Learning for Source Attribution and Field Reconstruction for Methane Monitoring

Inferring the source information of greenhouse gases, such as methane, from spatially sparse sensor observations is an essential element in mitigating climate change. While it is well understood that the complex behavior of the atmospheric dispersion of such pollutants is governed by the Advection-Diffusion equation, it is difficult to directly apply the governing equations to identify the source location and magnitude (inverse problem) because of the spatially sparse and noisy observations, i.e., the pollution concentration is known only at the sensor locations and sensors sensitivity is limited. Here, we develop a multi-task learning framework that can provide high-fidelity reconstruction of the concentration field and identify emission characteristics of the pollution sources such as their location, emission strength, etc. from sparse sensor observations. We demonstrate that our proposed framework is able to achieve accurate reconstruction of the methane concentrations from sparse sensor measurements as well as precisely pin-point the location and emission strength of these pollution sources.

Super Resolution for Turbulent Flows in 2D: Stabilized Physics Informed Neural Networks

We propose a new design of a neural network for solving a zero shot super resolution problem for turbulent flows. We embed Luenberger-type observer into the network's architecture to inform the network of the physics of the process, and to provide error correction and stabilization mechanisms. In addition, to compensate for decrease of observer's performance due to the presence of unknown destabilizing forcing, the network is designed to estimate the contribution of the unknown forcing implicitly from the data over the course of training. By running a set of numerical experiments, we demonstrate that the proposed network does recover unknown forcing from data and is capable of predicting turbulent flows in high resolution from low resolution noisy observations.

S3RP: Self-Supervised Super-Resolution and Prediction for Advection-Diffusion Process

We present a super-resolution model for an advection-diffusion process with limited information. While most of the super-resolution models assume high-resolution (HR) ground-truth data in the training, in many cases such HR dataset is not readily accessible. Here, we show that a Recurrent Convolutional Network trained with physics-based regularizations is able to reconstruct the HR information without having the HR ground-truth data. Moreover, considering the ill-posed nature of a super-resolution problem, we employ the Recurrent Wasserstein Autoencoder to model the uncertainty.

Generative Adversarial Network for Probabilistic Forecast of Random Dynamical System

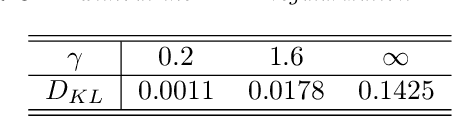
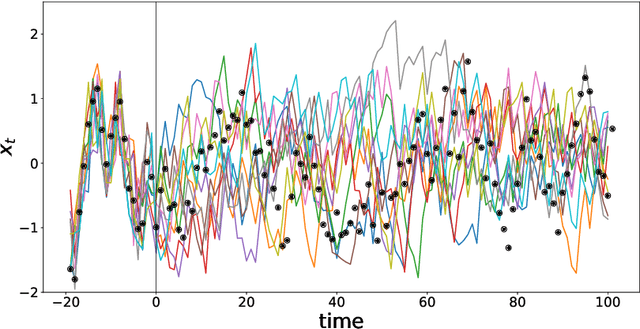
We present a deep learning model for data-driven simulations of random dynamical systems without a distributional assumption. The deep learning model consists of a recurrent neural network, which aims to learn the time marching structure, and a generative adversarial network to learn and sample from the probability distribution of the random dynamical system. Although generative adversarial networks provide a powerful tool to model a complex probability distribution, the training often fails without a proper regularization. Here, we propose a regularization strategy for a generative adversarial network based on consistency conditions for the sequential inference problems. First, the maximum mean discrepancy (MMD) is used to enforce the consistency between conditional and marginal distributions of a stochastic process. Then, the marginal distributions of the multiple-step predictions are regularized by using MMD or from multiple discriminators. The behavior of the proposed model is studied by using three stochastic processes with complex noise structures.