Generative Adversarial Network for Probabilistic Forecast of Random Dynamical System

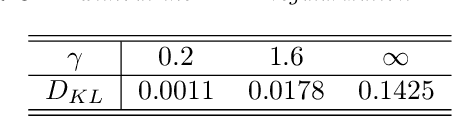
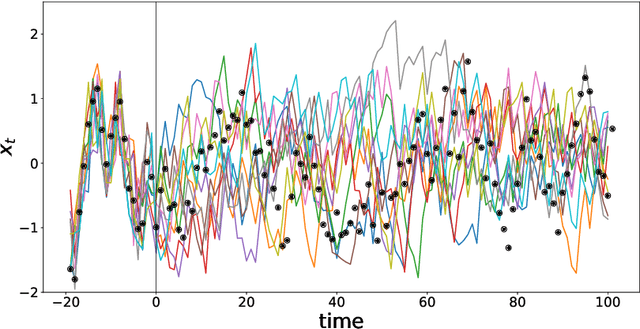
We present a deep learning model for data-driven simulations of random dynamical systems without a distributional assumption. The deep learning model consists of a recurrent neural network, which aims to learn the time marching structure, and a generative adversarial network to learn and sample from the probability distribution of the random dynamical system. Although generative adversarial networks provide a powerful tool to model a complex probability distribution, the training often fails without a proper regularization. Here, we propose a regularization strategy for a generative adversarial network based on consistency conditions for the sequential inference problems. First, the maximum mean discrepancy (MMD) is used to enforce the consistency between conditional and marginal distributions of a stochastic process. Then, the marginal distributions of the multiple-step predictions are regularized by using MMD or from multiple discriminators. The behavior of the proposed model is studied by using three stochastic processes with complex noise structures.