Hiva Ghanbari
Novel and Efficient Approximations for Zero-One Loss of Linear Classifiers
Feb 28, 2019
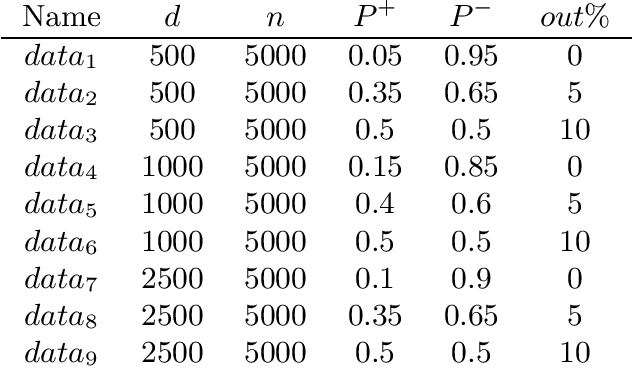

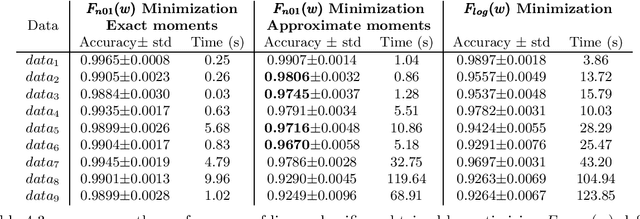
Abstract:The predictive quality of machine learning models is typically measured in terms of their (approximate) expected prediction accuracy or the so-called Area Under the Curve (AUC). Minimizing the reciprocals of these measures are the goals of supervised learning. However, when the models are constructed by the means of empirical risk minimization (ERM), surrogate functions such as the logistic loss or hinge loss are optimized instead. In this work, we show that in the case of linear predictors, the expected error and the expected ranking loss can be effectively approximated by smooth functions whose closed form expressions and those of their first (and second) order derivatives depend on the first and second moments of the data distribution, which can be precomputed. Hence, the complexity of an optimization algorithm applied to these functions does not depend on the size of the training data. These approximation functions are derived under the assumption that the output of the linear classifier for a given data set has an approximately normal distribution. We argue that this assumption is significantly weaker than the Gaussian assumption on the data itself and we support this claim by demonstrating that our new approximation is quite accurate on data sets that are not necessarily Gaussian. We present computational results that show that our proposed approximations and related optimization algorithms can produce linear classifiers with similar or better test accuracy or AUC, than those obtained using state-of-the-art approaches, in a fraction of the time.
Directly and Efficiently Optimizing Prediction Error and AUC of Linear Classifiers
Feb 07, 2018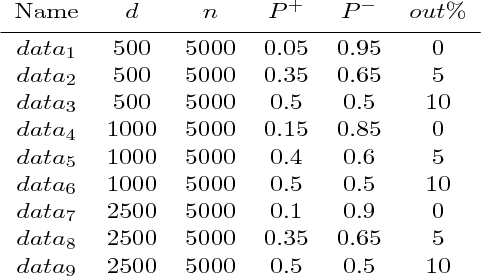
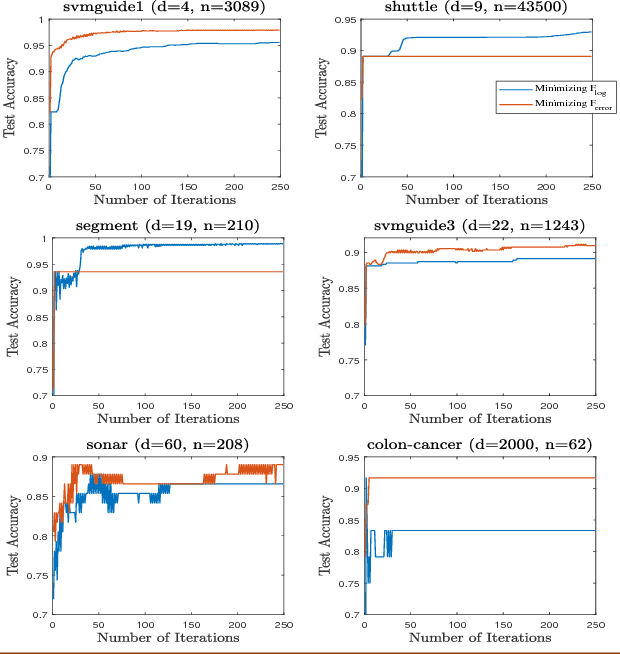
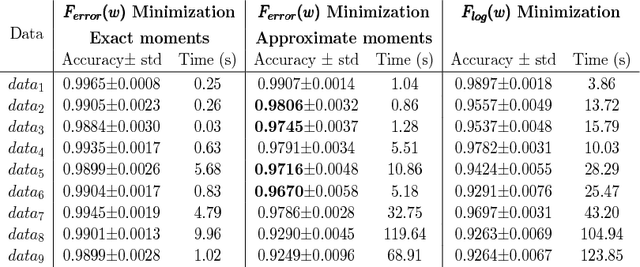
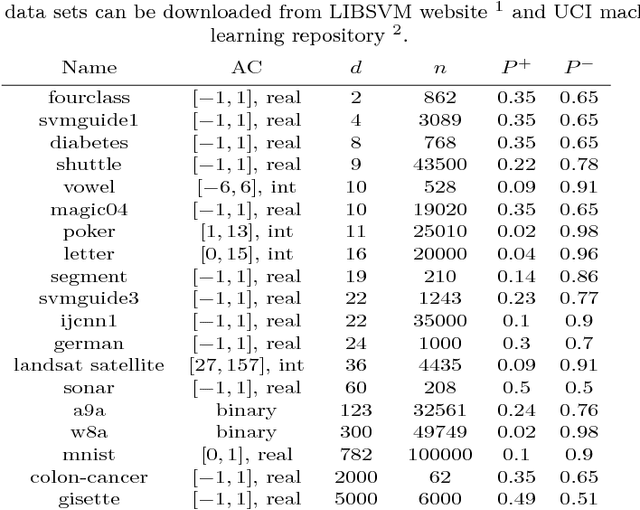
Abstract:The predictive quality of machine learning models is typically measured in terms of their (approximate) expected prediction error or the so-called Area Under the Curve (AUC) for a particular data distribution. However, when the models are constructed by the means of empirical risk minimization, surrogate functions such as the logistic loss are optimized instead. This is done because the empirical approximations of the expected error and AUC functions are nonconvex and nonsmooth, and more importantly have zero derivative almost everywhere. In this work, we show that in the case of linear predictors, and under the assumption that the data has normal distribution, the expected error and the expected AUC are not only smooth, but have closed form expressions, which depend on the first and second moments of the normal distribution. Hence, we derive derivatives of these two functions and use these derivatives in an optimization algorithm to directly optimize the expected error and the AUC. In the case of real data sets, the derivatives can be approximated using empirical moments. We show that even when data is not normally distributed, computed derivatives are sufficiently useful to render an efficient optimization method and high quality solutions. Thus, we propose a gradient-based optimization method for direct optimization of the prediction error and AUC. Moreover, the per-iteration complexity of the proposed algorithm has no dependence on the size of the data set, unlike those for optimizing logistic regression and all other well known empirical risk minimization problems.
Proximal Quasi-Newton Methods for Regularized Convex Optimization with Linear and Accelerated Sublinear Convergence Rates
Oct 17, 2017
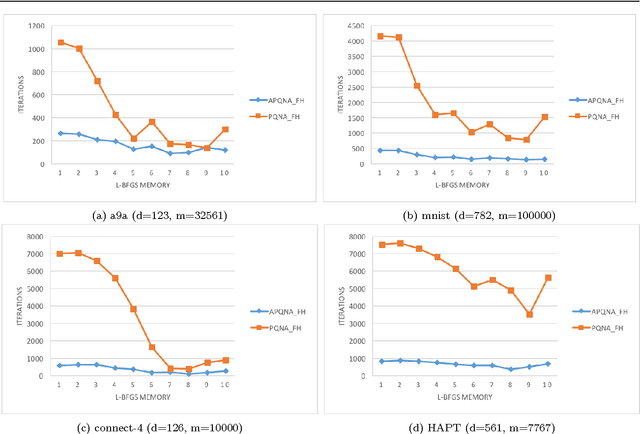
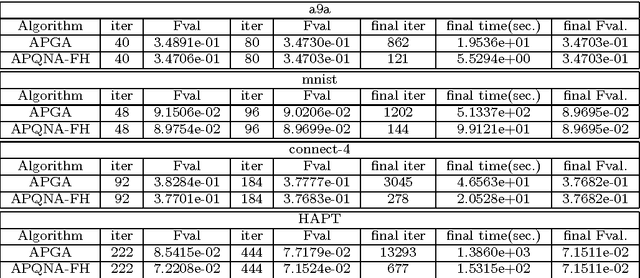
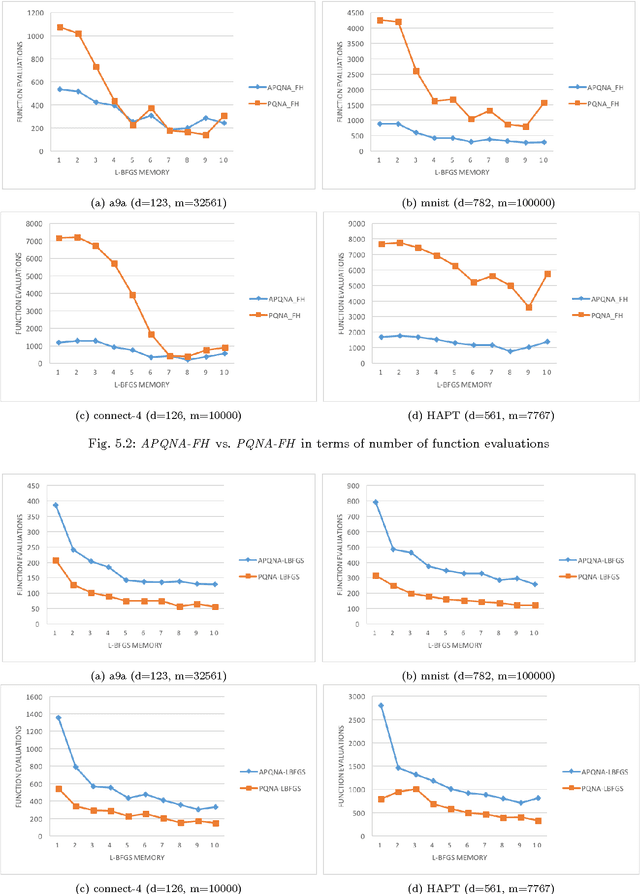
Abstract:In [19], a general, inexact, efficient proximal quasi-Newton algorithm for composite optimization problems has been proposed and a sublinear global convergence rate has been established. In this paper, we analyze the convergence properties of this method, both in the exact and inexact setting, in the case when the objective function is strongly convex. We also investigate a practical variant of this method by establishing a simple stopping criterion for the subproblem optimization. Furthermore, we consider an accelerated variant, based on FISTA [1], to the proximal quasi-Newton algorithm. A similar accelerated method has been considered in [7], where the convergence rate analysis relies on very strong impractical assumptions. We present a modified analysis while relaxing these assumptions and perform a practical comparison of the accelerated proximal quasi- Newton algorithm and the regular one. Our analysis and computational results show that acceleration may not bring any benefit in the quasi-Newton setting.
Black-Box Optimization in Machine Learning with Trust Region Based Derivative Free Algorithm
Mar 20, 2017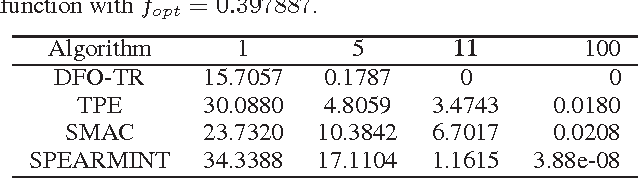
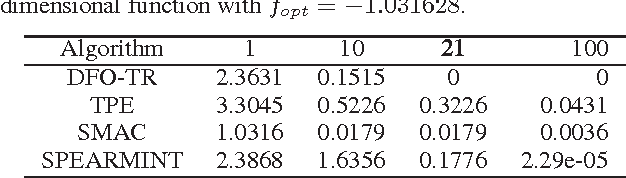
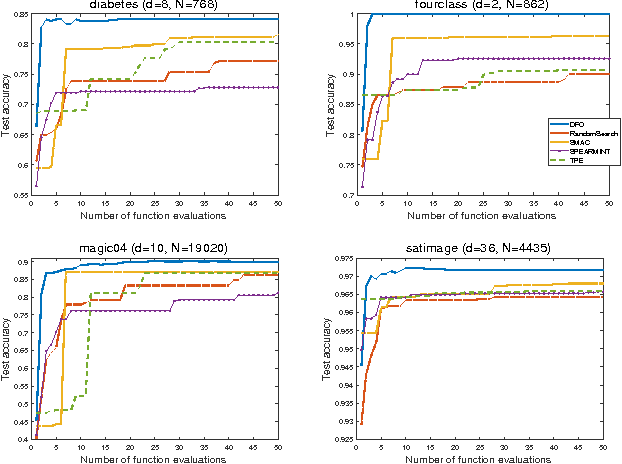
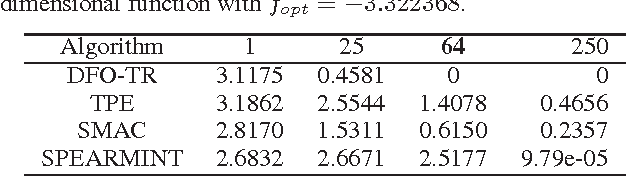
Abstract:In this work, we utilize a Trust Region based Derivative Free Optimization (DFO-TR) method to directly maximize the Area Under Receiver Operating Characteristic Curve (AUC), which is a nonsmooth, noisy function. We show that AUC is a smooth function, in expectation, if the distributions of the positive and negative data points obey a jointly normal distribution. The practical performance of this algorithm is compared to three prominent Bayesian optimization methods and random search. The presented numerical results show that DFO-TR surpasses Bayesian optimization and random search on various black-box optimization problem, such as maximizing AUC and hyperparameter tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge