Proximal Quasi-Newton Methods for Regularized Convex Optimization with Linear and Accelerated Sublinear Convergence Rates
Paper and Code
Oct 17, 2017
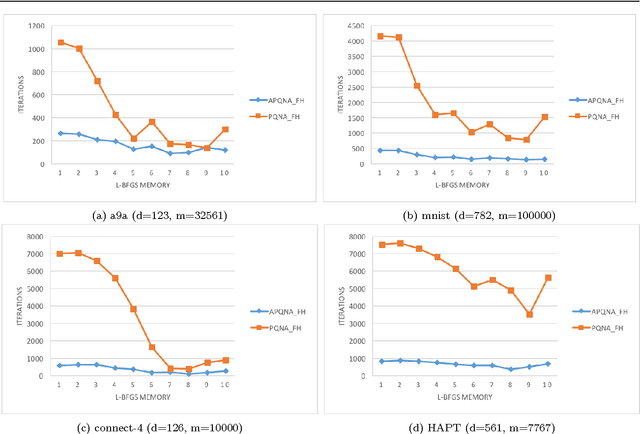
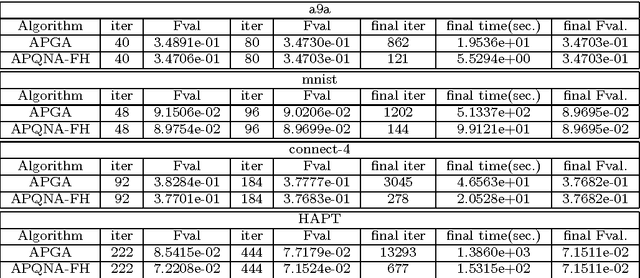
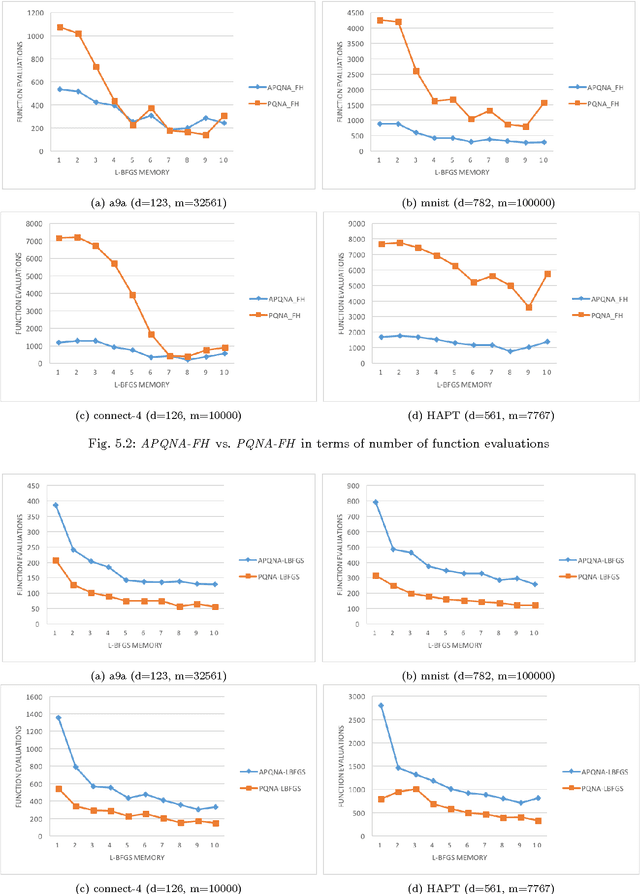
In [19], a general, inexact, efficient proximal quasi-Newton algorithm for composite optimization problems has been proposed and a sublinear global convergence rate has been established. In this paper, we analyze the convergence properties of this method, both in the exact and inexact setting, in the case when the objective function is strongly convex. We also investigate a practical variant of this method by establishing a simple stopping criterion for the subproblem optimization. Furthermore, we consider an accelerated variant, based on FISTA [1], to the proximal quasi-Newton algorithm. A similar accelerated method has been considered in [7], where the convergence rate analysis relies on very strong impractical assumptions. We present a modified analysis while relaxing these assumptions and perform a practical comparison of the accelerated proximal quasi- Newton algorithm and the regular one. Our analysis and computational results show that acceleration may not bring any benefit in the quasi-Newton setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge