Directly and Efficiently Optimizing Prediction Error and AUC of Linear Classifiers

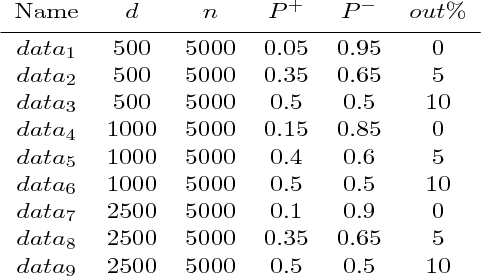
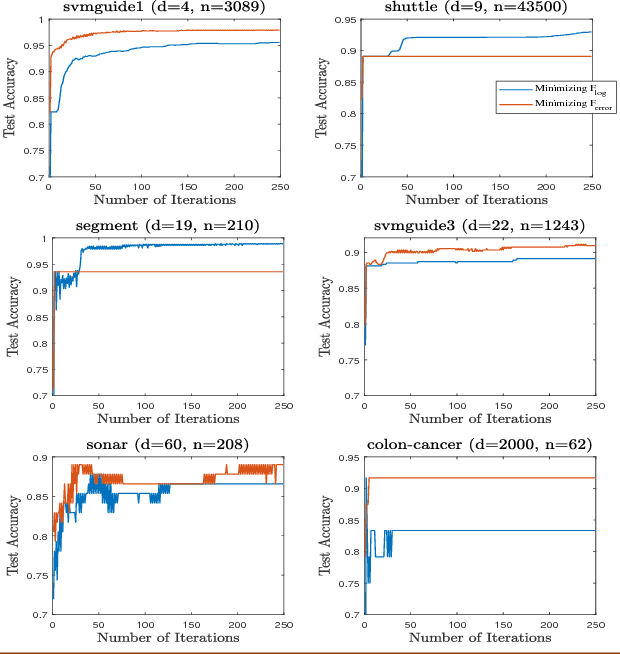
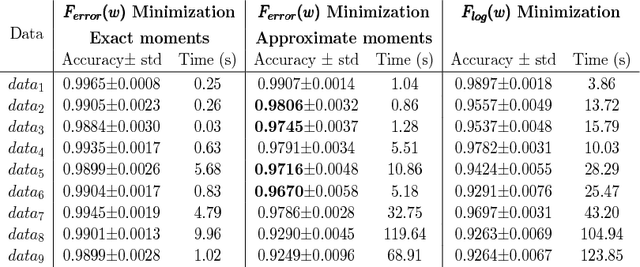
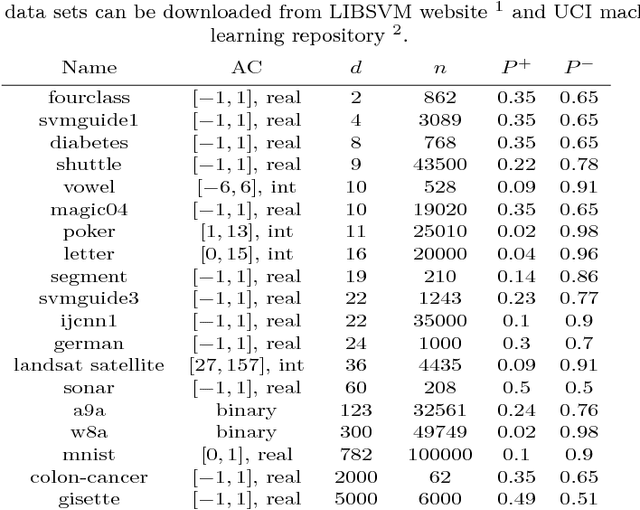
The predictive quality of machine learning models is typically measured in terms of their (approximate) expected prediction error or the so-called Area Under the Curve (AUC) for a particular data distribution. However, when the models are constructed by the means of empirical risk minimization, surrogate functions such as the logistic loss are optimized instead. This is done because the empirical approximations of the expected error and AUC functions are nonconvex and nonsmooth, and more importantly have zero derivative almost everywhere. In this work, we show that in the case of linear predictors, and under the assumption that the data has normal distribution, the expected error and the expected AUC are not only smooth, but have closed form expressions, which depend on the first and second moments of the normal distribution. Hence, we derive derivatives of these two functions and use these derivatives in an optimization algorithm to directly optimize the expected error and the AUC. In the case of real data sets, the derivatives can be approximated using empirical moments. We show that even when data is not normally distributed, computed derivatives are sufficiently useful to render an efficient optimization method and high quality solutions. Thus, we propose a gradient-based optimization method for direct optimization of the prediction error and AUC. Moreover, the per-iteration complexity of the proposed algorithm has no dependence on the size of the data set, unlike those for optimizing logistic regression and all other well known empirical risk minimization problems.