Exact Recovery Guarantees for Parameterized Non-linear System Identification Problem under Adversarial Attacks

In this work, we study the system identification problem for parameterized non-linear systems using basis functions under adversarial attacks. Motivated by the LASSO-type estimators, we analyze the exact recovery property of a non-smooth estimator, which is generated by solving an embedded $\ell_1$-loss minimization problem. First, we derive necessary and sufficient conditions for the well-specifiedness of the estimator and the uniqueness of global solutions to the underlying optimization problem. Next, we provide exact recovery guarantees for the estimator under two different scenarios of boundedness and Lipschitz continuity of the basis functions. The non-asymptotic exact recovery is guaranteed with high probability, even when there are more severely corrupted data than clean data. Finally, we numerically illustrate the validity of our theory. This is the first study on the sample complexity analysis of a non-smooth estimator for the non-linear system identification problem.

Factorization Approach for Low-complexity Matrix Completion Problems: Exponential Number of Spurious Solutions and Failure of Gradient Methods

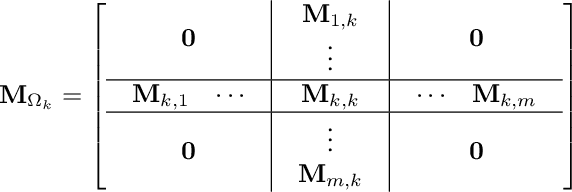
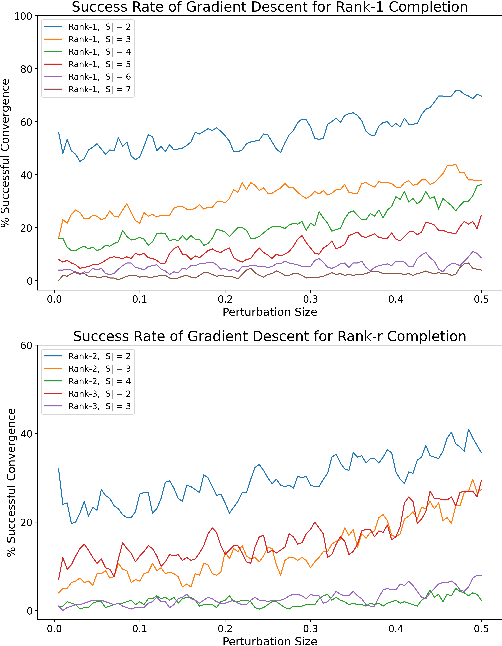
It is well-known that the Burer-Monteiro (B-M) factorization approach can efficiently solve low-rank matrix optimization problems under the RIP condition. It is natural to ask whether B-M factorization-based methods can succeed on any low-rank matrix optimization problems with a low information-theoretic complexity, i.e., polynomial-time solvable problems that have a unique solution. In this work, we provide a negative answer to the above question. We investigate the landscape of B-M factorized polynomial-time solvable matrix completion (MC) problems, which are the most popular subclass of low-rank matrix optimization problems without the RIP condition. We construct an instance of polynomial-time solvable MC problems with exponentially many spurious local minima, which leads to the failure of most gradient-based methods. Based on those results, we define a new complexity metric that potentially measures the solvability of low-rank matrix optimization problems based on the B-M factorization approach. In addition, we show that more measurements of the ground truth matrix can deteriorate the landscape, which further reveals the unfavorable behavior of the B-M factorization on general low-rank matrix optimization problems.

A Mathematical Foundation for Robust Machine Learning based on Bias-Variance Trade-off

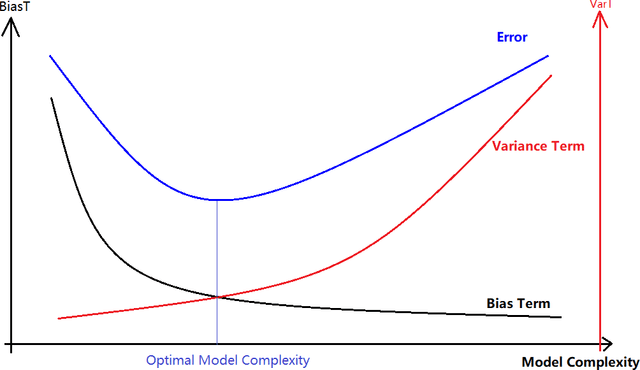
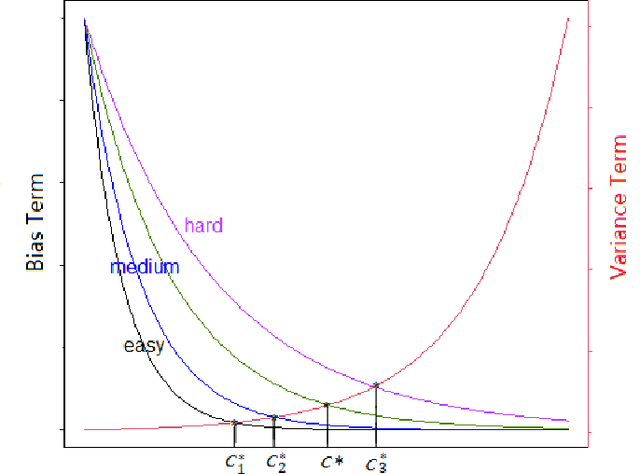
A common assumption in machine learning is that samples are independently and identically distributed (i.i.d). However, the contributions of different samples are not identical in training. Some samples are difficult to learn and some samples are noisy. The unequal contributions of samples has a considerable effect on training performances. Studies focusing on unequal sample contributions (e.g., easy, hard, noisy) in learning usually refer to these contributions as robust machine learning (RML). Weighing and regularization are two common techniques in RML. Numerous learning algorithms have been proposed but the strategies for dealing with easy/hard/noisy samples differ or even contradict with different learning algorithms. For example, some strategies take the hard samples first, whereas some strategies take easy first. Conducting a clear comparison for existing RML algorithms in dealing with different samples is difficult due to lack of a unified theoretical framework for RML. This study attempts to construct a mathematical foundation for RML based on the bias-variance trade-off theory. A series of definitions and properties are presented and proved. Several classical learning algorithms are also explained and compared. Improvements of existing methods are obtained based on the comparison. A unified method that combines two classical learning strategies is proposed.