Tackling the Imbalance for GNNs

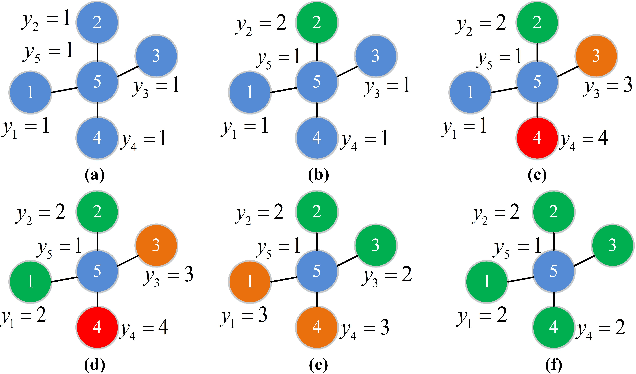
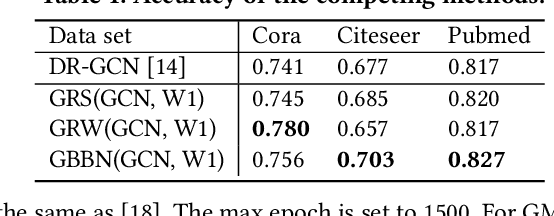
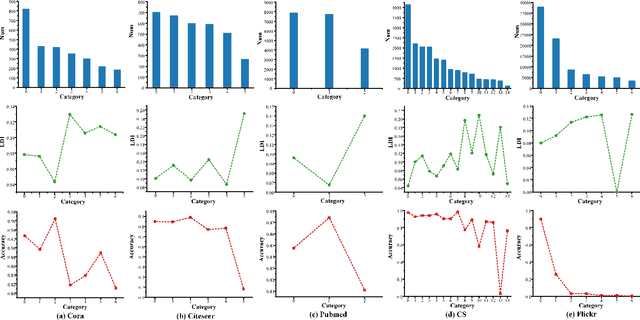
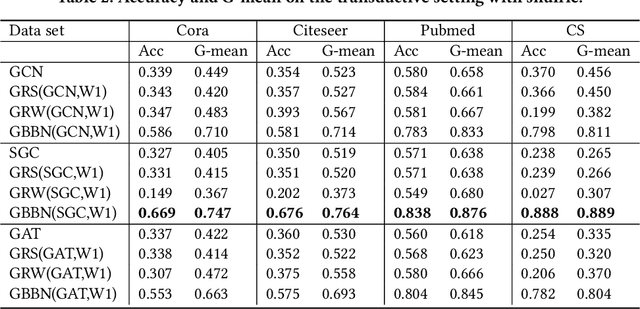
Different from deep neural networks for non-graph data classification, graph neural networks (GNNs) leverage the information exchange between nodes (or samples) when representing nodes. The category distribution shows an imbalance or even a highly-skewed trend on nearly all existing benchmark GNN data sets. The imbalanced distribution will cause misclassification of nodes in the minority classes, and even cause the classification performance on the entire data set to decrease. This study explores the effects of the imbalance problem on the performances of GNNs and proposes new methodologies to solve it. First, a node-level index, namely, the label difference index ($LDI$), is defined to quantitatively analyze the relationship between imbalance and misclassification. The less samples in a class, the higher the value of its average $LDI$; the higher the $LDI$ of a sample, the more likely the sample will be misclassified. We define a new loss and propose four new methods based on $LDI$. Experimental results indicate that the classification accuracies of the three among our proposed four new methods are better in both transductive and inductive settings. The $LDI$ can be applied to other GNNs.

A Mathematical Foundation for Robust Machine Learning based on Bias-Variance Trade-off

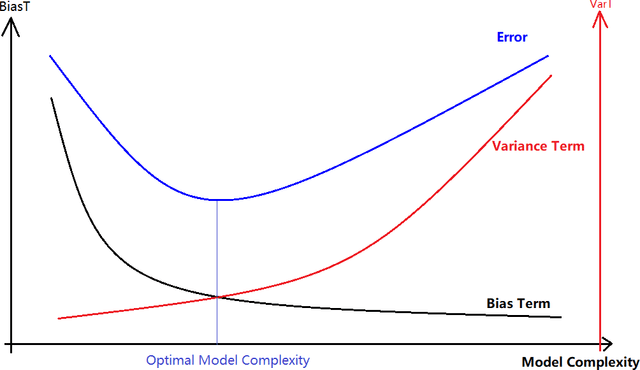
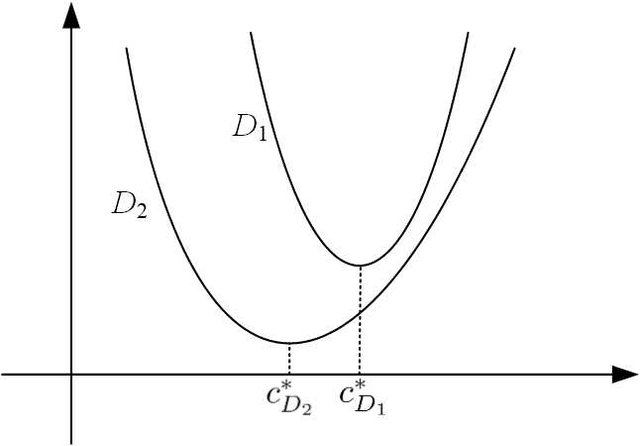
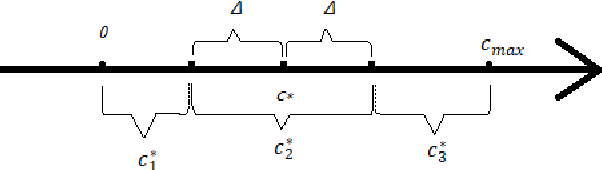
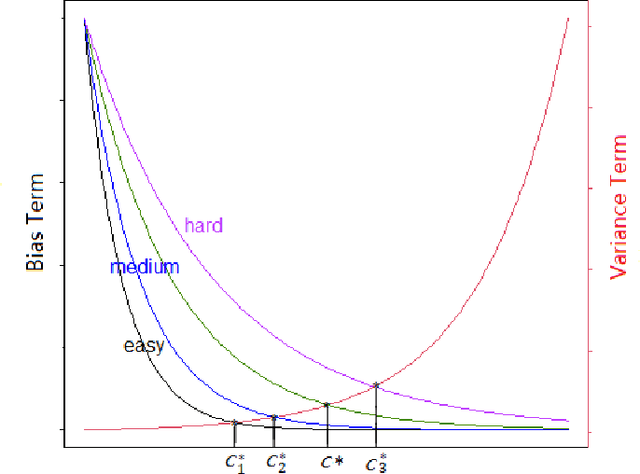
A common assumption in machine learning is that samples are independently and identically distributed (i.i.d). However, the contributions of different samples are not identical in training. Some samples are difficult to learn and some samples are noisy. The unequal contributions of samples has a considerable effect on training performances. Studies focusing on unequal sample contributions (e.g., easy, hard, noisy) in learning usually refer to these contributions as robust machine learning (RML). Weighing and regularization are two common techniques in RML. Numerous learning algorithms have been proposed but the strategies for dealing with easy/hard/noisy samples differ or even contradict with different learning algorithms. For example, some strategies take the hard samples first, whereas some strategies take easy first. Conducting a clear comparison for existing RML algorithms in dealing with different samples is difficult due to lack of a unified theoretical framework for RML. This study attempts to construct a mathematical foundation for RML based on the bias-variance trade-off theory. A series of definitions and properties are presented and proved. Several classical learning algorithms are also explained and compared. Improvements of existing methods are obtained based on the comparison. A unified method that combines two classical learning strategies is proposed.