Is Data Valuation Learnable and Interpretable?

Measuring the value of individual samples is critical for many data-driven tasks, e.g., the training of a deep learning model. Recent literature witnesses the substantial efforts in developing data valuation methods. The primary data valuation methodology is based on the Shapley value from game theory, and various methods are proposed along this path. {Even though Shapley value-based valuation has solid theoretical basis, it is entirely an experiment-based approach and no valuation model has been constructed so far.} In addition, current data valuation methods ignore the interpretability of the output values, despite an interptable data valuation method is of great helpful for applications such as data pricing. This study aims to answer an important question: is data valuation learnable and interpretable? A learned valuation model have several desirable merits such as fixed number of parameters and knowledge reusability. An intrepretable data valuation model can explain why a sample is valuable or invaluable. To this end, two new data value modeling frameworks are proposed, in which a multi-layer perception~(MLP) and a new regression tree are utilized as specific base models for model training and interpretability, respectively. Extensive experiments are conducted on benchmark datasets. {The experimental results provide a positive answer for the question.} Our study opens up a new technical path for the assessing of data values. Large data valuation models can be built across many different data-driven tasks, which can promote the widespread application of data valuation.

Data Valuation by Leveraging Global and Local Statistical Information

Data valuation has garnered increasing attention in recent years, given the critical role of high-quality data in various applications, particularly in machine learning tasks. There are diverse technical avenues to quantify the value of data within a corpus. While Shapley value-based methods are among the most widely used techniques in the literature due to their solid theoretical foundation, the accurate calculation of Shapley values is often intractable, leading to the proposal of numerous approximated calculation methods. Despite significant progress, nearly all existing methods overlook the utilization of distribution information of values within a data corpus. In this paper, we demonstrate that both global and local statistical information of value distributions hold significant potential for data valuation within the context of machine learning. Firstly, we explore the characteristics of both global and local value distributions across several simulated and real data corpora. Useful observations and clues are obtained. Secondly, we propose a new data valuation method that estimates Shapley values by incorporating the explored distribution characteristics into an existing method, AME. Thirdly, we present a new path to address the dynamic data valuation problem by formulating an optimization problem that integrates information of both global and local value distributions. Extensive experiments are conducted on Shapley value estimation, value-based data removal/adding, mislabeled data detection, and incremental/decremental data valuation. The results showcase the effectiveness and efficiency of our proposed methodologies, affirming the significant potential of global and local value distributions in data valuation.

Data Optimization in Deep Learning: A Survey

Large-scale, high-quality data are considered an essential factor for the successful application of many deep learning techniques. Meanwhile, numerous real-world deep learning tasks still have to contend with the lack of sufficient amounts of high-quality data. Additionally, issues such as model robustness, fairness, and trustworthiness are also closely related to training data. Consequently, a huge number of studies in the existing literature have focused on the data aspect in deep learning tasks. Some typical data optimization techniques include data augmentation, logit perturbation, sample weighting, and data condensation. These techniques usually come from different deep learning divisions and their theoretical inspirations or heuristic motivations may seem unrelated to each other. This study aims to organize a wide range of existing data optimization methodologies for deep learning from the previous literature, and makes the effort to construct a comprehensive taxonomy for them. The constructed taxonomy considers the diversity of split dimensions, and deep sub-taxonomies are constructed for each dimension. On the basis of the taxonomy, connections among the extensive data optimization methods for deep learning are built in terms of four aspects. We probe into rendering several promising and interesting future directions. The constructed taxonomy and the revealed connections will enlighten the better understanding of existing methods and the design of novel data optimization techniques. Furthermore, our aspiration for this survey is to promote data optimization as an independent subdivision of deep learning. A curated, up-to-date list of resources related to data optimization in deep learning is available at \url{https://github.com/YaoRujing/Data-Optimization}.

Rethinking Class Imbalance in Machine Learning

Imbalance learning is a subfield of machine learning that focuses on learning tasks in the presence of class imbalance. Nearly all existing studies refer to class imbalance as a proportion imbalance, where the proportion of training samples in each class is not balanced. The ignorance of the proportion imbalance will result in unfairness between/among classes and poor generalization capability. Previous literature has presented numerous methods for either theoretical/empirical analysis or new methods for imbalance learning. This study presents a new taxonomy of class imbalance in machine learning with a broader scope. Four other types of imbalance, namely, variance, distance, neighborhood, and quality imbalances between/among classes, which may exist in machine learning tasks, are summarized. Two different levels of imbalance including global and local are also presented. Theoretical analysis is used to illustrate the significant impact of the new imbalance types on learning fairness. Moreover, our taxonomy and theoretical conclusions are used to analyze the shortcomings of several classical methods. As an example, we propose a new logit perturbation-based imbalance learning loss when proportion, variance, and distance imbalances exist simultaneously. Several classical losses become the special case of our proposed method. Meta learning is utilized to infer the hyper-parameters related to the three types of imbalance. Experimental results on several benchmark corpora validate the effectiveness of the proposed method.

Implicit Counterfactual Data Augmentation for Deep Neural Networks

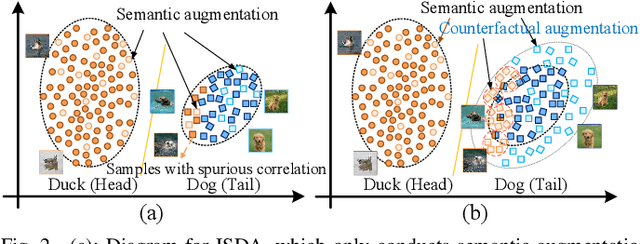
Machine-learning models are prone to capturing the spurious correlations between non-causal attributes and classes, with counterfactual data augmentation being a promising direction for breaking these spurious associations. However, explicitly generating counterfactual data is challenging, with the training efficiency declining. Therefore, this study proposes an implicit counterfactual data augmentation (ICDA) method to remove spurious correlations and make stable predictions. Specifically, first, a novel sample-wise augmentation strategy is developed that generates semantically and counterfactually meaningful deep features with distinct augmentation strength for each sample. Second, we derive an easy-to-compute surrogate loss on the augmented feature set when the number of augmented samples becomes infinite. Third, two concrete schemes are proposed, including direct quantification and meta-learning, to derive the key parameters for the robust loss. In addition, ICDA is explained from a regularization aspect, with extensive experiments indicating that our method consistently improves the generalization performance of popular depth networks on multiple typical learning scenarios that require out-of-distribution generalization.

Combining Adversaries with Anti-adversaries in Training

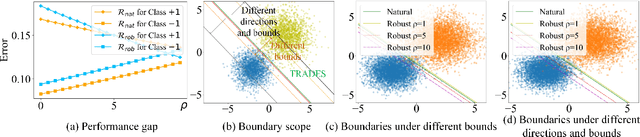
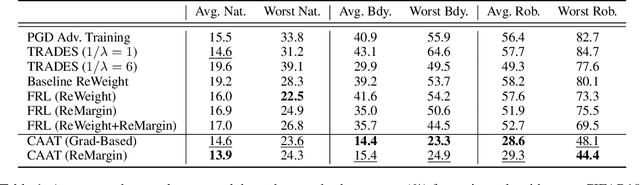
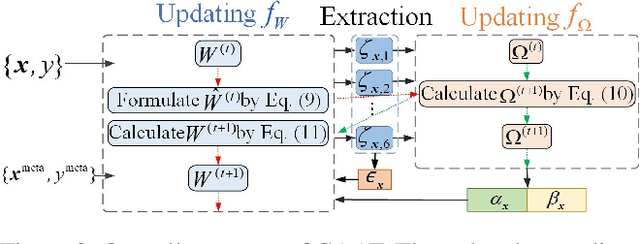
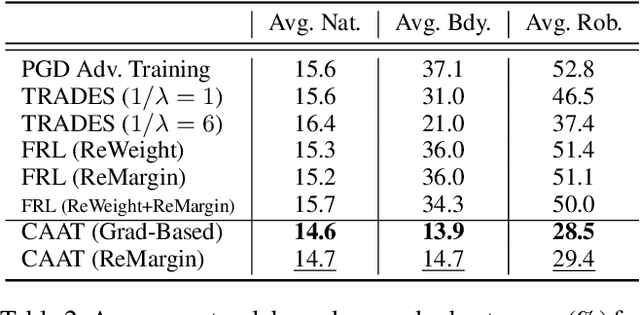
Adversarial training is an effective learning technique to improve the robustness of deep neural networks. In this study, the influence of adversarial training on deep learning models in terms of fairness, robustness, and generalization is theoretically investigated under more general perturbation scope that different samples can have different perturbation directions (the adversarial and anti-adversarial directions) and varied perturbation bounds. Our theoretical explorations suggest that the combination of adversaries and anti-adversaries (samples with anti-adversarial perturbations) in training can be more effective in achieving better fairness between classes and a better tradeoff between robustness and generalization in some typical learning scenarios (e.g., noisy label learning and imbalance learning) compared with standard adversarial training. On the basis of our theoretical findings, a more general learning objective that combines adversaries and anti-adversaries with varied bounds on each training sample is presented. Meta learning is utilized to optimize the combination weights. Experiments on benchmark datasets under different learning scenarios verify our theoretical findings and the effectiveness of the proposed methodology.

Understanding Difficulty-based Sample Weighting with a Universal Difficulty Measure

Sample weighting is widely used in deep learning. A large number of weighting methods essentially utilize the learning difficulty of training samples to calculate their weights. In this study, this scheme is called difficulty-based weighting. Two important issues arise when explaining this scheme. First, a unified difficulty measure that can be theoretically guaranteed for training samples does not exist. The learning difficulties of the samples are determined by multiple factors including noise level, imbalance degree, margin, and uncertainty. Nevertheless, existing measures only consider a single factor or in part, but not in their entirety. Second, a comprehensive theoretical explanation is lacking with respect to demonstrating why difficulty-based weighting schemes are effective in deep learning. In this study, we theoretically prove that the generalization error of a sample can be used as a universal difficulty measure. Furthermore, we provide formal theoretical justifications on the role of difficulty-based weighting for deep learning, consequently revealing its positive influences on both the optimization dynamics and generalization performance of deep models, which is instructive to existing weighting schemes.

Class-Level Logit Perturbation

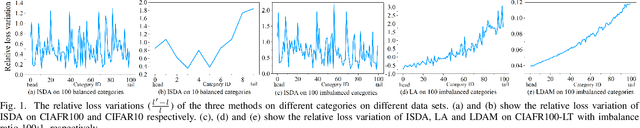
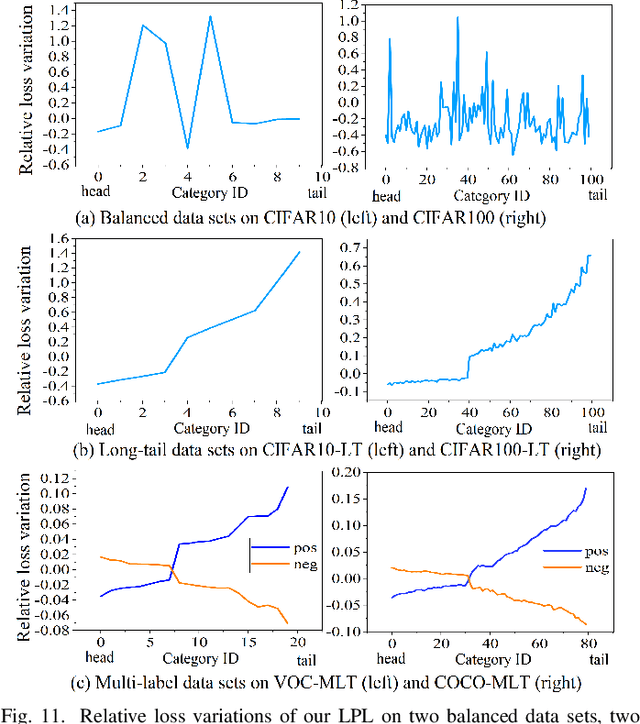
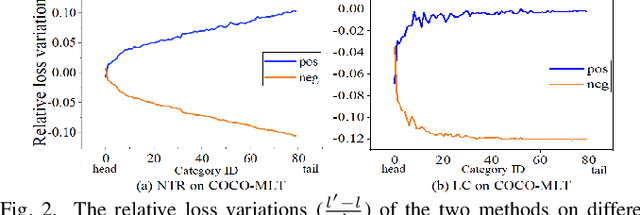
Features, logits, and labels are the three primary data when a sample passes through a deep neural network. Feature perturbation and label perturbation receive increasing attention in recent years. They have been proven to be useful in various deep learning approaches. For example, (adversarial) feature perturbation can improve the robustness or even generalization capability of learned models. However, limited studies have explicitly explored for the perturbation of logit vectors. This work discusses several existing methods related to class-level logit perturbation. A unified viewpoint between positive/negative data augmentation and loss variations incurred by logit perturbation is established. A theoretical analysis is provided to illuminate why class-level logit perturbation is useful. Accordingly, new methodologies are proposed to explicitly learn to perturb logits for both single-label and multi-label classification tasks. Extensive experiments on benchmark image classification data sets and their long-tail versions indicated the competitive performance of our learning method. As it only perturbs on logit, it can be used as a plug-in to fuse with any existing classification algorithms. All the codes are available at https://github.com/limengyang1992/lpl.

Exploring the Learning Difficulty of Data Theory and Measure

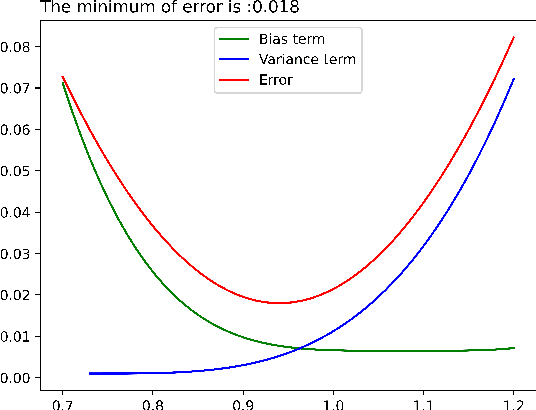
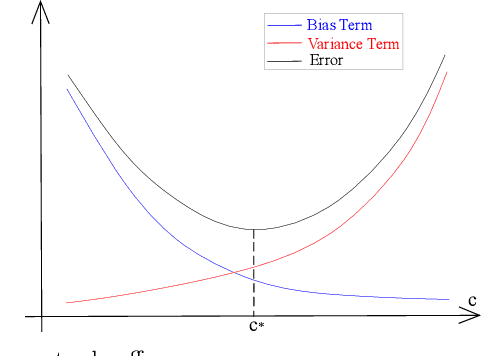
As learning difficulty is crucial for machine learning (e.g., difficulty-based weighting learning strategies), previous literature has proposed a number of learning difficulty measures. However, no comprehensive investigation for learning difficulty is available to date, resulting in that nearly all existing measures are heuristically defined without a rigorous theoretical foundation. In addition, there is no formal definition of easy and hard samples even though they are crucial in many studies. This study attempts to conduct a pilot theoretical study for learning difficulty of samples. First, a theoretical definition of learning difficulty is proposed on the basis of the bias-variance trade-off theory on generalization error. Theoretical definitions of easy and hard samples are established on the basis of the proposed definition. A practical measure of learning difficulty is given as well inspired by the formal definition. Second, the properties for learning difficulty-based weighting strategies are explored. Subsequently, several classical weighting methods in machine learning can be well explained on account of explored properties. Third, the proposed measure is evaluated to verify its reasonability and superiority in terms of several main difficulty factors. The comparison in these experiments indicates that the proposed measure significantly outperforms the other measures throughout the experiments.

Tackling the Imbalance for GNNs

Different from deep neural networks for non-graph data classification, graph neural networks (GNNs) leverage the information exchange between nodes (or samples) when representing nodes. The category distribution shows an imbalance or even a highly-skewed trend on nearly all existing benchmark GNN data sets. The imbalanced distribution will cause misclassification of nodes in the minority classes, and even cause the classification performance on the entire data set to decrease. This study explores the effects of the imbalance problem on the performances of GNNs and proposes new methodologies to solve it. First, a node-level index, namely, the label difference index ($LDI$), is defined to quantitatively analyze the relationship between imbalance and misclassification. The less samples in a class, the higher the value of its average $LDI$; the higher the $LDI$ of a sample, the more likely the sample will be misclassified. We define a new loss and propose four new methods based on $LDI$. Experimental results indicate that the classification accuracies of the three among our proposed four new methods are better in both transductive and inductive settings. The $LDI$ can be applied to other GNNs.