Fengguang Su
Class-Level Logit Perturbation
Sep 26, 2022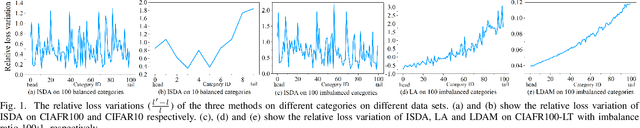

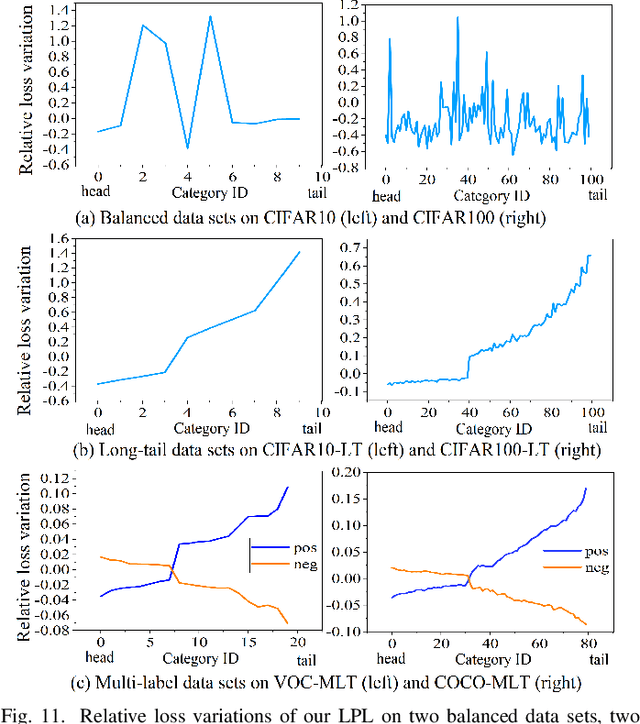
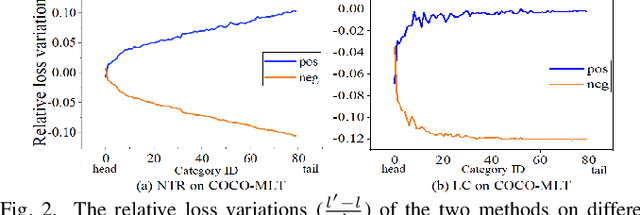
Abstract:Features, logits, and labels are the three primary data when a sample passes through a deep neural network. Feature perturbation and label perturbation receive increasing attention in recent years. They have been proven to be useful in various deep learning approaches. For example, (adversarial) feature perturbation can improve the robustness or even generalization capability of learned models. However, limited studies have explicitly explored for the perturbation of logit vectors. This work discusses several existing methods related to class-level logit perturbation. A unified viewpoint between positive/negative data augmentation and loss variations incurred by logit perturbation is established. A theoretical analysis is provided to illuminate why class-level logit perturbation is useful. Accordingly, new methodologies are proposed to explicitly learn to perturb logits for both single-label and multi-label classification tasks. Extensive experiments on benchmark image classification data sets and their long-tail versions indicated the competitive performance of our learning method. As it only perturbs on logit, it can be used as a plug-in to fuse with any existing classification algorithms. All the codes are available at https://github.com/limengyang1992/lpl.
Exploring the Learning Difficulty of Data Theory and Measure
May 16, 2022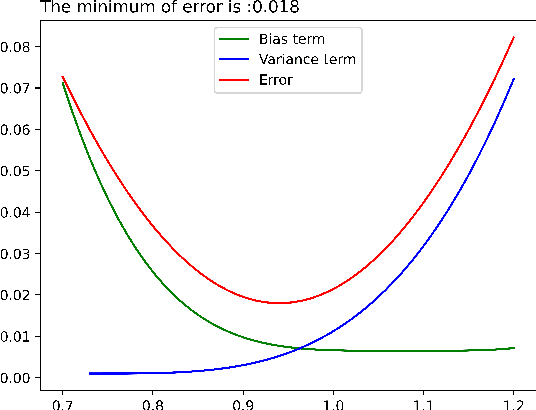
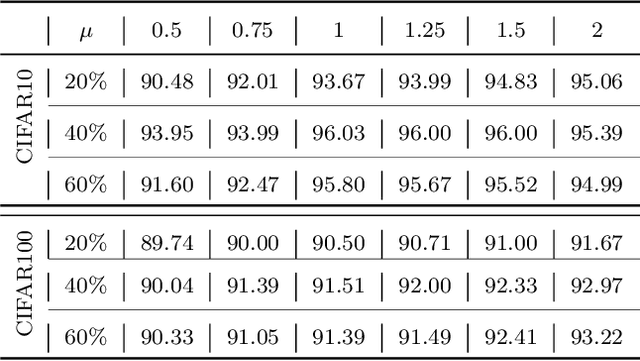
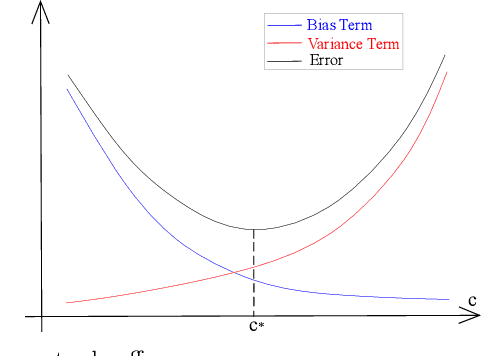

Abstract:As learning difficulty is crucial for machine learning (e.g., difficulty-based weighting learning strategies), previous literature has proposed a number of learning difficulty measures. However, no comprehensive investigation for learning difficulty is available to date, resulting in that nearly all existing measures are heuristically defined without a rigorous theoretical foundation. In addition, there is no formal definition of easy and hard samples even though they are crucial in many studies. This study attempts to conduct a pilot theoretical study for learning difficulty of samples. First, a theoretical definition of learning difficulty is proposed on the basis of the bias-variance trade-off theory on generalization error. Theoretical definitions of easy and hard samples are established on the basis of the proposed definition. A practical measure of learning difficulty is given as well inspired by the formal definition. Second, the properties for learning difficulty-based weighting strategies are explored. Subsequently, several classical weighting methods in machine learning can be well explained on account of explored properties. Third, the proposed measure is evaluated to verify its reasonability and superiority in terms of several main difficulty factors. The comparison in these experiments indicates that the proposed measure significantly outperforms the other measures throughout the experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge