Yingjun Deng
Exploring the Learning Difficulty of Data Theory and Measure
May 16, 2022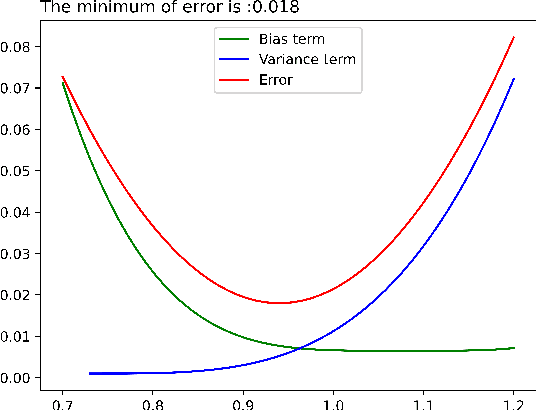
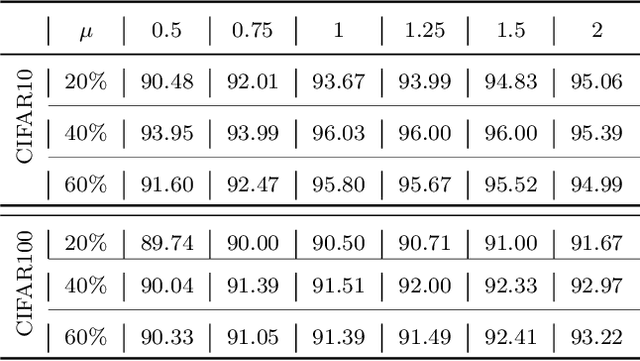

Abstract:As learning difficulty is crucial for machine learning (e.g., difficulty-based weighting learning strategies), previous literature has proposed a number of learning difficulty measures. However, no comprehensive investigation for learning difficulty is available to date, resulting in that nearly all existing measures are heuristically defined without a rigorous theoretical foundation. In addition, there is no formal definition of easy and hard samples even though they are crucial in many studies. This study attempts to conduct a pilot theoretical study for learning difficulty of samples. First, a theoretical definition of learning difficulty is proposed on the basis of the bias-variance trade-off theory on generalization error. Theoretical definitions of easy and hard samples are established on the basis of the proposed definition. A practical measure of learning difficulty is given as well inspired by the formal definition. Second, the properties for learning difficulty-based weighting strategies are explored. Subsequently, several classical weighting methods in machine learning can be well explained on account of explored properties. Third, the proposed measure is evaluated to verify its reasonability and superiority in terms of several main difficulty factors. The comparison in these experiments indicates that the proposed measure significantly outperforms the other measures throughout the experiments.
A Mathematical Foundation for Robust Machine Learning based on Bias-Variance Trade-off
Jun 22, 2021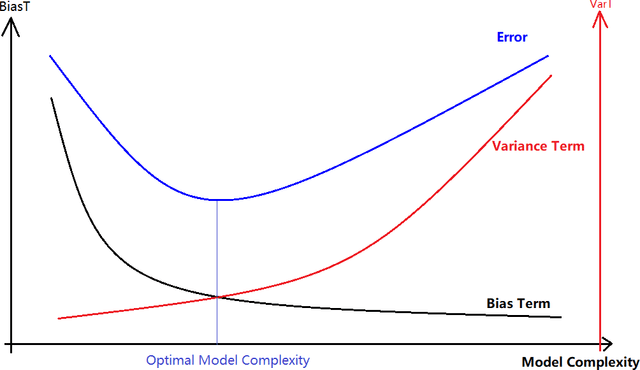
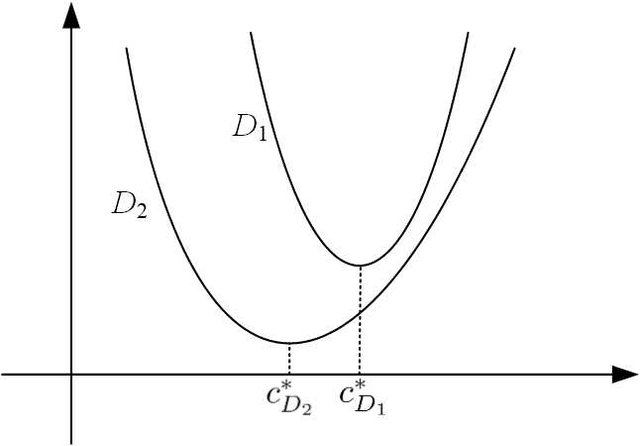
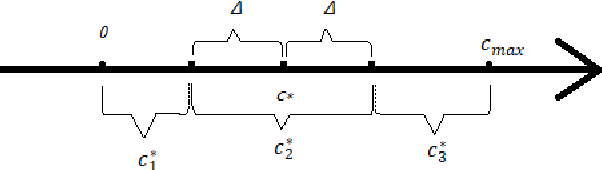
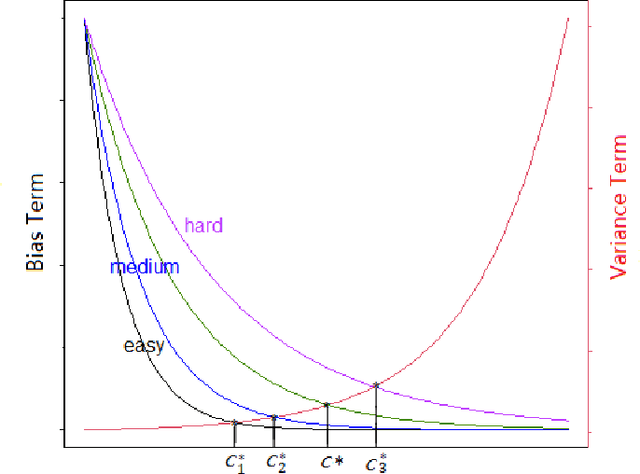
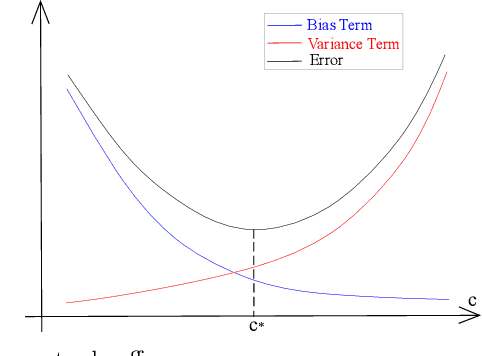
Abstract:A common assumption in machine learning is that samples are independently and identically distributed (i.i.d). However, the contributions of different samples are not identical in training. Some samples are difficult to learn and some samples are noisy. The unequal contributions of samples has a considerable effect on training performances. Studies focusing on unequal sample contributions (e.g., easy, hard, noisy) in learning usually refer to these contributions as robust machine learning (RML). Weighing and regularization are two common techniques in RML. Numerous learning algorithms have been proposed but the strategies for dealing with easy/hard/noisy samples differ or even contradict with different learning algorithms. For example, some strategies take the hard samples first, whereas some strategies take easy first. Conducting a clear comparison for existing RML algorithms in dealing with different samples is difficult due to lack of a unified theoretical framework for RML. This study attempts to construct a mathematical foundation for RML based on the bias-variance trade-off theory. A series of definitions and properties are presented and proved. Several classical learning algorithms are also explained and compared. Improvements of existing methods are obtained based on the comparison. A unified method that combines two classical learning strategies is proposed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge