Enhancing Efficiency of Safe Reinforcement Learning via Sample Manipulation

Safe reinforcement learning (RL) is crucial for deploying RL agents in real-world applications, as it aims to maximize long-term rewards while satisfying safety constraints. However, safe RL often suffers from sample inefficiency, requiring extensive interactions with the environment to learn a safe policy. We propose Efficient Safe Policy Optimization (ESPO), a novel approach that enhances the efficiency of safe RL through sample manipulation. ESPO employs an optimization framework with three modes: maximizing rewards, minimizing costs, and balancing the trade-off between the two. By dynamically adjusting the sampling process based on the observed conflict between reward and safety gradients, ESPO theoretically guarantees convergence, optimization stability, and improved sample complexity bounds. Experiments on the Safety-MuJoCo and Omnisafe benchmarks demonstrate that ESPO significantly outperforms existing primal-based and primal-dual-based baselines in terms of reward maximization and constraint satisfaction. Moreover, ESPO achieves substantial gains in sample efficiency, requiring 25--29% fewer samples than baselines, and reduces training time by 21--38%.

Safe and Balanced: A Framework for Constrained Multi-Objective Reinforcement Learning

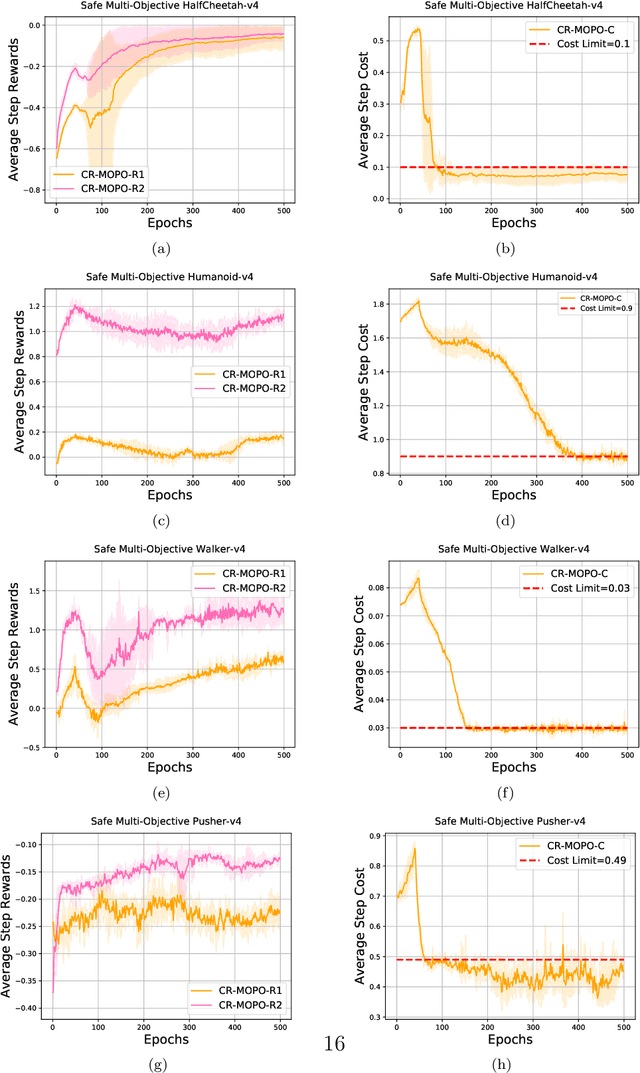
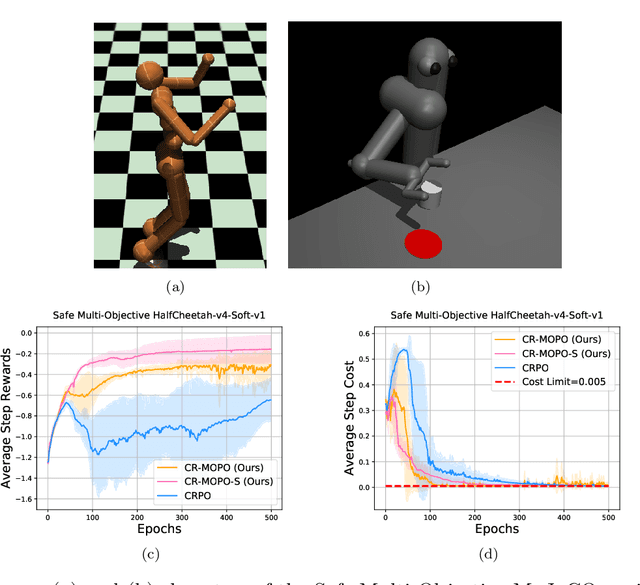
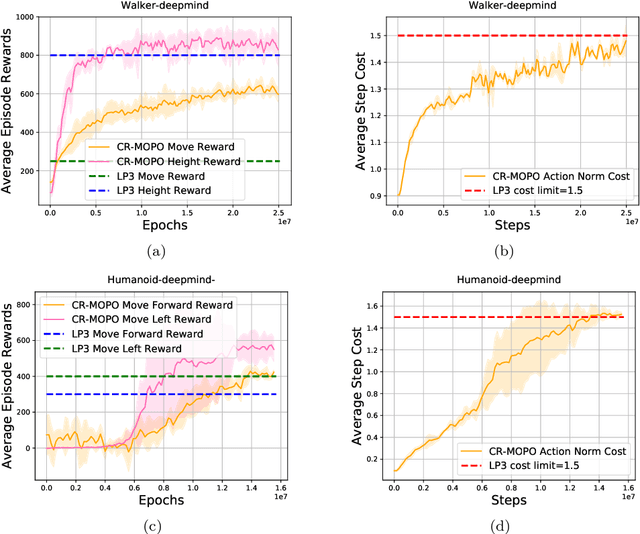
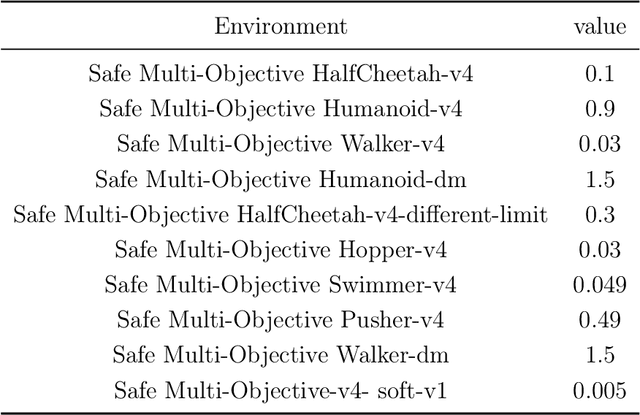
In numerous reinforcement learning (RL) problems involving safety-critical systems, a key challenge lies in balancing multiple objectives while simultaneously meeting all stringent safety constraints. To tackle this issue, we propose a primal-based framework that orchestrates policy optimization between multi-objective learning and constraint adherence. Our method employs a novel natural policy gradient manipulation method to optimize multiple RL objectives and overcome conflicting gradients between different tasks, since the simple weighted average gradient direction may not be beneficial for specific tasks' performance due to misaligned gradients of different task objectives. When there is a violation of a hard constraint, our algorithm steps in to rectify the policy to minimize this violation. We establish theoretical convergence and constraint violation guarantees in a tabular setting. Empirically, our proposed method also outperforms prior state-of-the-art methods on challenging safe multi-objective reinforcement learning tasks.

A CMDP-within-online framework for Meta-Safe Reinforcement Learning

Meta-reinforcement learning has widely been used as a learning-to-learn framework to solve unseen tasks with limited experience. However, the aspect of constraint violations has not been adequately addressed in the existing works, making their application restricted in real-world settings. In this paper, we study the problem of meta-safe reinforcement learning (Meta-SRL) through the CMDP-within-online framework to establish the first provable guarantees in this important setting. We obtain task-averaged regret bounds for the reward maximization (optimality gap) and constraint violations using gradient-based meta-learning and show that the task-averaged optimality gap and constraint satisfaction improve with task-similarity in a static environment or task-relatedness in a dynamic environment. Several technical challenges arise when making this framework practical. To this end, we propose a meta-algorithm that performs inexact online learning on the upper bounds of within-task optimality gap and constraint violations estimated by off-policy stationary distribution corrections. Furthermore, we enable the learning rates to be adapted for every task and extend our approach to settings with a competing dynamically changing oracle. Finally, experiments are conducted to demonstrate the effectiveness of our approach.

Balance Reward and Safety Optimization for Safe Reinforcement Learning: A Perspective of Gradient Manipulation

Ensuring the safety of Reinforcement Learning (RL) is crucial for its deployment in real-world applications. Nevertheless, managing the trade-off between reward and safety during exploration presents a significant challenge. Improving reward performance through policy adjustments may adversely affect safety performance. In this study, we aim to address this conflicting relation by leveraging the theory of gradient manipulation. Initially, we analyze the conflict between reward and safety gradients. Subsequently, we tackle the balance between reward and safety optimization by proposing a soft switching policy optimization method, for which we provide convergence analysis. Based on our theoretical examination, we provide a safe RL framework to overcome the aforementioned challenge, and we develop a Safety-MuJoCo Benchmark to assess the performance of safe RL algorithms. Finally, we evaluate the effectiveness of our method on the Safety-MuJoCo Benchmark and a popular safe benchmark, Omnisafe. Experimental results demonstrate that our algorithms outperform several state-of-the-art baselines in terms of balancing reward and safety optimization.

Tempo Adaption in Non-stationary Reinforcement Learning

We first raise and tackle ``time synchronization'' issue between the agent and the environment in non-stationary reinforcement learning (RL), a crucial factor hindering its real-world applications. In reality, environmental changes occur over wall-clock time ($\mathfrak{t}$) rather than episode progress ($k$), where wall-clock time signifies the actual elapsed time within the fixed duration $\mathfrak{t} \in [0, T]$. In existing works, at episode $k$, the agent rollouts a trajectory and trains a policy before transitioning to episode $k+1$. In the context of the time-desynchronized environment, however, the agent at time $\mathfrak{t}_k$ allocates $\Delta \mathfrak{t}$ for trajectory generation and training, subsequently moves to the next episode at $\mathfrak{t}_{k+1}=\mathfrak{t}_{k}+\Delta \mathfrak{t}$. Despite a fixed total episode ($K$), the agent accumulates different trajectories influenced by the choice of \textit{interaction times} ($\mathfrak{t}_1,\mathfrak{t}_2,...,\mathfrak{t}_K$), significantly impacting the sub-optimality gap of policy. We propose a Proactively Synchronizing Tempo (ProST) framework that computes optimal $\{ \mathfrak{t}_1,\mathfrak{t}_2,...,\mathfrak{t}_K \} (= \{ \mathfrak{t} \}_{1:K})$. Our main contribution is that we show optimal $\{ \mathfrak{t} \}_{1:K}$ trades-off between the policy training time (agent tempo) and how fast the environment changes (environment tempo). Theoretically, this work establishes an optimal $\{ \mathfrak{t} \}_{1:K}$ as a function of the degree of the environment's non-stationarity while also achieving a sublinear dynamic regret. Our experimental evaluation on various high dimensional non-stationary environments shows that the ProST framework achieves a higher online return at optimal $\{ \mathfrak{t} \}_{1:K}$ than the existing methods.

Scalable Primal-Dual Actor-Critic Method for Safe Multi-Agent RL with General Utilities

We investigate safe multi-agent reinforcement learning, where agents seek to collectively maximize an aggregate sum of local objectives while satisfying their own safety constraints. The objective and constraints are described by {\it general utilities}, i.e., nonlinear functions of the long-term state-action occupancy measure, which encompass broader decision-making goals such as risk, exploration, or imitations. The exponential growth of the state-action space size with the number of agents presents challenges for global observability, further exacerbated by the global coupling arising from agents' safety constraints. To tackle this issue, we propose a primal-dual method utilizing shadow reward and $\kappa$-hop neighbor truncation under a form of correlation decay property, where $\kappa$ is the communication radius. In the exact setting, our algorithm converges to a first-order stationary point (FOSP) at the rate of $\mathcal{O}\left(T^{-2/3}\right)$. In the sample-based setting, we demonstrate that, with high probability, our algorithm requires $\widetilde{\mathcal{O}}\left(\epsilon^{-3.5}\right)$ samples to achieve an $\epsilon$-FOSP with an approximation error of $\mathcal{O}(\phi_0^{2\kappa})$, where $\phi_0\in (0,1)$. Finally, we demonstrate the effectiveness of our model through extensive numerical experiments.

DyBit: Dynamic Bit-Precision Numbers for Efficient Quantized Neural Network Inference

To accelerate the inference of deep neural networks (DNNs), quantization with low-bitwidth numbers is actively researched. A prominent challenge is to quantize the DNN models into low-bitwidth numbers without significant accuracy degradation, especially at very low bitwidths (< 8 bits). This work targets an adaptive data representation with variable-length encoding called DyBit. DyBit can dynamically adjust the precision and range of separate bit-field to be adapted to the DNN weights/activations distribution. We also propose a hardware-aware quantization framework with a mixed-precision accelerator to trade-off the inference accuracy and speedup. Experimental results demonstrate that the inference accuracy via DyBit is 1.997% higher than the state-of-the-art at 4-bit quantization, and the proposed framework can achieve up to 8.1x speedup compared with the original model.

Scalable Multi-Agent Reinforcement Learning with General Utilities

We study the scalable multi-agent reinforcement learning (MARL) with general utilities, defined as nonlinear functions of the team's long-term state-action occupancy measure. The objective is to find a localized policy that maximizes the average of the team's local utility functions without the full observability of each agent in the team. By exploiting the spatial correlation decay property of the network structure, we propose a scalable distributed policy gradient algorithm with shadow reward and localized policy that consists of three steps: (1) shadow reward estimation, (2) truncated shadow Q-function estimation, and (3) truncated policy gradient estimation and policy update. Our algorithm converges, with high probability, to $\epsilon$-stationarity with $\widetilde{\mc{O}}(\epsilon^{-2})$ samples up to some approximation error that decreases exponentially in the communication radius. This is the first result in the literature on multi-agent RL with general utilities that does not require the full observability.

Non-stationary Risk-sensitive Reinforcement Learning: Near-optimal Dynamic Regret, Adaptive Detection, and Separation Design

We study risk-sensitive reinforcement learning (RL) based on an entropic risk measure in episodic non-stationary Markov decision processes (MDPs). Both the reward functions and the state transition kernels are unknown and allowed to vary arbitrarily over time with a budget on their cumulative variations. When this variation budget is known a prior, we propose two restart-based algorithms, namely Restart-RSMB and Restart-RSQ, and establish their dynamic regrets. Based on these results, we further present a meta-algorithm that does not require any prior knowledge of the variation budget and can adaptively detect the non-stationarity on the exponential value functions. A dynamic regret lower bound is then established for non-stationary risk-sensitive RL to certify the near-optimality of the proposed algorithms. Our results also show that the risk control and the handling of the non-stationarity can be separately designed in the algorithm if the variation budget is known a prior, while the non-stationary detection mechanism in the adaptive algorithm depends on the risk parameter. This work offers the first non-asymptotic theoretical analyses for the non-stationary risk-sensitive RL in the literature.

Policy-based Primal-Dual Methods for Convex Constrained Markov Decision Processes

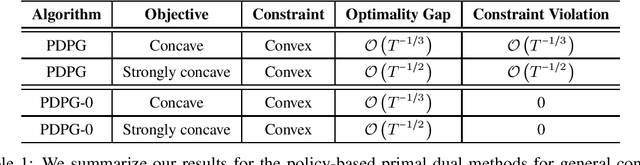
We study convex Constrained Markov Decision Processes (CMDPs) in which the objective is concave and the constraints are convex in the state-action visitation distribution. We propose a policy-based primal-dual algorithm that updates the primal variable via policy gradient ascent and updates the dual variable via projected sub-gradient descent. Despite the loss of additivity structure and the nonconvex nature, we establish the global convergence of the proposed algorithm by leveraging a hidden convexity in the problem under the general soft-max parameterization, and prove the $\mathcal{O}\left(T^{-1/3}\right)$ convergence rate in terms of both optimality gap and constraint violation. When the objective is strongly concave in the visitation distribution, we prove an improved convergence rate of $\mathcal{O}\left(T^{-1/2}\right)$. By introducing a pessimistic term to the constraint, we further show that a zero constraint violation can be achieved while preserving the same convergence rate for the optimality gap. This work is the first one in the literature that establishes non-asymptotic convergence guarantees for policy-based primal-dual methods for solving infinite-horizon discounted convex CMDPs.