Policy-based Primal-Dual Methods for Convex Constrained Markov Decision Processes
Paper and Code
May 22, 2022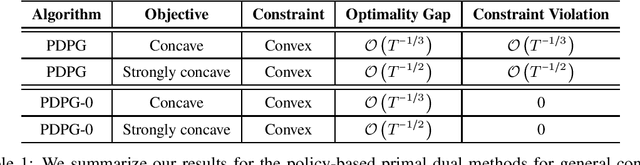
We study convex Constrained Markov Decision Processes (CMDPs) in which the objective is concave and the constraints are convex in the state-action visitation distribution. We propose a policy-based primal-dual algorithm that updates the primal variable via policy gradient ascent and updates the dual variable via projected sub-gradient descent. Despite the loss of additivity structure and the nonconvex nature, we establish the global convergence of the proposed algorithm by leveraging a hidden convexity in the problem under the general soft-max parameterization, and prove the $\mathcal{O}\left(T^{-1/3}\right)$ convergence rate in terms of both optimality gap and constraint violation. When the objective is strongly concave in the visitation distribution, we prove an improved convergence rate of $\mathcal{O}\left(T^{-1/2}\right)$. By introducing a pessimistic term to the constraint, we further show that a zero constraint violation can be achieved while preserving the same convergence rate for the optimality gap. This work is the first one in the literature that establishes non-asymptotic convergence guarantees for policy-based primal-dual methods for solving infinite-horizon discounted convex CMDPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge