Policy-based Primal-Dual Methods for Convex Constrained Markov Decision Processes

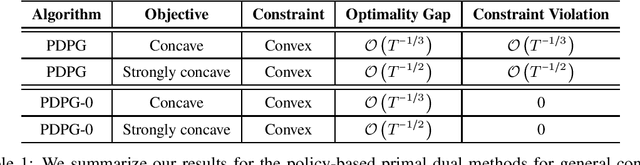
We study convex Constrained Markov Decision Processes (CMDPs) in which the objective is concave and the constraints are convex in the state-action visitation distribution. We propose a policy-based primal-dual algorithm that updates the primal variable via policy gradient ascent and updates the dual variable via projected sub-gradient descent. Despite the loss of additivity structure and the nonconvex nature, we establish the global convergence of the proposed algorithm by leveraging a hidden convexity in the problem under the general soft-max parameterization, and prove the $\mathcal{O}\left(T^{-1/3}\right)$ convergence rate in terms of both optimality gap and constraint violation. When the objective is strongly concave in the visitation distribution, we prove an improved convergence rate of $\mathcal{O}\left(T^{-1/2}\right)$. By introducing a pessimistic term to the constraint, we further show that a zero constraint violation can be achieved while preserving the same convergence rate for the optimality gap. This work is the first one in the literature that establishes non-asymptotic convergence guarantees for policy-based primal-dual methods for solving infinite-horizon discounted convex CMDPs.

Integrated Conditional Estimation-Optimization

Many real-world optimization problems involve uncertain parameters with probability distributions that can be estimated using contextual feature information. In contrast to the standard approach of first estimating the distribution of uncertain parameters and then optimizing the objective based on the estimation, we propose an integrated conditional estimation-optimization (ICEO) framework that estimates the underlying conditional distribution of the random parameter while considering the structure of the optimization problem. We directly model the relationship between the conditional distribution of the random parameter and the contextual features, and then estimate the probabilistic model with an objective that aligns with the downstream optimization problem. We show that our ICEO approach is asymptotically consistent under moderate regularity conditions and further provide finite performance guarantees in the form of generalization bounds. Computationally, performing estimation with the ICEO approach is a non-convex and often non-differentiable optimization problem. We propose a general methodology for approximating the potentially non-differentiable mapping from estimated conditional distribution to the optimal decision by a differentiable function, which greatly improves the performance of gradient-based algorithms applied to the non-convex problem. We also provide a polynomial optimization solution approach in the semi-algebraic case. Numerical experiments are also conducted to show the empirical success of our approach in different situations including with limited data samples and model mismatches.

Fatigue-aware Bandits for Dependent Click Models

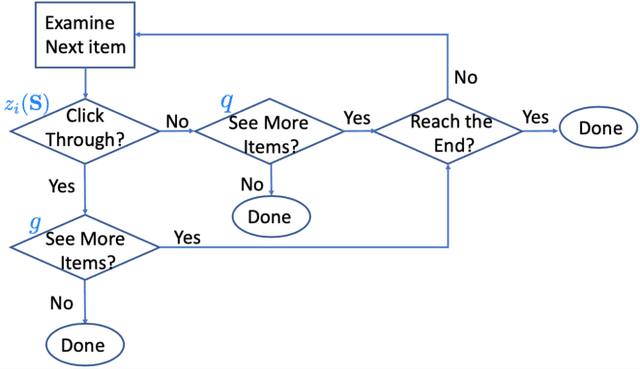
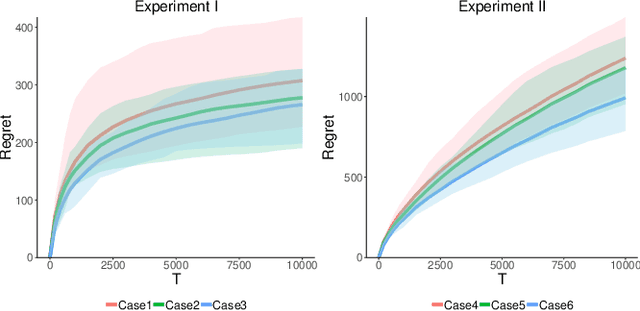
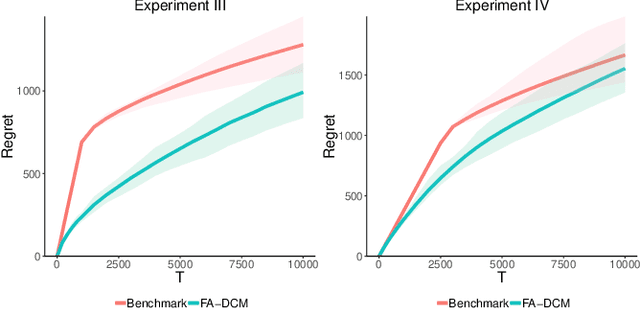
As recommender systems send a massive amount of content to keep users engaged, users may experience fatigue which is contributed by 1) an overexposure to irrelevant content, 2) boredom from seeing too many similar recommendations. To address this problem, we consider an online learning setting where a platform learns a policy to recommend content that takes user fatigue into account. We propose an extension of the Dependent Click Model (DCM) to describe users' behavior. We stipulate that for each piece of content, its attractiveness to a user depends on its intrinsic relevance and a discount factor which measures how many similar contents have been shown. Users view the recommended content sequentially and click on the ones that they find attractive. Users may leave the platform at any time, and the probability of exiting is higher when they do not like the content. Based on user's feedback, the platform learns the relevance of the underlying content as well as the discounting effect due to content fatigue. We refer to this learning task as "fatigue-aware DCM Bandit" problem. We consider two learning scenarios depending on whether the discounting effect is known. For each scenario, we propose a learning algorithm which simultaneously explores and exploits, and characterize its regret bound.