Beyond Discretization: Learning the Optimal Solution Path

Many applications require minimizing a family of optimization problems indexed by some hyperparameter $\lambda \in \Lambda$ to obtain an entire solution path. Traditional approaches proceed by discretizing $\Lambda$ and solving a series of optimization problems. We propose an alternative approach that parameterizes the solution path with a set of basis functions and solves a \emph{single} stochastic optimization problem to learn the entire solution path. Our method offers substantial complexity improvements over discretization. When using constant-step size SGD, the uniform error of our learned solution path relative to the true path exhibits linear convergence to a constant related to the expressiveness of the basis. When the true solution path lies in the span of the basis, this constant is zero. We also prove stronger results for special cases common in machine learning: When $\lambda \in [-1, 1]$ and the solution path is $\nu$-times differentiable, constant step-size SGD learns a path with $\epsilon$ uniform error after at most $O(\epsilon^{\frac{1}{1-\nu}} \log(1/\epsilon))$ iterations, and when the solution path is analytic, it only requires $O\left(\log^2(1/\epsilon)\log\log(1/\epsilon)\right)$. By comparison, the best-known discretization schemes in these settings require at least $O(\epsilon^{-1/2})$ discretization points (and even more gradient calls). Finally, we propose an adaptive variant of our method that sequentially adds basis functions and demonstrates strong numerical performance through experiments.

Binary Classification with Instance and Label Dependent Label Noise

Learning with label dependent label noise has been extensively explored in both theory and practice; however, dealing with instance (i.e., feature) and label dependent label noise continues to be a challenging task. The difficulty arises from the fact that the noise rate varies for each instance, making it challenging to estimate accurately. The question of whether it is possible to learn a reliable model using only noisy samples remains unresolved. We answer this question with a theoretical analysis that provides matching upper and lower bounds. Surprisingly, our results show that, without any additional assumptions, empirical risk minimization achieves the optimal excess risk bound. Specifically, we derive a novel excess risk bound proportional to the noise level, which holds in very general settings, by comparing the empirical risk minimizers obtained from clean samples and noisy samples. Second, we show that the minimax lower bound for the 0-1 loss is a constant proportional to the average noise rate. Our findings suggest that learning solely with noisy samples is impossible without access to clean samples or strong assumptions on the distribution of the data.

Active Learning in the Predict-then-Optimize Framework: A Margin-Based Approach

We develop the first active learning method in the predict-then-optimize framework. Specifically, we develop a learning method that sequentially decides whether to request the "labels" of feature samples from an unlabeled data stream, where the labels correspond to the parameters of an optimization model for decision-making. Our active learning method is the first to be directly informed by the decision error induced by the predicted parameters, which is referred to as the Smart Predict-then-Optimize (SPO) loss. Motivated by the structure of the SPO loss, our algorithm adopts a margin-based criterion utilizing the concept of distance to degeneracy and minimizes a tractable surrogate of the SPO loss on the collected data. In particular, we develop an efficient active learning algorithm with both hard and soft rejection variants, each with theoretical excess risk (i.e., generalization) guarantees. We further derive bounds on the label complexity, which refers to the number of samples whose labels are acquired to achieve a desired small level of SPO risk. Under some natural low-noise conditions, we show that these bounds can be better than the naive supervised learning approach that labels all samples. Furthermore, when using the SPO+ loss function, a specialized surrogate of the SPO loss, we derive a significantly smaller label complexity under separability conditions. We also present numerical evidence showing the practical value of our proposed algorithms in the settings of personalized pricing and the shortest path problem.

Online Contextual Decision-Making with a Smart Predict-then-Optimize Method

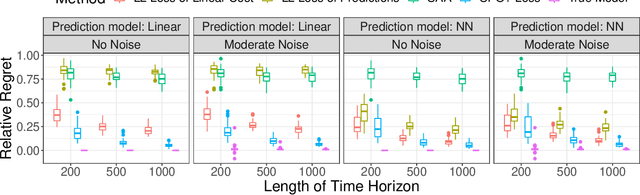
We study an online contextual decision-making problem with resource constraints. At each time period, the decision-maker first predicts a reward vector and resource consumption matrix based on a given context vector and then solves a downstream optimization problem to make a decision. The final goal of the decision-maker is to maximize the summation of the reward and the utility from resource consumption, while satisfying the resource constraints. We propose an algorithm that mixes a prediction step based on the "Smart Predict-then-Optimize (SPO)" method with a dual update step based on mirror descent. We prove regret bounds and demonstrate that the overall convergence rate of our method depends on the $\mathcal{O}(T^{-1/2})$ convergence of online mirror descent as well as risk bounds of the surrogate loss function used to learn the prediction model. Our algorithm and regret bounds apply to a general convex feasible region for the resource constraints, including both hard and soft resource constraint cases, and they apply to a wide class of prediction models in contrast to the traditional settings of linear contextual models or finite policy spaces. We also conduct numerical experiments to empirically demonstrate the strength of our proposed SPO-type methods, as compared to traditional prediction-error-only methods, on multi-dimensional knapsack and longest path instances.

Integrated Conditional Estimation-Optimization

Many real-world optimization problems involve uncertain parameters with probability distributions that can be estimated using contextual feature information. In contrast to the standard approach of first estimating the distribution of uncertain parameters and then optimizing the objective based on the estimation, we propose an integrated conditional estimation-optimization (ICEO) framework that estimates the underlying conditional distribution of the random parameter while considering the structure of the optimization problem. We directly model the relationship between the conditional distribution of the random parameter and the contextual features, and then estimate the probabilistic model with an objective that aligns with the downstream optimization problem. We show that our ICEO approach is asymptotically consistent under moderate regularity conditions and further provide finite performance guarantees in the form of generalization bounds. Computationally, performing estimation with the ICEO approach is a non-convex and often non-differentiable optimization problem. We propose a general methodology for approximating the potentially non-differentiable mapping from estimated conditional distribution to the optimal decision by a differentiable function, which greatly improves the performance of gradient-based algorithms applied to the non-convex problem. We also provide a polynomial optimization solution approach in the semi-algebraic case. Numerical experiments are also conducted to show the empirical success of our approach in different situations including with limited data samples and model mismatches.

Risk Bounds and Calibration for a Smart Predict-then-Optimize Method

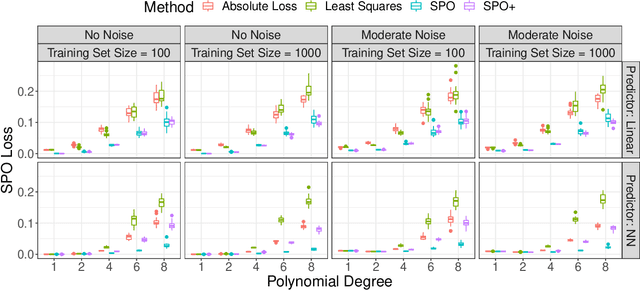
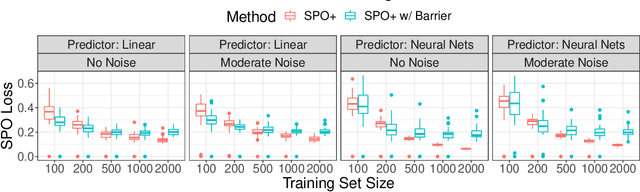
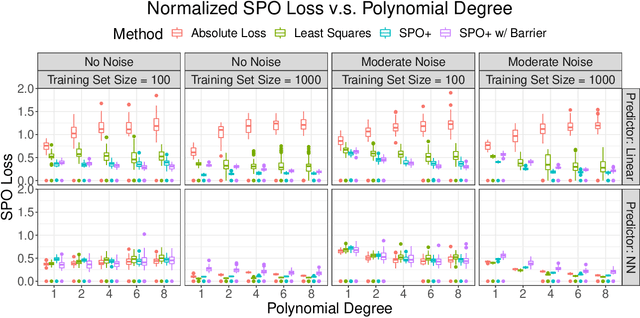
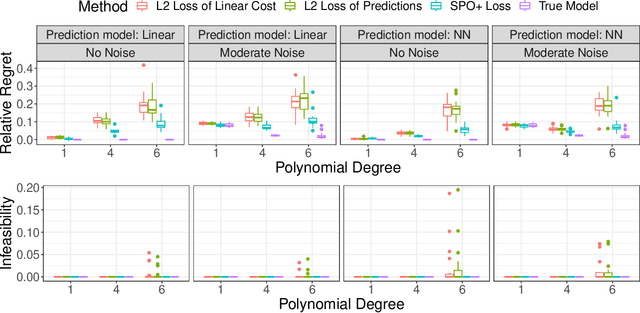
The predict-then-optimize framework is fundamental in practical stochastic decision-making problems: first predict unknown parameters of an optimization model, then solve the problem using the predicted values. A natural loss function in this setting is defined by measuring the decision error induced by the predicted parameters, which was named the Smart Predict-then-Optimize (SPO) loss by Elmachtoub and Grigas [arXiv:1710.08005]. Since the SPO loss is typically nonconvex and possibly discontinuous, Elmachtoub and Grigas [arXiv:1710.08005] introduced a convex surrogate, called the SPO+ loss, that importantly accounts for the underlying structure of the optimization model. In this paper, we greatly expand upon the consistency results for the SPO+ loss provided by Elmachtoub and Grigas [arXiv:1710.08005]. We develop risk bounds and uniform calibration results for the SPO+ loss relative to the SPO loss, which provide a quantitative way to transfer the excess surrogate risk to excess true risk. By combining our risk bounds with generalization bounds, we show that the empirical minimizer of the SPO+ loss achieves low excess true risk with high probability. We first demonstrate these results in the case when the feasible region of the underlying optimization problem is a polyhedron, and then we show that the results can be strengthened substantially when the feasible region is a level set of a strongly convex function. We perform experiments to empirically demonstrate the strength of the SPO+ surrogate, as compared to standard $\ell_1$ and squared $\ell_2$ prediction error losses, on portfolio allocation and cost-sensitive multi-class classification problems.

Joint Online Learning and Decision-making via Dual Mirror Descent

We consider an online revenue maximization problem over a finite time horizon subject to lower and upper bounds on cost. At each period, an agent receives a context vector sampled i.i.d. from an unknown distribution and needs to make a decision adaptively. The revenue and cost functions depend on the context vector as well as some fixed but possibly unknown parameter vector to be learned. We propose a novel offline benchmark and a new algorithm that mixes an online dual mirror descent scheme with a generic parameter learning process. When the parameter vector is known, we demonstrate an $O(\sqrt{T})$ regret result as well an $O(\sqrt{T})$ bound on the possible constraint violations. When the parameter is not known and must be learned, we demonstrate that the regret and constraint violations are the sums of the previous $O(\sqrt{T})$ terms plus terms that directly depend on the convergence of the learning process.

Stochastic In-Face Frank-Wolfe Methods for Non-Convex Optimization and Sparse Neural Network Training

The Frank-Wolfe method and its extensions are well-suited for delivering solutions with desirable structural properties, such as sparsity or low-rank structure. We introduce a new variant of the Frank-Wolfe method that combines Frank-Wolfe steps and steepest descent steps, as well as a novel modification of the "Frank-Wolfe gap" to measure convergence in the non-convex case. We further extend this method to incorporate in-face directions for preserving structured solutions as well as block coordinate steps, and we demonstrate computational guarantees in terms of the modified Frank-Wolfe gap for all of these variants. We are particularly motivated by the application of this methodology to the training of neural networks with sparse properties, and we apply our block coordinate method to the problem of $\ell_1$ regularized neural network training. We present the results of several numerical experiments on both artificial and real datasets demonstrating significant improvements of our method in training sparse neural networks.

Generalization Bounds in the Predict-then-Optimize Framework

The predict-then-optimize framework is fundamental in many practical settings: predict the unknown parameters of an optimization problem, and then solve the problem using the predicted values of the parameters. A natural loss function in this environment is to consider the cost of the decisions induced by the predicted parameters, in contrast to the prediction error of the parameters. This loss function was recently introduced in Elmachtoub and Grigas (2017), which called it the Smart Predict-then-Optimize (SPO) loss. Since the SPO loss is nonconvex and noncontinuous, standard results for deriving generalization bounds do not apply. In this work, we provide an assortment of generalization bounds for the SPO loss function. In particular, we derive bounds based on the Natarajan dimension that, in the case of a polyhedral feasible region, scale at most logarithmically in the number of extreme points, but, in the case of a general convex set, have poor dependence on the dimension. By exploiting the structure of the SPO loss function and an additional strong convexity assumption on the feasible region, we can dramatically improve the dependence on the dimension via an analysis and corresponding bounds that are akin to the margin guarantees in classification problems.

Condition Number Analysis of Logistic Regression, and its Implications for Standard First-Order Solution Methods

Logistic regression is one of the most popular methods in binary classification, wherein estimation of model parameters is carried out by solving the maximum likelihood (ML) optimization problem, and the ML estimator is defined to be the optimal solution of this problem. It is well known that the ML estimator exists when the data is non-separable, but fails to exist when the data is separable. First-order methods are the algorithms of choice for solving large-scale instances of the logistic regression problem. In this paper, we introduce a pair of condition numbers that measure the degree of non-separability or separability of a given dataset in the setting of binary classification, and we study how these condition numbers relate to and inform the properties and the convergence guarantees of first-order methods. When the training data is non-separable, we show that the degree of non-separability naturally enters the analysis and informs the properties and convergence guarantees of two standard first-order methods: steepest descent (for any given norm) and stochastic gradient descent. Expanding on the work of Bach, we also show how the degree of non-separability enters into the analysis of linear convergence of steepest descent (without needing strong convexity), as well as the adaptive convergence of stochastic gradient descent. When the training data is separable, first-order methods rather curiously have good empirical success, which is not well understood in theory. In the case of separable data, we demonstrate how the degree of separability enters into the analysis of $\ell_2$ steepest descent and stochastic gradient descent for delivering approximate-maximum-margin solutions with associated computational guarantees as well. This suggests that first-order methods can lead to statistically meaningful solutions in the separable case, even though the ML solution does not exist.