On the Practice of Deep Hierarchical Ensemble Network for Ad Conversion Rate Prediction

The predictions of click through rate (CTR) and conversion rate (CVR) play a crucial role in the success of ad-recommendation systems. A Deep Hierarchical Ensemble Network (DHEN) has been proposed to integrate multiple feature crossing modules and has achieved great success in CTR prediction. However, its performance for CVR prediction is unclear in the conversion ads setting, where an ad bids for the probability of a user's off-site actions on a third party website or app, including purchase, add to cart, sign up, etc. A few challenges in DHEN: 1) What feature-crossing modules (MLP, DCN, Transformer, to name a few) should be included in DHEN? 2) How deep and wide should DHEN be to achieve the best trade-off between efficiency and efficacy? 3) What hyper-parameters to choose in each feature-crossing module? Orthogonal to the model architecture, the input personalization features also significantly impact model performance with a high degree of freedom. In this paper, we attack this problem and present our contributions biased to the applied data science side, including: First, we propose a multitask learning framework with DHEN as the single backbone model architecture to predict all CVR tasks, with a detailed study on how to make DHEN work effectively in practice; Second, we build both on-site real-time user behavior sequences and off-site conversion event sequences for CVR prediction purposes, and conduct ablation study on its importance; Last but not least, we propose a self-supervised auxiliary loss to predict future actions in the input sequence, to help resolve the label sparseness issue in CVR prediction. Our method achieves state-of-the-art performance compared to previous single feature crossing modules with pre-trained user personalization features.

Online MDP with Transition Prototypes: A Robust Adaptive Approach

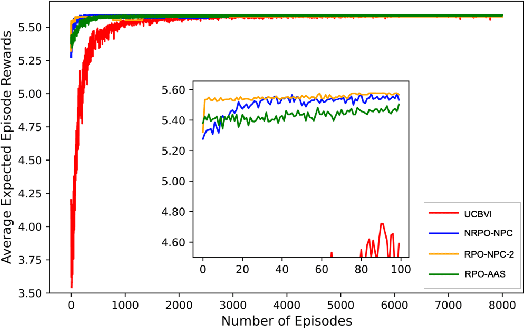
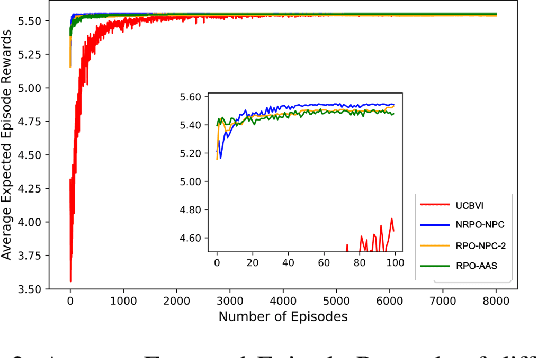
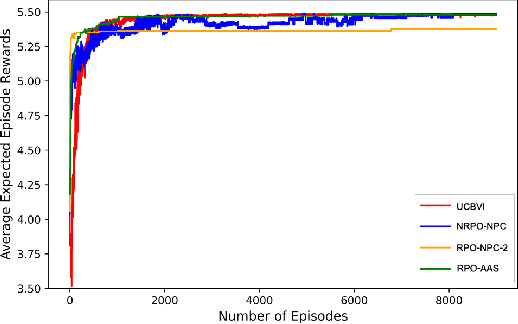
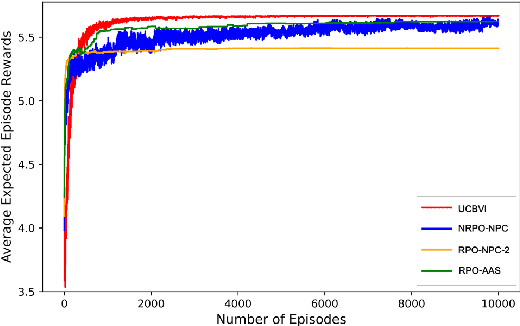
In this work, we consider an online robust Markov Decision Process (MDP) where we have the information of finitely many prototypes of the underlying transition kernel. We consider an adaptively updated ambiguity set of the prototypes and propose an algorithm that efficiently identifies the true underlying transition kernel while guaranteeing the performance of the corresponding robust policy. To be more specific, we provide a sublinear regret of the subsequent optimal robust policy. We also provide an early stopping mechanism and a worst-case performance bound of the value function. In numerical experiments, we demonstrate that our method outperforms existing approaches, particularly in the early stage with limited data. This work contributes to robust MDPs by considering possible prior information about the underlying transition probability and online learning, offering both theoretical insights and practical algorithms for improved decision-making under uncertainty.

Integrated Conditional Estimation-Optimization

Many real-world optimization problems involve uncertain parameters with probability distributions that can be estimated using contextual feature information. In contrast to the standard approach of first estimating the distribution of uncertain parameters and then optimizing the objective based on the estimation, we propose an integrated conditional estimation-optimization (ICEO) framework that estimates the underlying conditional distribution of the random parameter while considering the structure of the optimization problem. We directly model the relationship between the conditional distribution of the random parameter and the contextual features, and then estimate the probabilistic model with an objective that aligns with the downstream optimization problem. We show that our ICEO approach is asymptotically consistent under moderate regularity conditions and further provide finite performance guarantees in the form of generalization bounds. Computationally, performing estimation with the ICEO approach is a non-convex and often non-differentiable optimization problem. We propose a general methodology for approximating the potentially non-differentiable mapping from estimated conditional distribution to the optimal decision by a differentiable function, which greatly improves the performance of gradient-based algorithms applied to the non-convex problem. We also provide a polynomial optimization solution approach in the semi-algebraic case. Numerical experiments are also conducted to show the empirical success of our approach in different situations including with limited data samples and model mismatches.

Smart Feasibility Pump: Reinforcement Learning for (Mixed) Integer Programming

In this work, we propose a deep reinforcement learning (DRL) model for finding a feasible solution for (mixed) integer programming (MIP) problems. Finding a feasible solution for MIP problems is critical because many successful heuristics rely on a known initial feasible solution. However, it is in general NP-hard. Inspired by the feasibility pump (FP), a well-known heuristic for searching feasible MIP solutions, we develop a smart feasibility pump (SFP) method using DRL. In addition to multi-layer perception (MLP), we propose a novel convolution neural network (CNN) structure for the policy network to capture the hidden information of the constraint matrix of the MIP problem. Numerical experiments on various problem instances show that SFP significantly outperforms the classic FP in terms of the number of steps required to reach the first feasible solution. Moreover, the CNN structure works without the projection of the current solution as the input, which saves the computational effort at each step of the FP algorithms to find projections. This highlights the representational power of the CNN structure.