Online MDP with Transition Prototypes: A Robust Adaptive Approach
Paper and Code
Dec 19, 2024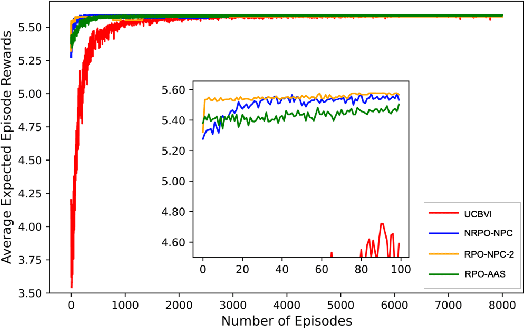
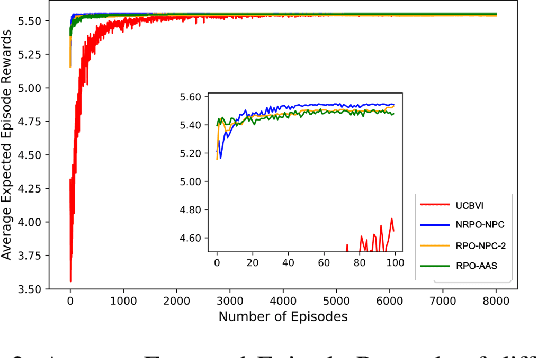
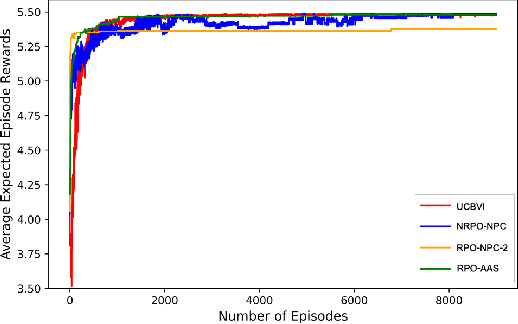
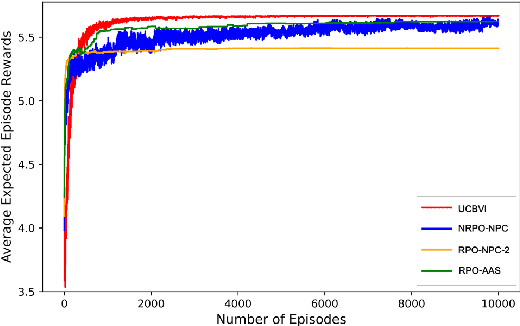
In this work, we consider an online robust Markov Decision Process (MDP) where we have the information of finitely many prototypes of the underlying transition kernel. We consider an adaptively updated ambiguity set of the prototypes and propose an algorithm that efficiently identifies the true underlying transition kernel while guaranteeing the performance of the corresponding robust policy. To be more specific, we provide a sublinear regret of the subsequent optimal robust policy. We also provide an early stopping mechanism and a worst-case performance bound of the value function. In numerical experiments, we demonstrate that our method outperforms existing approaches, particularly in the early stage with limited data. This work contributes to robust MDPs by considering possible prior information about the underlying transition probability and online learning, offering both theoretical insights and practical algorithms for improved decision-making under uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge