Self-Supervised Penalty-Based Learning for Robust Constrained Optimization

We propose a new methodology for parameterized constrained robust optimization, an important class of optimization problems under uncertainty, based on learning with a self-supervised penalty-based loss function. Whereas supervised learning requires pre-solved instances for training, our approach leverages a custom loss function derived from the exact penalty method in optimization to learn an approximation, typically defined by a neural network model, of the parameterized optimal solution mapping. Additionally, we adapt our approach to robust constrained combinatorial optimization problems by incorporating a surrogate linear cost over mixed integer domains, and a smooth approximations thereof, into the final layer of the network architecture. We perform computational experiments to test our approach on three different applications: multidimensional knapsack with continuous variables, combinatorial multidimensional knapsack with discrete variables, and an inventory management problem. Our results demonstrate that our self-supervised approach is able to effectively learn neural network approximations whose inference time is significantly smaller than the computation time of traditional solvers for this class of robust optimization problems. Furthermore, our results demonstrate that by varying the penalty parameter we are able to effectively balance the trade-off between sub-optimality and robust feasibility of the obtained solutions.

Monte Carlo Augmented Actor-Critic for Sparse Reward Deep Reinforcement Learning from Suboptimal Demonstrations

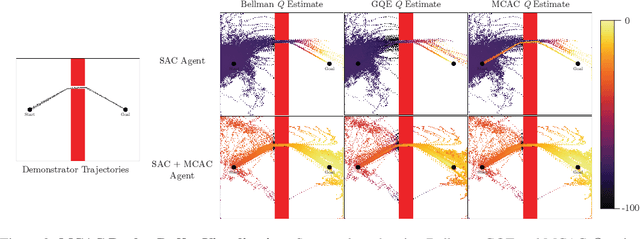
Providing densely shaped reward functions for RL algorithms is often exceedingly challenging, motivating the development of RL algorithms that can learn from easier-to-specify sparse reward functions. This sparsity poses new exploration challenges. One common way to address this problem is using demonstrations to provide initial signal about regions of the state space with high rewards. However, prior RL from demonstrations algorithms introduce significant complexity and many hyperparameters, making them hard to implement and tune. We introduce Monte Carlo Augmented Actor Critic (MCAC), a parameter free modification to standard actor-critic algorithms which initializes the replay buffer with demonstrations and computes a modified $Q$-value by taking the maximum of the standard temporal distance (TD) target and a Monte Carlo estimate of the reward-to-go. This encourages exploration in the neighborhood of high-performing trajectories by encouraging high $Q$-values in corresponding regions of the state space. Experiments across $5$ continuous control domains suggest that MCAC can be used to significantly increase learning efficiency across $6$ commonly used RL and RL-from-demonstrations algorithms. See https://sites.google.com/view/mcac-rl for code and supplementary material.