Absence of spurious solutions far from ground truth: A low-rank analysis with high-order losses

Matrix sensing problems exhibit pervasive non-convexity, plaguing optimization with a proliferation of suboptimal spurious solutions. Avoiding convergence to these critical points poses a major challenge. This work provides new theoretical insights that help demystify the intricacies of the non-convex landscape. In this work, we prove that under certain conditions, critical points sufficiently distant from the ground truth matrix exhibit favorable geometry by being strict saddle points rather than troublesome local minima. Moreover, we introduce the notion of higher-order losses for the matrix sensing problem and show that the incorporation of such losses into the objective function amplifies the negative curvature around those distant critical points. This implies that increasing the complexity of the objective function via high-order losses accelerates the escape from such critical points and acts as a desirable alternative to increasing the complexity of the optimization problem via over-parametrization. By elucidating key characteristics of the non-convex optimization landscape, this work makes progress towards a comprehensive framework for tackling broader machine learning objectives plagued by non-convexity.

Algorithmic Regularization in Tensor Optimization: Towards a Lifted Approach in Matrix Sensing

Gradient descent (GD) is crucial for generalization in machine learning models, as it induces implicit regularization, promoting compact representations. In this work, we examine the role of GD in inducing implicit regularization for tensor optimization, particularly within the context of the lifted matrix sensing framework. This framework has been recently proposed to address the non-convex matrix sensing problem by transforming spurious solutions into strict saddles when optimizing over symmetric, rank-1 tensors. We show that, with sufficiently small initialization scale, GD applied to this lifted problem results in approximate rank-1 tensors and critical points with escape directions. Our findings underscore the significance of the tensor parametrization of matrix sensing, in combination with first-order methods, in achieving global optimality in such problems.

Over-parametrization via Lifting for Low-rank Matrix Sensing: Conversion of Spurious Solutions to Strict Saddle Points

This paper studies the role of over-parametrization in solving non-convex optimization problems. The focus is on the important class of low-rank matrix sensing, where we propose an infinite hierarchy of non-convex problems via the lifting technique and the Burer-Monteiro factorization. This contrasts with the existing over-parametrization technique where the search rank is limited by the dimension of the matrix and it does not allow a rich over-parametrization of an arbitrary degree. We show that although the spurious solutions of the problem remain stationary points through the hierarchy, they will be transformed into strict saddle points (under some technical conditions) and can be escaped via local search methods. This is the first result in the literature showing that over-parametrization creates a negative curvature for escaping spurious solutions. We also derive a bound on how much over-parametrization is requited to enable the elimination of spurious solutions.

Semidefinite Programming versus Burer-Monteiro Factorization for Matrix Sensing

Many fundamental low-rank optimization problems, such as matrix completion, phase synchronization/retrieval, power system state estimation, and robust PCA, can be formulated as the matrix sensing problem. Two main approaches for solving matrix sensing are based on semidefinite programming (SDP) and Burer-Monteiro (B-M) factorization. The SDP method suffers from high computational and space complexities, whereas the B-M method may return a spurious solution due to the non-convexity of the problem. The existing theoretical guarantees for the success of these methods have led to similar conservative conditions, which may wrongly imply that these methods have comparable performances. In this paper, we shed light on some major differences between these two methods. First, we present a class of structured matrix completion problems for which the B-M methods fail with an overwhelming probability, while the SDP method works correctly. Second, we identify a class of highly sparse matrix completion problems for which the B-M method works and the SDP method fails. Third, we prove that although the B-M method exhibits the same performance independent of the rank of the unknown solution, the success of the SDP method is correlated to the rank of the solution and improves as the rank increases. Unlike the existing literature that has mainly focused on those instances of matrix sensing for which both SDP and B-M work, this paper offers the first result on the unique merit of each method over the alternative approach.

Noisy Low-rank Matrix Optimization: Geometry of Local Minima and Convergence Rate

This paper is concerned with low-rank matrix optimization, which has found a wide range of applications in machine learning. This problem in the special case of matrix sense has been studied extensively through the notion of Restricted Isometry Property (RIP), leading to a wealth of results on the geometric landscape of the problem and the convergence rate of common algorithms. However, the existing results are not able to handle the problem with a general objective function subject to noisy data. In this paper, we address this problem by developing a mathematical framework that can deal with random corruptions to general objective functions, where the noise model is arbitrary. We prove that as long as the RIP constant of the noiseless objective is less than $1/3$, any spurious local solution of the noisy optimization problem must be close to the ground truth solution. By working through the strict saddle property, we also show that an approximate solution can be found in polynomial time. We characterize the geometry of the spurious local minima of the problem in a local region around the ground truth in the case when the RIP constant is greater than $1/3$. This paper offers the first set of results on the global and local optimization landscapes of general low-rank optimization problems under arbitrary random corruptions.

Sharp Restricted Isometry Property Bounds for Low-rank Matrix Recovery Problems with Corrupted Measurements

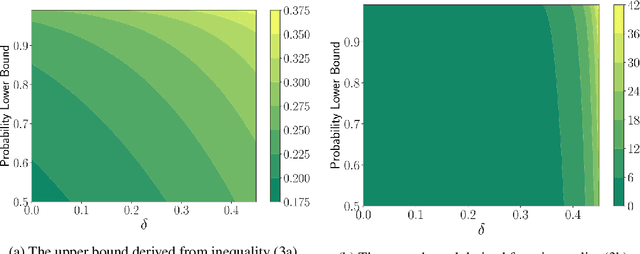
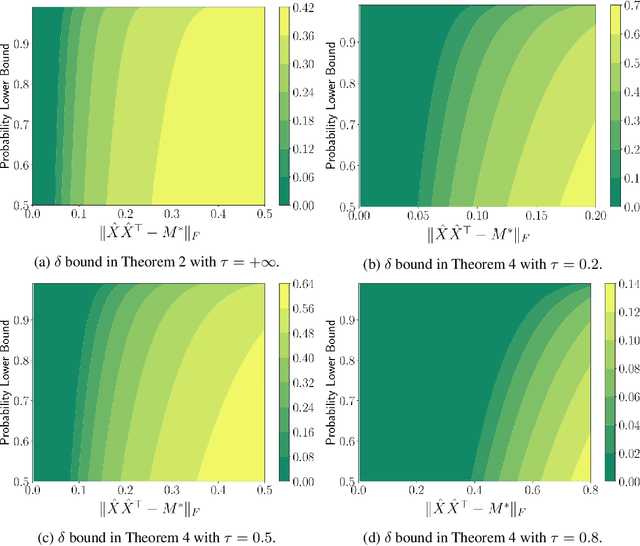
In this paper, we study a general low-rank matrix recovery problem with linear measurements corrupted by some noise. The objective is to understand under what conditions on the restricted isometry property (RIP) of the problem local search methods can find the ground truth with a small error. By analyzing the landscape of the non-convex problem, we first propose a global guarantee on the maximum distance between an arbitrary local minimizer and the ground truth under the assumption that the RIP constant is smaller than 1/2. We show that this distance shrinks to zero as the intensity of the noise reduces. Our new guarantee is sharp in terms of the RIP constant and is much stronger than the existing results. We then present a local guarantee for problems with an arbitrary RIP constant, which states that any local minimizer is either considerably close to the ground truth or far away from it. The developed results demonstrate how the noise intensity and the RIP constant of the problem affect the locations of the local minima relative to the true solution.

Partition-Based Convex Relaxations for Certifying the Robustness of ReLU Neural Networks

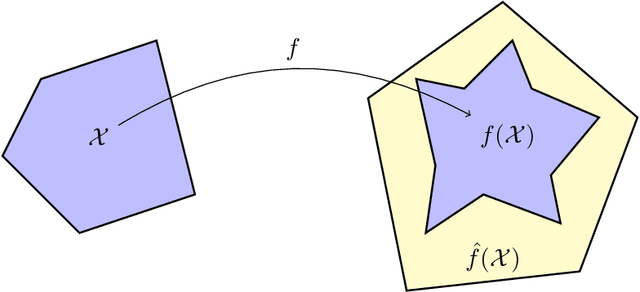
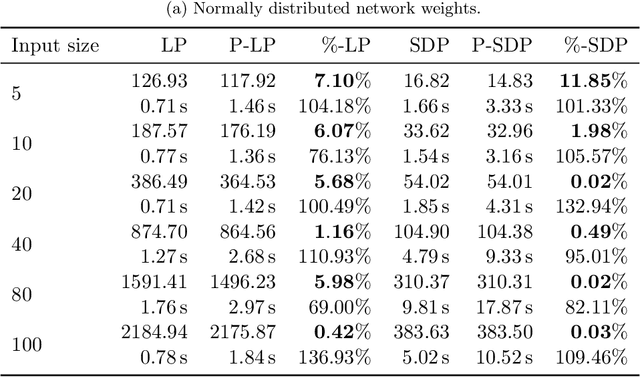
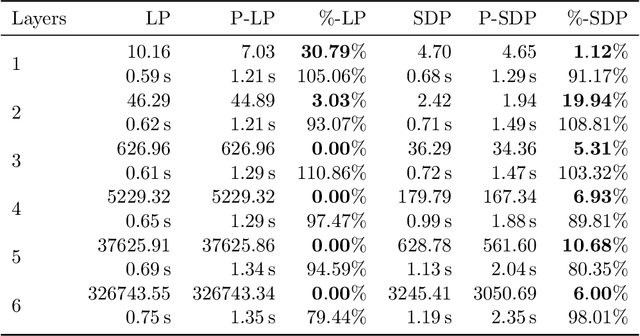
In this paper, we study certifying the robustness of ReLU neural networks against adversarial input perturbations. To diminish the relaxation error suffered by the popular linear programming (LP) and semidefinite programming (SDP) certification methods, we propose partitioning the input uncertainty set and solving the relaxations on each part separately. We show that this approach reduces relaxation error, and that the error is eliminated entirely upon performing an LP relaxation with an intelligently designed partition. To scale this approach to large networks, we consider courser partitions that take the same form as this motivating partition. We prove that computing such a partition that directly minimizes the LP relaxation error is NP-hard. By instead minimizing the worst-case LP relaxation error, we develop a computationally tractable scheme with a closed-form optimal two-part partition. We extend the analysis to the SDP, where the feasible set geometry is exploited to design a two-part partition that minimizes the worst-case SDP relaxation error. Experiments on IRIS classifiers demonstrate significant reduction in relaxation error, offering certificates that are otherwise void without partitioning. By independently increasing the input size and the number of layers, we empirically illustrate under which regimes the partitioned LP and SDP are best applied.

Strengthened SDP Verification of Neural Network Robustness via Non-Convex Cuts

There have been major advances on the design of neural networks, but still they cannot be applied to many safety-critical systems due to the lack of efficient computational techniques to analyze and certify their robustness. Recently, various methods based on convex optimization have been proposed to address this issue. In particular, the semidefinite programming (SDP) approach has gained popularity in convexifying the robustness analysis problem. Since this approach is prone to a large relaxation gap, this paper develops a new technique to reduce the gap by adding non-convex cuts via disjunctive programming. The proposed method amounts to a sequential SDP technique. We analyze the performance of this method both theoretically and empirically, and show that it bridges the gap as the number of cuts increases.

Tightened Convex Relaxations for Neural Network Robustness Certification

In this paper, we consider the problem of certifying the robustness of neural networks to perturbed and adversarial input data. Such certification is imperative for the application of neural networks in safety-critical decision-making and control systems. Certification techniques using convex optimization have been proposed, but they often suffer from relaxation errors that void the certificate. Our work exploits the structure of ReLU networks to improve relaxation errors through a novel partition-based certification procedure. The proposed method is proven to tighten existing linear programming relaxations, and asymptotically achieves zero relaxation error as the partition is made finer. We develop a finite partition that attains zero relaxation error and use the result to derive a tractable partitioning scheme that minimizes the worst-case relaxation error. Experiments using real data show that the partitioning procedure is able to issue robustness certificates in cases where prior methods fail. Consequently, partition-based certification procedures are found to provide an intuitive, effective, and theoretically justified method for tightening existing convex relaxation techniques.

Certifiably Globally Optimal Extrinsic Calibration from Per-Sensor Egomotion

We present a certifiably globally optimal algorithm for determining the extrinsic calibration between two sensors that are capable of producing independent egomotion estimates. This problem has been previously solved using a variety of techniques, including local optimization approaches that have no formal global optimality guarantees. We use a quadratic objective function to formulate calibration as a quadratically constrained quadratic program (QCQP). By leveraging recent advances in the optimization of QCQPs, we are able to use existing semidefinite program (SDP) solvers to obtain a certifiably global optimum via the Lagrangian dual problem. Our problem formulation can be globally optimized by existing general-purpose solvers in less than a second, regardless of the number of measurements available and the noise level. This enables a variety of robotic platforms to rapidly and robustly compute and certify a globally optimal set of calibration parameters without a prior estimate or operator intervention. We compare the performance of our approach with a local solver on extensive simulations and multiple real datasets. Finally, we present necessary observability conditions that connect our approach to recent theoretical results and analytically support the empirical performance of our system.