Escaping Local Minima Provably in Non-convex Matrix Sensing: A Deterministic Framework via Simulated Lifting

Low-rank matrix sensing is a fundamental yet challenging nonconvex problem whose optimization landscape typically contains numerous spurious local minima, making it difficult for gradient-based optimizers to converge to the global optimum. Recent work has shown that over-parameterization via tensor lifting can convert such local minima into strict saddle points, an insight that also partially explains why massive scaling can improve generalization and performance in modern machine learning. Motivated by this observation, we propose a Simulated Oracle Direction (SOD) escape mechanism that simulates the landscape and escape direction of the over-parametrized space, without resorting to actually lifting the problem, since that would be computationally intractable. In essence, we designed a mathematical framework to project over-parametrized escape directions onto the original parameter space to guarantee a strict decrease of objective value from existing local minima. To the best of the our knowledge, this represents the first deterministic framework that could escape spurious local minima with guarantee, especially without using random perturbations or heuristic estimates. Numerical experiments demonstrate that our framework reliably escapes local minima and facilitates convergence to global optima, while incurring minimal computational cost when compared to explicit tensor over-parameterization. We believe this framework has non-trivial implications for nonconvex optimization beyond matrix sensing, by showcasing how simulated over-parameterization can be leveraged to tame challenging optimization landscapes.

Topology-Aware 3D Gaussian Splatting: Leveraging Persistent Homology for Optimized Structural Integrity

Gaussian Splatting (GS) has emerged as a crucial technique for representing discrete volumetric radiance fields. It leverages unique parametrization to mitigate computational demands in scene optimization. This work introduces Topology-Aware 3D Gaussian Splatting (Topology-GS), which addresses two key limitations in current approaches: compromised pixel-level structural integrity due to incomplete initial geometric coverage, and inadequate feature-level integrity from insufficient topological constraints during optimization. To overcome these limitations, Topology-GS incorporates a novel interpolation strategy, Local Persistent Voronoi Interpolation (LPVI), and a topology-focused regularization term based on persistent barcodes, named PersLoss. LPVI utilizes persistent homology to guide adaptive interpolation, enhancing point coverage in low-curvature areas while preserving topological structure. PersLoss aligns the visual perceptual similarity of rendered images with ground truth by constraining distances between their topological features. Comprehensive experiments on three novel-view synthesis benchmarks demonstrate that Topology-GS outperforms existing methods in terms of PSNR, SSIM, and LPIPS metrics, while maintaining efficient memory usage. This study pioneers the integration of topology with 3D-GS, laying the groundwork for future research in this area.

Foresight of Graph Reinforcement Learning Latent Permutations Learnt by Gumbel Sinkhorn Network

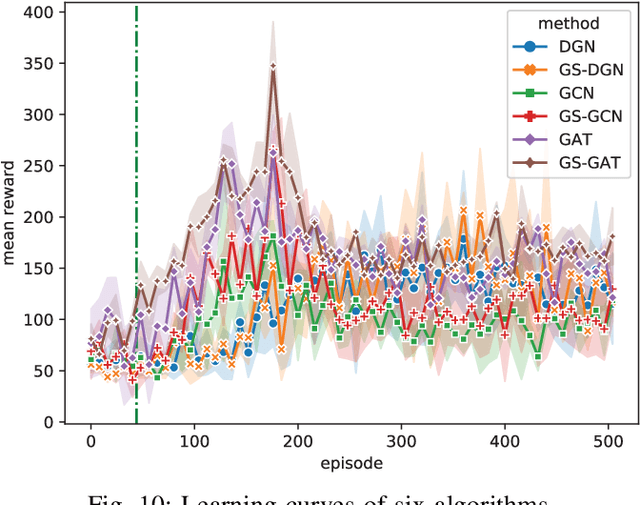
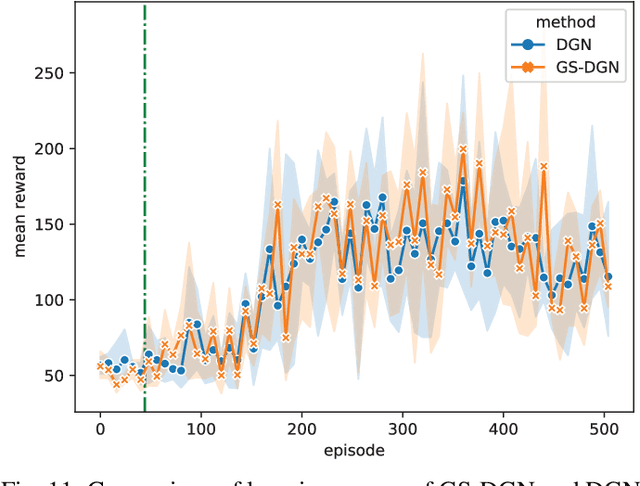
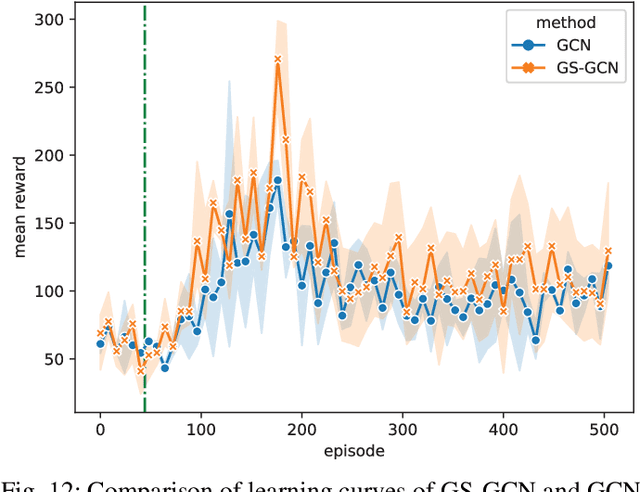
Vital importance has necessity to be attached to cooperation in multi-agent environments, as a result of which some reinforcement learning algorithms combined with graph neural networks have been proposed to understand the mutual interplay between agents. However, highly complicated and dynamic multi-agent environments require more ingenious graph neural networks, which can comprehensively represent not only the graph topology structure but also evolution process of the structure due to agents emerging, disappearing and moving. To tackle these difficulties, we propose Gumbel Sinkhorn graph attention reinforcement learning, where a graph attention network highly represents the underlying graph topology structure of the multi-agent environment, and can adapt to the dynamic topology structure of graph better with the help of Gumbel Sinkhorn network by learning latent permutations. Empirically, simulation results show how our proposed graph reinforcement learning methodology outperforms existing methods in the PettingZoo multi-agent environment by learning latent permutations.