Fast Best-of-N Decoding via Speculative Rejection

The safe and effective deployment of Large Language Models (LLMs) involves a critical step called alignment, which ensures that the model's responses are in accordance with human preferences. Prevalent alignment techniques, such as DPO, PPO and their variants, align LLMs by changing the pre-trained model weights during a phase called post-training. While predominant, these post-training methods add substantial complexity before LLMs can be deployed. Inference-time alignment methods avoid the complex post-training step and instead bias the generation towards responses that are aligned with human preferences. The best-known inference-time alignment method, called Best-of-N, is as effective as the state-of-the-art post-training procedures. Unfortunately, Best-of-N requires vastly more resources at inference time than standard decoding strategies, which makes it computationally not viable. In this work, we introduce Speculative Rejection, a computationally-viable inference-time alignment algorithm. It generates high-scoring responses according to a given reward model, like Best-of-N does, while being between 16 to 32 times more computationally efficient.

ArCHer: Training Language Model Agents via Hierarchical Multi-Turn RL

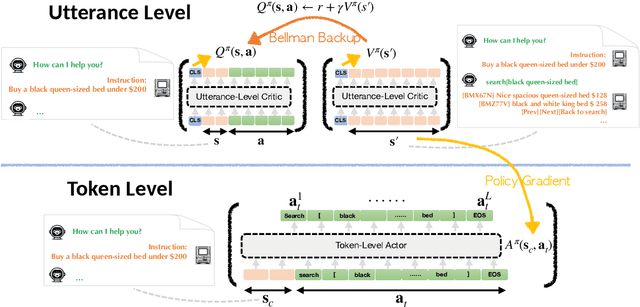
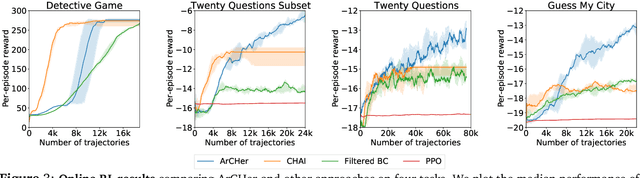
A broad use case of large language models (LLMs) is in goal-directed decision-making tasks (or "agent" tasks), where an LLM needs to not just generate completions for a given prompt, but rather make intelligent decisions over a multi-turn interaction to accomplish a task (e.g., when interacting with the web, using tools, or providing customer support). Reinforcement learning (RL) provides a general paradigm to address such agent tasks, but current RL methods for LLMs largely focus on optimizing single-turn rewards. By construction, most single-turn RL methods cannot endow LLMs with the ability to intelligently seek information over multiple turns, perform credit assignment, or reason about their past actions -- all of which are critical in agent tasks. This raises the question: how can we design effective and efficient multi-turn RL algorithms for LLMs? In this paper, we develop a framework for building multi-turn RL algorithms for fine-tuning LLMs, that preserves the flexibility of existing single-turn RL methods for LLMs (e.g., proximal policy optimization), while accommodating multiple turns, long horizons, and delayed rewards effectively. To do this, our framework adopts a hierarchical RL approach and runs two RL algorithms in parallel: a high-level off-policy value-based RL algorithm to aggregate reward over utterances, and a low-level RL algorithm that utilizes this high-level value function to train a token policy within each utterance or turn. Our hierarchical framework, Actor-Critic Framework with a Hierarchical Structure (ArCHer), can also give rise to other RL methods. Empirically, we find that ArCHer significantly improves efficiency and performance on agent tasks, attaining a sample efficiency of about 100x over existing methods, while also improving with larger model capacity (upto the 7 billion scale that we tested on).

Is Offline Decision Making Possible with Only Few Samples? Reliable Decisions in Data-Starved Bandits via Trust Region Enhancement

What can an agent learn in a stochastic Multi-Armed Bandit (MAB) problem from a dataset that contains just a single sample for each arm? Surprisingly, in this work, we demonstrate that even in such a data-starved setting it may still be possible to find a policy competitive with the optimal one. This paves the way to reliable decision-making in settings where critical decisions must be made by relying only on a handful of samples. Our analysis reveals that \emph{stochastic policies can be substantially better} than deterministic ones for offline decision-making. Focusing on offline multi-armed bandits, we design an algorithm called Trust Region of Uncertainty for Stochastic policy enhancemenT (TRUST) which is quite different from the predominant value-based lower confidence bound approach. Its design is enabled by localization laws, critical radii, and relative pessimism. We prove that its sample complexity is comparable to that of LCB on minimax problems while being substantially lower on problems with very few samples. Finally, we consider an application to offline reinforcement learning in the special case where the logging policies are known.

Policy Finetuning in Reinforcement Learning via Design of Experiments using Offline Data

In some applications of reinforcement learning, a dataset of pre-collected experience is already available but it is also possible to acquire some additional online data to help improve the quality of the policy. However, it may be preferable to gather additional data with a single, non-reactive exploration policy and avoid the engineering costs associated with switching policies. In this paper we propose an algorithm with provable guarantees that can leverage an offline dataset to design a single non-reactive policy for exploration. We theoretically analyze the algorithm and measure the quality of the final policy as a function of the local coverage of the original dataset and the amount of additional data collected.

When is Realizability Sufficient for Off-Policy Reinforcement Learning?

Model-free algorithms for reinforcement learning typically require a condition called Bellman completeness in order to successfully operate off-policy with function approximation, unless additional conditions are met. However, Bellman completeness is a requirement that is much stronger than realizability and that is deemed to be too strong to hold in practice. In this work, we relax this structural assumption and analyze the statistical complexity of off-policy reinforcement learning when only realizability holds for the prescribed function class. We establish finite-sample guarantees for off-policy reinforcement learning that are free of the approximation error term known as inherent Bellman error, and that depend on the interplay of three factors. The first two are well-know: they are the metric entropy of the function class and the concentrability coefficient that represents the cost of learning off-policy. The third factor is new, and it measures the violation of Bellman completeness, namely the mis-alignment between the chosen function class and its image through the Bellman operator. In essence, these error bounds establish that off-policy reinforcement learning remains statistically viable even in absence of Bellman completeness, and characterize the intermediate situation between the favorable Bellman complete setting and the worst-case scenario where exponential lower bounds are in force. Our analysis directly applies to the solution found by temporal difference algorithms when they converge.

Stabilizing Q-learning with Linear Architectures for Provably Efficient Learning

The $Q$-learning algorithm is a simple and widely-used stochastic approximation scheme for reinforcement learning, but the basic protocol can exhibit instability in conjunction with function approximation. Such instability can be observed even with linear function approximation. In practice, tools such as target networks and experience replay appear to be essential, but the individual contribution of each of these mechanisms is not well understood theoretically. This work proposes an exploration variant of the basic $Q$-learning protocol with linear function approximation. Our modular analysis illustrates the role played by each algorithmic tool that we adopt: a second order update rule, a set of target networks, and a mechanism akin to experience replay. Together, they enable state of the art regret bounds on linear MDPs while preserving the most prominent feature of the algorithm, namely a space complexity independent of the number of step elapsed. We show that the performance of the algorithm degrades very gracefully under a novel and more permissive notion of approximation error. The algorithm also exhibits a form of instance-dependence, in that its performance depends on the "effective" feature dimension.

Bellman Residual Orthogonalization for Offline Reinforcement Learning

We introduce a new reinforcement learning principle that approximates the Bellman equations by enforcing their validity only along an user-defined space of test functions. Focusing on applications to model-free offline RL with function approximation, we exploit this principle to derive confidence intervals for off-policy evaluation, as well as to optimize over policies within a prescribed policy class. We prove an oracle inequality on our policy optimization procedure in terms of a trade-off between the value and uncertainty of an arbitrary comparator policy. Different choices of test function spaces allow us to tackle different problems within a common framework. We characterize the loss of efficiency in moving from on-policy to off-policy data using our procedures, and establish connections to concentrability coefficients studied in past work. We examine in depth the implementation of our methods with linear function approximation, and provide theoretical guarantees with polynomial-time implementations even when Bellman closure does not hold.

Provable Benefits of Actor-Critic Methods for Offline Reinforcement Learning

Actor-critic methods are widely used in offline reinforcement learning practice, but are not so well-understood theoretically. We propose a new offline actor-critic algorithm that naturally incorporates the pessimism principle, leading to several key advantages compared to the state of the art. The algorithm can operate when the Bellman evaluation operator is closed with respect to the action value function of the actor's policies; this is a more general setting than the low-rank MDP model. Despite the added generality, the procedure is computationally tractable as it involves the solution of a sequence of second-order programs. We prove an upper bound on the suboptimality gap of the policy returned by the procedure that depends on the data coverage of any arbitrary, possibly data dependent comparator policy. The achievable guarantee is complemented with a minimax lower bound that is matching up to logarithmic factors.

Design of Experiments for Stochastic Contextual Linear Bandits

In the stochastic linear contextual bandit setting there exist several minimax procedures for exploration with policies that are reactive to the data being acquired. In practice, there can be a significant engineering overhead to deploy these algorithms, especially when the dataset is collected in a distributed fashion or when a human in the loop is needed to implement a different policy. Exploring with a single non-reactive policy is beneficial in such cases. Assuming some batch contexts are available, we design a single stochastic policy to collect a good dataset from which a near-optimal policy can be extracted. We present a theoretical analysis as well as numerical experiments on both synthetic and real-world datasets.

Cautiously Optimistic Policy Optimization and Exploration with Linear Function Approximation

Policy optimization methods are popular reinforcement learning algorithms, because their incremental and on-policy nature makes them more stable than the value-based counterparts. However, the same properties also make them slow to converge and sample inefficient, as the on-policy requirement precludes data reuse and the incremental updates couple large iteration complexity into the sample complexity. These characteristics have been observed in experiments as well as in theory in the recent work of~\citet{agarwal2020pc}, which provides a policy optimization method PCPG that can robustly find near optimal polices for approximately linear Markov decision processes but suffers from an extremely poor sample complexity compared with value-based techniques. In this paper, we propose a new algorithm, COPOE, that overcomes the sample complexity issue of PCPG while retaining its robustness to model misspecification. Compared with PCPG, COPOE makes several important algorithmic enhancements, such as enabling data reuse, and uses more refined analysis techniques, which we expect to be more broadly applicable to designing new reinforcement learning algorithms. The result is an improvement in sample complexity from $\widetilde{O}(1/\epsilon^{11})$ for PCPG to $\widetilde{O}(1/\epsilon^3)$ for PCPG, nearly bridging the gap with value-based techniques.