A Reinforcement Learning Approach to Estimating Long-term Treatment Effects

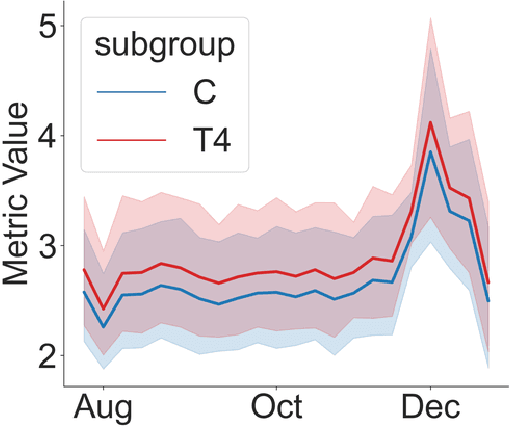
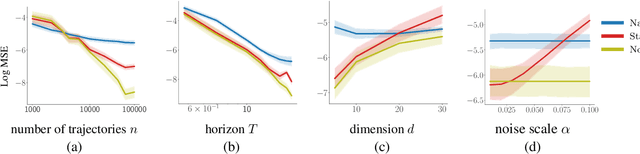
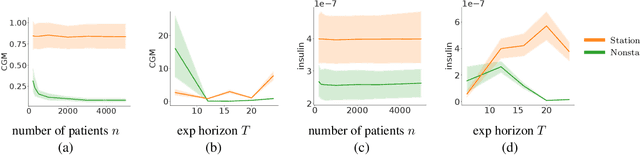
Randomized experiments (a.k.a. A/B tests) are a powerful tool for estimating treatment effects, to inform decisions making in business, healthcare and other applications. In many problems, the treatment has a lasting effect that evolves over time. A limitation with randomized experiments is that they do not easily extend to measure long-term effects, since running long experiments is time-consuming and expensive. In this paper, we take a reinforcement learning (RL) approach that estimates the average reward in a Markov process. Motivated by real-world scenarios where the observed state transition is nonstationary, we develop a new algorithm for a class of nonstationary problems, and demonstrate promising results in two synthetic datasets and one online store dataset.

Split Localized Conformal Prediction

Conformal prediction is a simple and powerful tool that can quantify uncertainty without any distributional assumptions. However, existing methods can only provide an average coverage guarantee, which is not ideal compared to the stronger conditional coverage guarantee. Although achieving exact conditional coverage is proven to be impossible, approximating conditional coverage is still an important research direction. In this paper, we propose a modified non-conformity score by leveraging local approximation of the conditional distribution. The modified score inherits the spirit of split conformal methods, which is simple and efficient compared with full conformal methods but better approximates conditional coverage guarantee. Empirical results on various datasets, including a high dimension age regression on image, demonstrate that our method provides tighter intervals compared to existing methods.

Robust Imitation Learning from Corrupted Demonstrations

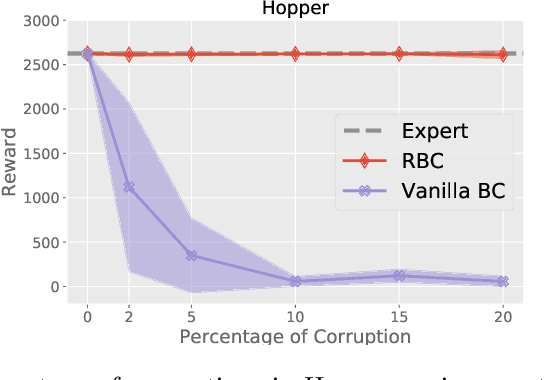
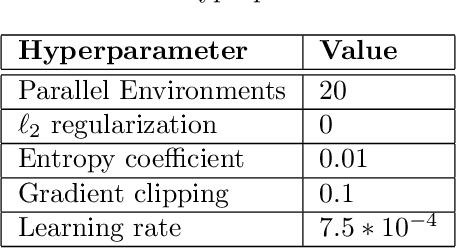
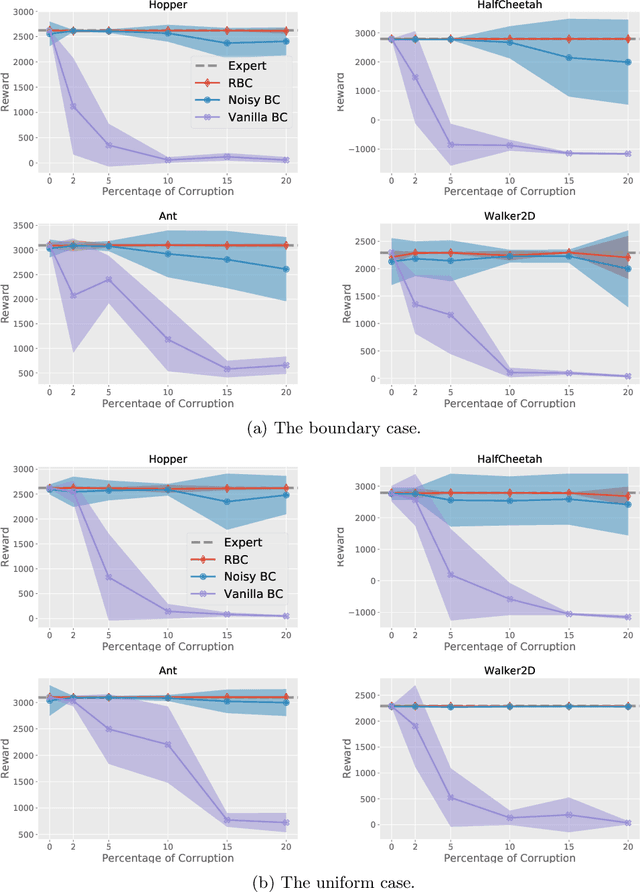
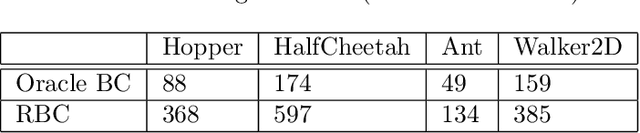
We consider offline Imitation Learning from corrupted demonstrations where a constant fraction of data can be noise or even arbitrary outliers. Classical approaches such as Behavior Cloning assumes that demonstrations are collected by an presumably optimal expert, hence may fail drastically when learning from corrupted demonstrations. We propose a novel robust algorithm by minimizing a Median-of-Means (MOM) objective which guarantees the accurate estimation of policy, even in the presence of constant fraction of outliers. Our theoretical analysis shows that our robust method in the corrupted setting enjoys nearly the same error scaling and sample complexity guarantees as the classical Behavior Cloning in the expert demonstration setting. Our experiments on continuous-control benchmarks validate that our method exhibits the predicted robustness and effectiveness, and achieves competitive results compared to existing imitation learning methods.

Operator Deep Q-Learning: Zero-Shot Reward Transferring in Reinforcement Learning

Reinforcement learning (RL) has drawn increasing interests in recent years due to its tremendous success in various applications. However, standard RL algorithms can only be applied for single reward function, and cannot adapt to an unseen reward function quickly. In this paper, we advocate a general operator view of reinforcement learning, which enables us to directly approximate the operator that maps from reward function to value function. The benefit of learning the operator is that we can incorporate any new reward function as input and attain its corresponding value function in a zero-shot manner. To approximate this special type of operator, we design a number of novel operator neural network architectures based on its theoretical properties. Our design of operator networks outperform the existing methods and the standard design of general purpose operator network, and we demonstrate the benefit of our operator deep Q-learning framework in several tasks including reward transferring for offline policy evaluation (OPE) and reward transferring for offline policy optimization in a range of tasks.

Non-asymptotic Confidence Intervals of Off-policy Evaluation: Primal and Dual Bounds

Off-policy evaluation (OPE) is the task of estimating the expected reward of a given policy based on offline data previously collected under different policies. Therefore, OPE is a key step in applying reinforcement learning to real-world domains such as medical treatment, where interactive data collection is expensive or even unsafe. As the observed data tends to be noisy and limited, it is essential to provide rigorous uncertainty quantification, not just a point estimation, when applying OPE to make high stakes decisions. This work considers the problem of constructing non-asymptotic confidence intervals in infinite-horizon off-policy evaluation, which remains a challenging open question. We develop a practical algorithm through a primal-dual optimization-based approach, which leverages the kernel Bellman loss (KBL) of Feng et al.(2019) and a new martingale concentration inequality of KBL applicable to time-dependent data with unknown mixing conditions. Our algorithm makes minimum assumptions on the data and the function class of the Q-function, and works for the behavior-agnostic settings where the data is collected under a mix of arbitrary unknown behavior policies. We present empirical results that clearly demonstrate the advantages of our approach over existing methods.

Off-Policy Interval Estimation with Lipschitz Value Iteration

Off-policy evaluation provides an essential tool for evaluating the effects of different policies or treatments using only observed data. When applied to high-stakes scenarios such as medical diagnosis or financial decision-making, it is crucial to provide provably correct upper and lower bounds of the expected reward, not just a classical single point estimate, to the end-users, as executing a poor policy can be very costly. In this work, we propose a provably correct method for obtaining interval bounds for off-policy evaluation in a general continuous setting. The idea is to search for the maximum and minimum values of the expected reward among all the Lipschitz Q-functions that are consistent with the observations, which amounts to solving a constrained optimization problem on a Lipschitz function space. We go on to introduce a Lipschitz value iteration method to monotonically tighten the interval, which is simple yet efficient and provably convergent. We demonstrate the practical efficiency of our method on a range of benchmarks.

Accountable Off-Policy Evaluation With Kernel Bellman Statistics

We consider off-policy evaluation (OPE), which evaluates the performance of a new policy from observed data collected from previous experiments, without requiring the execution of the new policy. This finds important applications in areas with high execution cost or safety concerns, such as medical diagnosis, recommendation systems and robotics. In practice, due to the limited information from off-policy data, it is highly desirable to construct rigorous confidence intervals, not just point estimation, for the policy performance. In this work, we propose a new variational framework which reduces the problem of calculating tight confidence bounds in OPE into an optimization problem on a feasible set that catches the true state-action value function with high probability. The feasible set is constructed by leveraging statistical properties of a recently proposed kernel Bellman loss (Feng et al., 2019). We design an efficient computational approach for calculating our bounds, and extend it to perform post-hoc diagnosis and correction for existing estimators. Empirical results show that our method yields tight confidence intervals in different settings.

PENet: Object Detection using Points Estimation in Aerial Images

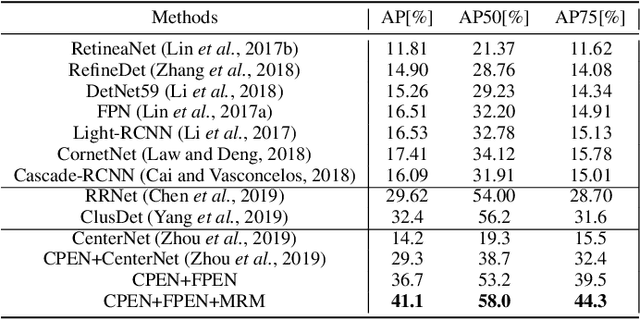
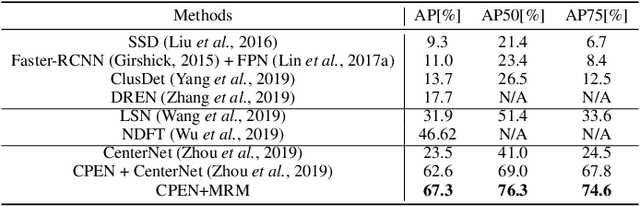
Aerial imagery has been increasingly adopted in mission-critical tasks, such as traffic surveillance, smart cities, and disaster assistance. However, identifying objects from aerial images faces the following challenges: 1) objects of interests are often too small and too dense relative to the images; 2) objects of interests are often in different relative sizes; and 3) the number of objects in each category is imbalanced. A novel network structure, Points Estimated Network (PENet), is proposed in this work to answer these challenges. PENet uses a Mask Resampling Module (MRM) to augment the imbalanced datasets, a coarse anchor-free detector (CPEN) to effectively predict the center points of the small object clusters, and a fine anchor-free detector FPEN to locate the precise positions of the small objects. An adaptive merge algorithm Non-maximum Merge (NMM) is implemented in CPEN to address the issue of detecting dense small objects, and a hierarchical loss is defined in FPEN to further improve the classification accuracy. Our extensive experiments on aerial datasets visDrone and UAVDT showed that PENet achieved higher precision results than existing state-of-the-art approaches. Our best model achieved 8.7% improvement on visDrone and 20.3% on UAVDT.

Stein Variational Gradient Descent With Matrix-Valued Kernels

Stein variational gradient descent (SVGD) is a particle-based inference algorithm that leverages gradient information for efficient approximate inference. In this work, we enhance SVGD by leveraging preconditioning matrices, such as the Hessian and Fisher information matrix, to incorporate geometric information into SVGD updates. We achieve this by presenting a generalization of SVGD that replaces the scalar-valued kernels in vanilla SVGD with more general matrix-valued kernels. This yields a significant extension of SVGD, and more importantly, allows us to flexibly incorporate various preconditioning matrices to accelerate the exploration in the probability landscape. Empirical results show that our method outperforms vanilla SVGD and a variety of baseline approaches over a range of real-world Bayesian inference tasks.