Towards Agentic Recommender Systems in the Era of Multimodal Large Language Models

Recent breakthroughs in Large Language Models (LLMs) have led to the emergence of agentic AI systems that extend beyond the capabilities of standalone models. By empowering LLMs to perceive external environments, integrate multimodal information, and interact with various tools, these agentic systems exhibit greater autonomy and adaptability across complex tasks. This evolution brings new opportunities to recommender systems (RS): LLM-based Agentic RS (LLM-ARS) can offer more interactive, context-aware, and proactive recommendations, potentially reshaping the user experience and broadening the application scope of RS. Despite promising early results, fundamental challenges remain, including how to effectively incorporate external knowledge, balance autonomy with controllability, and evaluate performance in dynamic, multimodal settings. In this perspective paper, we first present a systematic analysis of LLM-ARS: (1) clarifying core concepts and architectures; (2) highlighting how agentic capabilities -- such as planning, memory, and multimodal reasoning -- can enhance recommendation quality; and (3) outlining key research questions in areas such as safety, efficiency, and lifelong personalization. We also discuss open problems and future directions, arguing that LLM-ARS will drive the next wave of RS innovation. Ultimately, we foresee a paradigm shift toward intelligent, autonomous, and collaborative recommendation experiences that more closely align with users' evolving needs and complex decision-making processes.

Provable Zero-Shot Generalization in Offline Reinforcement Learning

In this work, we study offline reinforcement learning (RL) with zero-shot generalization property (ZSG), where the agent has access to an offline dataset including experiences from different environments, and the goal of the agent is to train a policy over the training environments which performs well on test environments without further interaction. Existing work showed that classical offline RL fails to generalize to new, unseen environments. We propose pessimistic empirical risk minimization (PERM) and pessimistic proximal policy optimization (PPPO), which leverage pessimistic policy evaluation to guide policy learning and enhance generalization. We show that both PERM and PPPO are capable of finding a near-optimal policy with ZSG. Our result serves as a first step in understanding the foundation of the generalization phenomenon in offline reinforcement learning.

Breaking the $\log(1/Δ_2)$ Barrier: Better Batched Best Arm Identification with Adaptive Grids

We investigate the problem of batched best arm identification in multi-armed bandits, where we aim to identify the best arm from a set of $n$ arms while minimizing both the number of samples and batches. We introduce an algorithm that achieves near-optimal sample complexity and features an instance-sensitive batch complexity, which breaks the $\log(1/\Delta_2)$ barrier. The main contribution of our algorithm is a novel sample allocation scheme that effectively balances exploration and exploitation for batch sizes. Experimental results indicate that our approach is more batch-efficient across various setups. We also extend this framework to the problem of batched best arm identification in linear bandits and achieve similar improvements.

Return Augmented Decision Transformer for Off-Dynamics Reinforcement Learning

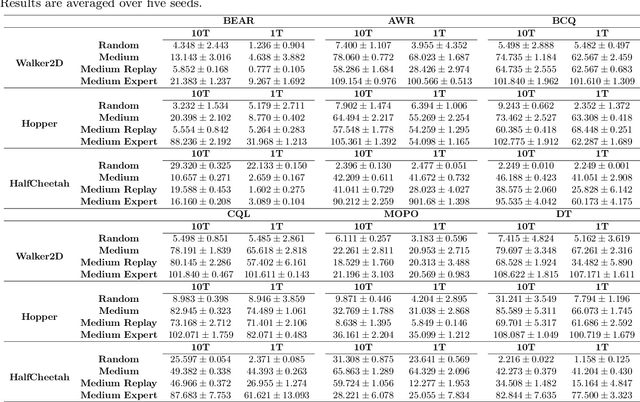
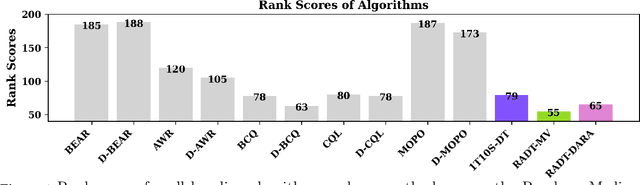
We study offline off-dynamics reinforcement learning (RL) to utilize data from an easily accessible source domain to enhance policy learning in a target domain with limited data. Our approach centers on return-conditioned supervised learning (RCSL), particularly focusing on the decision transformer (DT), which can predict actions conditioned on desired return guidance and complete trajectory history. Previous works tackle the dynamics shift problem by augmenting the reward in the trajectory from the source domain to match the optimal trajectory in the target domain. However, this strategy can not be directly applicable in RCSL owing to (1) the unique form of the RCSL policy class, which explicitly depends on the return, and (2) the absence of a straightforward representation of the optimal trajectory distribution. We propose the Return Augmented Decision Transformer (RADT) method, where we augment the return in the source domain by aligning its distribution with that in the target domain. We provide the theoretical analysis demonstrating that the RCSL policy learned from RADT achieves the same level of suboptimality as would be obtained without a dynamics shift. We introduce two practical implementations RADT-DARA and RADT-MV respectively. Extensive experiments conducted on D4RL datasets reveal that our methods generally outperform dynamic programming based methods in off-dynamics RL scenarios.

CoPS: Empowering LLM Agents with Provable Cross-Task Experience Sharing

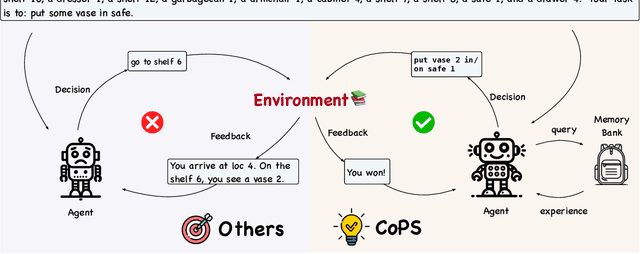
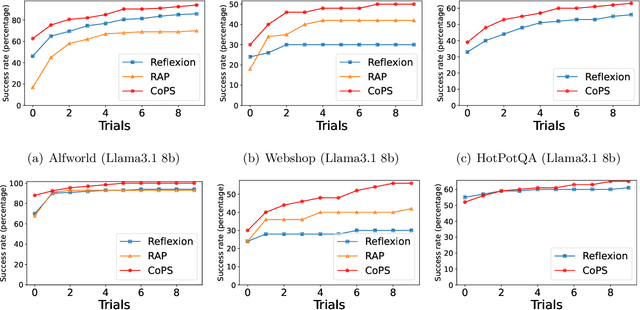
Sequential reasoning in agent systems has been significantly advanced by large language models (LLMs), yet existing approaches face limitations. Reflection-driven reasoning relies solely on knowledge in pretrained models, limiting performance in novel scenarios, while experience-assisted reasoning often depends on external experiences and lacks clear principles for selecting representative experiences. We address these limitations by proposing CoPS (Cross-Task Experience Sharing), a generalizable algorithm that enhances sequential reasoning by cross-task experience sharing and selection. In detail, CoPS leverages agents' experiences on previous tasks, selecting distribution-matched experiences via a provable pessimism-based strategy to maximize utility while minimizing risks from distribution shifts. Extensive experimental results on benchmarks like Alfworld, Webshop, and HotPotQA demonstrate that CoPS consistently outperforms state-of-the-art baselines, with superior sample efficiency suitable for resource-constrained scenarios. Theoretically, we show that the performance of our algorithm depends on both the quality of the pretrained LLM and the matching between the agent's task-dependent trial distribution and that generated by the LLM. Our work bridges the gap between existing sequential reasoning paradigms and validates the effectiveness of leveraging cross-task experiences, shedding light on the potential to improve agents' generalization and adaptability across diverse tasks. Our codes are available at $\href{https://github.com/uclaml/COPS}{\text{https://github.com/uclaml/COPS}}$.

Model-based RL as a Minimalist Approach to Horizon-Free and Second-Order Bounds

Learning a transition model via Maximum Likelihood Estimation (MLE) followed by planning inside the learned model is perhaps the most standard and simplest Model-based Reinforcement Learning (RL) framework. In this work, we show that such a simple Model-based RL scheme, when equipped with optimistic and pessimistic planning procedures, achieves strong regret and sample complexity bounds in online and offline RL settings. Particularly, we demonstrate that under the conditions where the trajectory-wise reward is normalized between zero and one and the transition is time-homogenous, it achieves horizon-free and second-order bounds. Horizon-free means that our bounds have no polynomial dependence on the horizon of the Markov Decision Process. A second-order bound is a type of instance-dependent bound that scales with respect to the variances of the returns of the policies which can be small when the system is nearly deterministic and (or) the optimal policy has small values. We highlight that our algorithms are simple, fairly standard, and indeed have been extensively studied in the RL literature: they learn a model via MLE, build a version space around the MLE solution, and perform optimistic or pessimistic planning depending on whether operating in the online or offline mode. These algorithms do not rely on additional specialized algorithmic designs such as learning variances and performing variance-weighted learning and thus can leverage rich function approximations that are significantly beyond linear or tabular structures. The simplicity of the algorithms also implies that our horizon-free and second-order regret analysis is actually standard and mainly follows the general framework of optimism/pessimism in the face of uncertainty.

Uncertainty-Aware Reward-Free Exploration with General Function Approximation

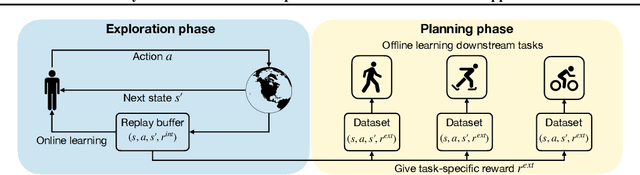
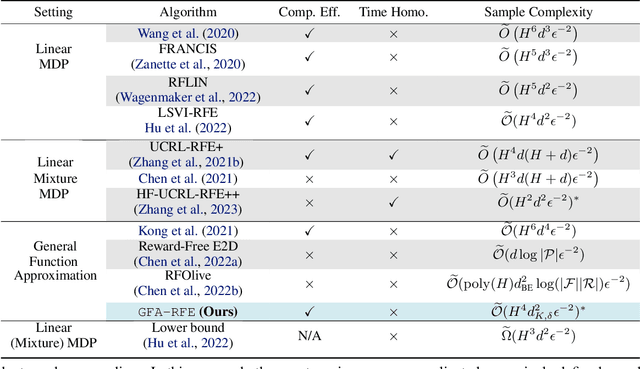
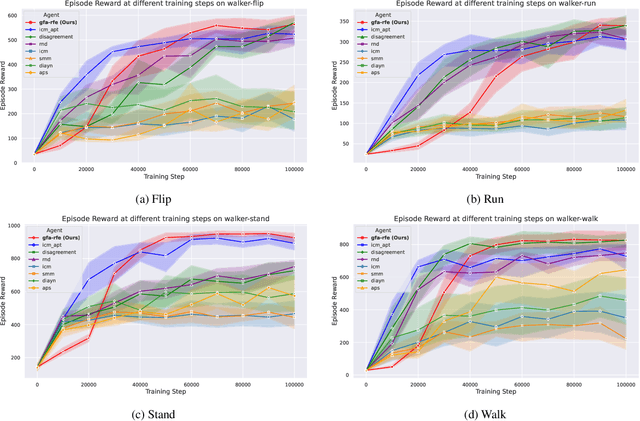
Mastering multiple tasks through exploration and learning in an environment poses a significant challenge in reinforcement learning (RL). Unsupervised RL has been introduced to address this challenge by training policies with intrinsic rewards rather than extrinsic rewards. However, current intrinsic reward designs and unsupervised RL algorithms often overlook the heterogeneous nature of collected samples, thereby diminishing their sample efficiency. To overcome this limitation, in this paper, we propose a reward-free RL algorithm called \alg. The key idea behind our algorithm is an uncertainty-aware intrinsic reward for exploring the environment and an uncertainty-weighted learning process to handle heterogeneous uncertainty in different samples. Theoretically, we show that in order to find an $\epsilon$-optimal policy, GFA-RFE needs to collect $\tilde{O} (H^2 \log N_{\mathcal F} (\epsilon) \mathrm{dim} (\mathcal F) / \epsilon^2 )$ number of episodes, where $\mathcal F$ is the value function class with covering number $N_{\mathcal F} (\epsilon)$ and generalized eluder dimension $\mathrm{dim} (\mathcal F)$. Such a result outperforms all existing reward-free RL algorithms. We further implement and evaluate GFA-RFE across various domains and tasks in the DeepMind Control Suite. Experiment results show that GFA-RFE outperforms or is comparable to the performance of state-of-the-art unsupervised RL algorithms.

Variance-Dependent Regret Bounds for Non-stationary Linear Bandits

We investigate the non-stationary stochastic linear bandit problem where the reward distribution evolves each round. Existing algorithms characterize the non-stationarity by the total variation budget $B_K$, which is the summation of the change of the consecutive feature vectors of the linear bandits over $K$ rounds. However, such a quantity only measures the non-stationarity with respect to the expectation of the reward distribution, which makes existing algorithms sub-optimal under the general non-stationary distribution setting. In this work, we propose algorithms that utilize the variance of the reward distribution as well as the $B_K$, and show that they can achieve tighter regret upper bounds. Specifically, we introduce two novel algorithms: Restarted Weighted$\text{OFUL}^+$ and Restarted $\text{SAVE}^+$. These algorithms address cases where the variance information of the rewards is known and unknown, respectively. Notably, when the total variance $V_K$ is much smaller than $K$, our algorithms outperform previous state-of-the-art results on non-stationary stochastic linear bandits under different settings. Experimental evaluations further validate the superior performance of our proposed algorithms over existing works.

DPAdapter: Improving Differentially Private Deep Learning through Noise Tolerance Pre-training

Recent developments have underscored the critical role of \textit{differential privacy} (DP) in safeguarding individual data for training machine learning models. However, integrating DP oftentimes incurs significant model performance degradation due to the perturbation introduced into the training process, presenting a formidable challenge in the {differentially private machine learning} (DPML) field. To this end, several mitigative efforts have been proposed, typically revolving around formulating new DPML algorithms or relaxing DP definitions to harmonize with distinct contexts. In spite of these initiatives, the diminishment induced by DP on models, particularly large-scale models, remains substantial and thus, necessitates an innovative solution that adeptly circumnavigates the consequential impairment of model utility. In response, we introduce DPAdapter, a pioneering technique designed to amplify the model performance of DPML algorithms by enhancing parameter robustness. The fundamental intuition behind this strategy is that models with robust parameters are inherently more resistant to the noise introduced by DP, thereby retaining better performance despite the perturbations. DPAdapter modifies and enhances the sharpness-aware minimization (SAM) technique, utilizing a two-batch strategy to provide a more accurate perturbation estimate and an efficient gradient descent, thereby improving parameter robustness against noise. Notably, DPAdapter can act as a plug-and-play component and be combined with existing DPML algorithms to further improve their performance. Our experiments show that DPAdapter vastly enhances state-of-the-art DPML algorithms, increasing average accuracy from 72.92\% to 77.09\% with a privacy budget of $\epsilon=4$.

Nearly Minimax Optimal Regret for Learning Linear Mixture Stochastic Shortest Path

We study the Stochastic Shortest Path (SSP) problem with a linear mixture transition kernel, where an agent repeatedly interacts with a stochastic environment and seeks to reach certain goal state while minimizing the cumulative cost. Existing works often assume a strictly positive lower bound of the cost function or an upper bound of the expected length for the optimal policy. In this paper, we propose a new algorithm to eliminate these restrictive assumptions. Our algorithm is based on extended value iteration with a fine-grained variance-aware confidence set, where the variance is estimated recursively from high-order moments. Our algorithm achieves an $\tilde{\mathcal O}(dB_*\sqrt{K})$ regret bound, where $d$ is the dimension of the feature mapping in the linear transition kernel, $B_*$ is the upper bound of the total cumulative cost for the optimal policy, and $K$ is the number of episodes. Our regret upper bound matches the $\Omega(dB_*\sqrt{K})$ lower bound of linear mixture SSPs in Min et al. (2022), which suggests that our algorithm is nearly minimax optimal.