Junkai Zhang
An Accelerated Mixed Weighted-Unweighted MMSE Approach for MU-MIMO Beamforming
Oct 23, 2025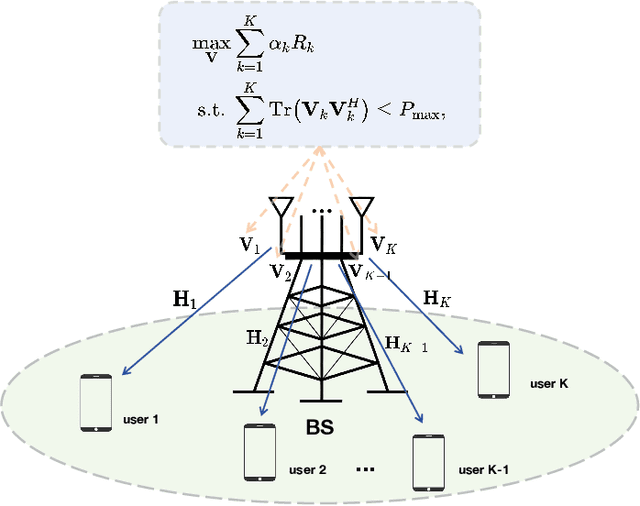
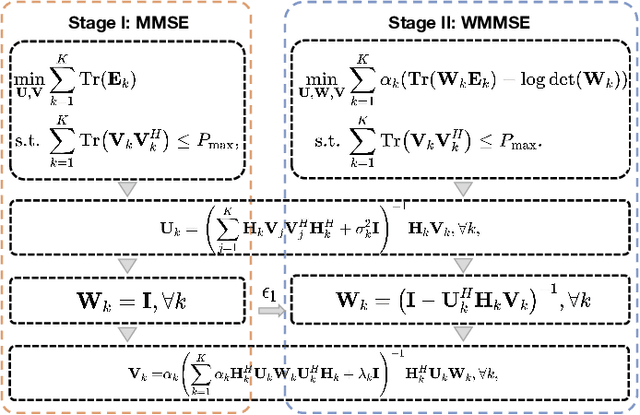
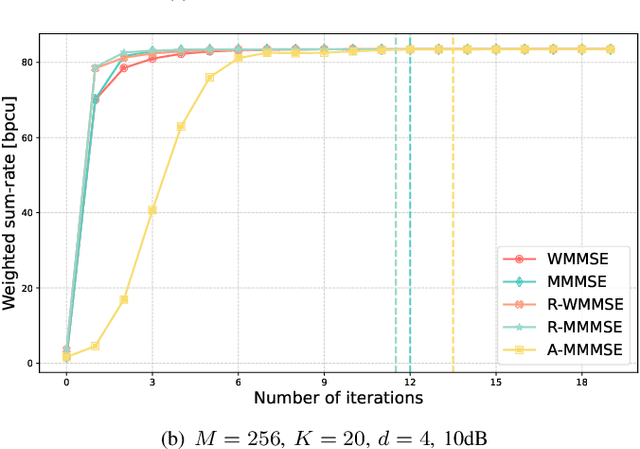
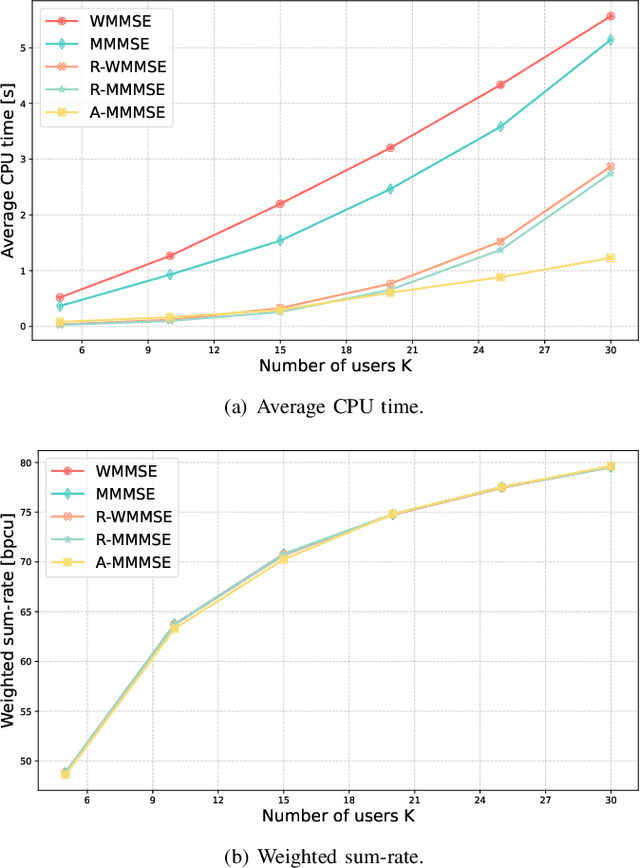
Abstract:Precoding design based on weighted sum-rate (WSR) maximization is a fundamental problem in downlink multi-user multiple-input multiple-output (MU-MIMO) systems. While the weighted minimum mean-square error (WMMSE) algorithm is a standard solution, its high computational complexity--cubic in the number of base station antennas due to matrix inversions--hinders its application in latency-sensitive scenarios. To address this limitation, we propose a highly parallel algorithm based on a block coordinate descent framework. Our key innovation lies in updating the precoding matrix via block coordinate gradient descent, which avoids matrix inversions and relies solely on matrix multiplications, making it exceptionally amenable to GPU acceleration. We prove that the proposed algorithm converges to a stationary point of the WSR maximization problem. Furthermore, we introduce a two-stage warm-start strategy grounded in the sum mean-square error (MSE) minimization problem to accelerate convergence. We refer to our method as the Accelerated Mixed weighted-unweighted sum-MSE minimization (A-MMMSE) algorithm. Simulation results demonstrate that A-MMMSE matches the WSR performance of both conventional WMMSE and its enhanced variant, reduced-WMMSE, while achieving a substantial reduction in computational time across diverse system configurations.
HyP-ASO: A Hybrid Policy-based Adaptive Search Optimization Framework for Large-Scale Integer Linear Programs
Sep 19, 2025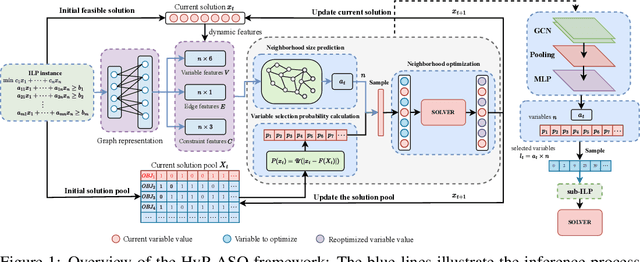

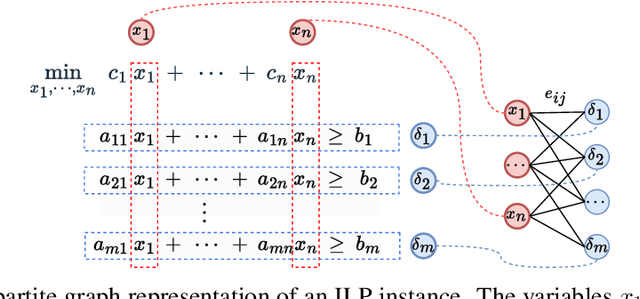
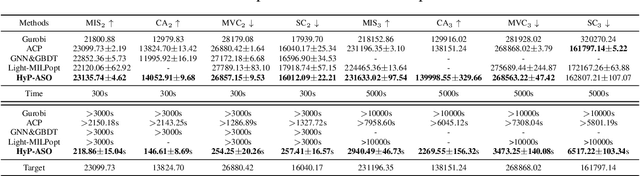
Abstract:Directly solving large-scale Integer Linear Programs (ILPs) using traditional solvers is slow due to their NP-hard nature. While recent frameworks based on Large Neighborhood Search (LNS) can accelerate the solving process, their performance is often constrained by the difficulty in generating sufficiently effective neighborhoods. To address this challenge, we propose HyP-ASO, a hybrid policy-based adaptive search optimization framework that combines a customized formula with deep Reinforcement Learning (RL). The formula leverages feasible solutions to calculate the selection probabilities for each variable in the neighborhood generation process, and the RL policy network predicts the neighborhood size. Extensive experiments demonstrate that HyP-ASO significantly outperforms existing LNS-based approaches for large-scale ILPs. Additional experiments show it is lightweight and highly scalable, making it well-suited for solving large-scale ILPs.
WebSailor: Navigating Super-human Reasoning for Web Agent
Jul 03, 2025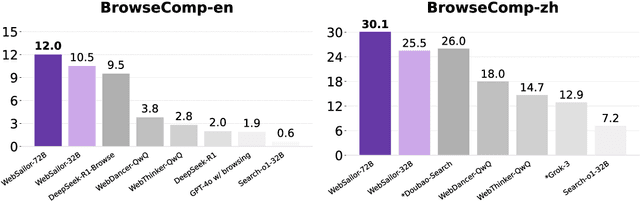
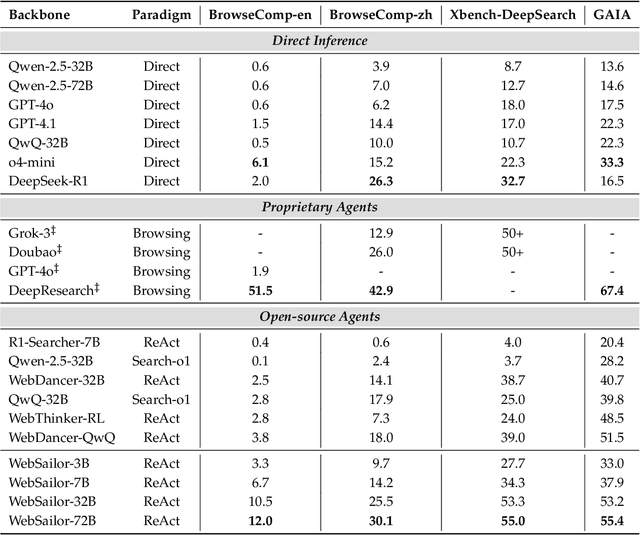
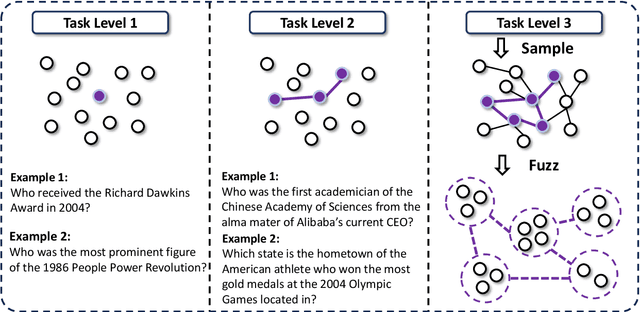

Abstract:Transcending human cognitive limitations represents a critical frontier in LLM training. Proprietary agentic systems like DeepResearch have demonstrated superhuman capabilities on extremely complex information-seeking benchmarks such as BrowseComp, a feat previously unattainable. We posit that their success hinges on a sophisticated reasoning pattern absent in open-source models: the ability to systematically reduce extreme uncertainty when navigating vast information landscapes. Based on this insight, we introduce WebSailor, a complete post-training methodology designed to instill this crucial capability. Our approach involves generating novel, high-uncertainty tasks through structured sampling and information obfuscation, RFT cold start, and an efficient agentic RL training algorithm, Duplicating Sampling Policy Optimization (DUPO). With this integrated pipeline, WebSailor significantly outperforms all opensource agents in complex information-seeking tasks, matching proprietary agents' performance and closing the capability gap.
Adaptive Implicit-Based Deep Learning Channel Estimation for 6G Communications
May 23, 2025Abstract:With the widespread deployment of fifth-generation (5G) wireless networks, research on sixth-generation (6G) technology is gaining momentum. Artificial Intelligence (AI) is anticipated to play a significant role in 6G, particularly through integration with the physical layer for tasks such as channel estimation. Considering resource limitations in real systems, the AI algorithm should be designed to have the ability to balance the accuracy and resource consumption according to the scenarios dynamically. However, conventional explicit multilayer-stacked Deep Learning (DL) models struggle to adapt due to their heavy reliance on the structure of deep neural networks. This article proposes an adaptive Implicit-layer DL Channel Estimation Network (ICENet) with a lightweight framework for vehicle-to-everything communications. This novel approach balances computational complexity and channel estimation accuracy by dynamically adjusting computational resources based on input data conditions, such as channel quality. Unlike explicit multilayer-stacked DL-based channel estimation models, ICENet offers a flexible framework, where specific requirements can be achieved by adaptively changing the number of iterations of the iterative layer. Meanwhile, ICENet requires less memory while maintaining high performance. The article concludes by highlighting open research challenges and promising future research directions.
Hierarchical Modeling for Medical Visual Question Answering with Cross-Attention Fusion
Apr 10, 2025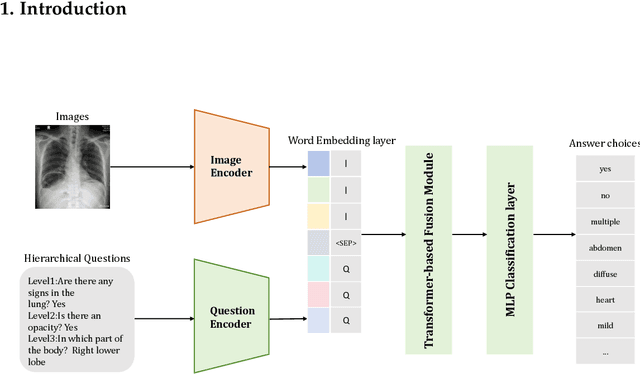
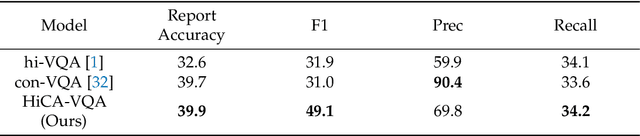
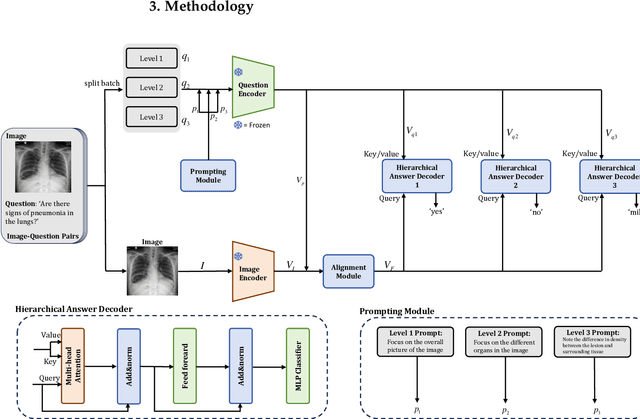
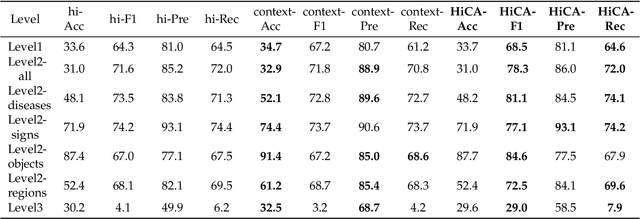
Abstract:Medical Visual Question Answering (Med-VQA) answers clinical questions using medical images, aiding diagnosis. Designing the MedVQA system holds profound importance in assisting clinical diagnosis and enhancing diagnostic accuracy. Building upon this foundation, Hierarchical Medical VQA extends Medical VQA by organizing medical questions into a hierarchical structure and making level-specific predictions to handle fine-grained distinctions. Recently, many studies have proposed hierarchical MedVQA tasks and established datasets, However, several issues still remain: (1) imperfect hierarchical modeling leads to poor differentiation between question levels causing semantic fragmentation across hierarchies. (2) Excessive reliance on implicit learning in Transformer-based cross-modal self-attention fusion methods, which obscures crucial local semantic correlations in medical scenarios. To address these issues, this study proposes a HiCA-VQA method, including two modules: Hierarchical Prompting for fine-grained medical questions and Hierarchical Answer Decoders. The hierarchical prompting module pre-aligns hierarchical text prompts with image features to guide the model in focusing on specific image regions according to question types, while the hierarchical decoder performs separate predictions for questions at different levels to improve accuracy across granularities. The framework also incorporates a cross-attention fusion module where images serve as queries and text as key-value pairs. Experiments on the Rad-Restruct benchmark demonstrate that the HiCA-VQA framework better outperforms existing state-of-the-art methods in answering hierarchical fine-grained questions. This study provides an effective pathway for hierarchical visual question answering systems, advancing medical image understanding.
Protein Large Language Models: A Comprehensive Survey
Feb 21, 2025Abstract:Protein-specific large language models (Protein LLMs) are revolutionizing protein science by enabling more efficient protein structure prediction, function annotation, and design. While existing surveys focus on specific aspects or applications, this work provides the first comprehensive overview of Protein LLMs, covering their architectures, training datasets, evaluation metrics, and diverse applications. Through a systematic analysis of over 100 articles, we propose a structured taxonomy of state-of-the-art Protein LLMs, analyze how they leverage large-scale protein sequence data for improved accuracy, and explore their potential in advancing protein engineering and biomedical research. Additionally, we discuss key challenges and future directions, positioning Protein LLMs as essential tools for scientific discovery in protein science. Resources are maintained at https://github.com/Yijia-Xiao/Protein-LLM-Survey.
DuoGuard: A Two-Player RL-Driven Framework for Multilingual LLM Guardrails
Feb 07, 2025



Abstract:The rapid advancement of large language models (LLMs) has increased the need for guardrail models to ensure responsible use, particularly in detecting unsafe and illegal content. While substantial safety data exist in English, multilingual guardrail modeling remains underexplored due to the scarcity of open-source safety data in other languages. To address this gap, we propose a novel two-player Reinforcement Learning (RL) framework, where a generator and a guardrail model co-evolve adversarially to produce high-quality synthetic data for multilingual guardrail training. We theoretically formalize this interaction as a two-player game, proving convergence to a Nash equilibrium. Empirical evaluations show that our model \ours outperforms state-of-the-art models, achieving nearly 10% improvement over LlamaGuard3 (8B) on English benchmarks while being 4.5x faster at inference with a significantly smaller model (0.5B). We achieve substantial advancements in multilingual safety tasks, particularly in addressing the imbalance for lower-resource languages in a collected real dataset. Ablation studies emphasize the critical role of synthetic data generation in bridging the imbalance in open-source data between English and other languages. These findings establish a scalable and efficient approach to synthetic data generation, paving the way for improved multilingual guardrail models to enhance LLM safety. Code, model, and data will be open-sourced at https://github.com/yihedeng9/DuoGuard.
MetaScientist: A Human-AI Synergistic Framework for Automated Mechanical Metamaterial Design
Dec 20, 2024



Abstract:The discovery of novel mechanical metamaterials, whose properties are dominated by their engineered structures rather than chemical composition, is a knowledge-intensive and resource-demanding process. To accelerate the design of novel metamaterials, we present MetaScientist, a human-in-the-loop system that integrates advanced AI capabilities with expert oversight with two primary phases: (1) hypothesis generation, where the system performs complex reasoning to generate novel and scientifically sound hypotheses, supported with domain-specific foundation models and inductive biases retrieved from existing literature; (2) 3D structure synthesis, where a 3D structure is synthesized with a novel 3D diffusion model based on the textual hypothesis and refined it with a LLM-based refinement model to achieve better structure properties. At each phase, domain experts iteratively validate the system outputs, and provide feedback and supplementary materials to ensure the alignment of the outputs with scientific principles and human preferences. Through extensive evaluation from human scientists, MetaScientist is able to deliver novel and valid mechanical metamaterial designs that have the potential to be highly impactful in the metamaterial field.
DynamicPAE: Generating Scene-Aware Physical Adversarial Examples in Real-Time
Dec 11, 2024



Abstract:Physical adversarial examples (PAEs) are regarded as "whistle-blowers" of real-world risks in deep-learning applications. However, current PAE generation studies show limited adaptive attacking ability to diverse and varying scenes. The key challenges in generating dynamic PAEs are exploring their patterns under noisy gradient feedback and adapting the attack to agnostic scenario natures. To address the problems, we present DynamicPAE, the first generative framework that enables scene-aware real-time physical attacks beyond static attacks. Specifically, to train the dynamic PAE generator under noisy gradient feedback, we introduce the residual-driven sample trajectory guidance technique, which redefines the training task to break the limited feedback information restriction that leads to the degeneracy problem. Intuitively, it allows the gradient feedback to be passed to the generator through a low-noise auxiliary task, thereby guiding the optimization away from degenerate solutions and facilitating a more comprehensive and stable exploration of feasible PAEs. To adapt the generator to agnostic scenario natures, we introduce the context-aligned scene expectation simulation process, consisting of the conditional-uncertainty-aligned data module and the skewness-aligned objective re-weighting module. The former enhances robustness in the context of incomplete observation by employing a conditional probabilistic model for domain randomization, while the latter facilitates consistent stealth control across different attack targets by automatically reweighting losses based on the skewness indicator. Extensive digital and physical evaluations demonstrate the superior attack performance of DynamicPAE, attaining a 1.95 $\times$ boost (65.55% average AP drop under attack) on representative object detectors (e.g., Yolo-v8) over state-of-the-art static PAE generating methods.
Uncertainty-Aware Reward-Free Exploration with General Function Approximation
Jun 24, 2024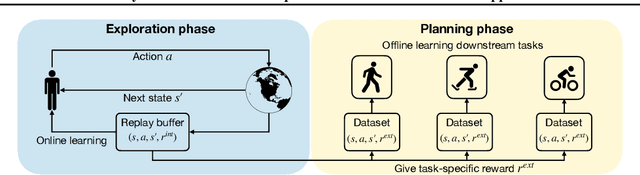
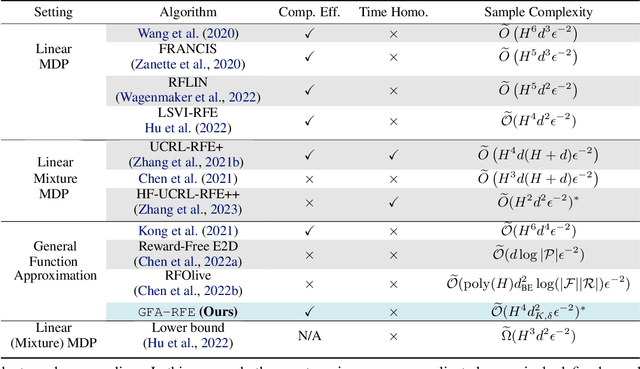

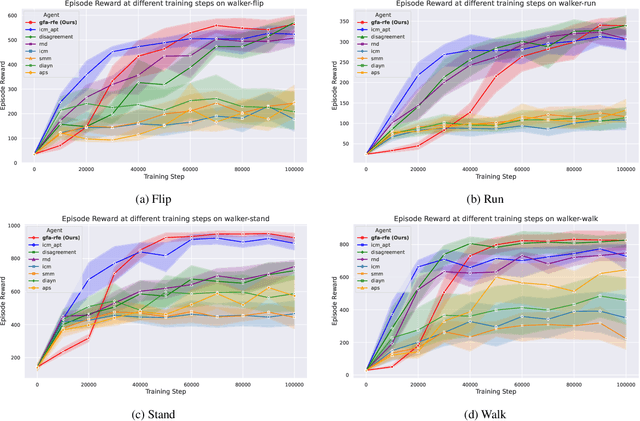
Abstract:Mastering multiple tasks through exploration and learning in an environment poses a significant challenge in reinforcement learning (RL). Unsupervised RL has been introduced to address this challenge by training policies with intrinsic rewards rather than extrinsic rewards. However, current intrinsic reward designs and unsupervised RL algorithms often overlook the heterogeneous nature of collected samples, thereby diminishing their sample efficiency. To overcome this limitation, in this paper, we propose a reward-free RL algorithm called \alg. The key idea behind our algorithm is an uncertainty-aware intrinsic reward for exploring the environment and an uncertainty-weighted learning process to handle heterogeneous uncertainty in different samples. Theoretically, we show that in order to find an $\epsilon$-optimal policy, GFA-RFE needs to collect $\tilde{O} (H^2 \log N_{\mathcal F} (\epsilon) \mathrm{dim} (\mathcal F) / \epsilon^2 )$ number of episodes, where $\mathcal F$ is the value function class with covering number $N_{\mathcal F} (\epsilon)$ and generalized eluder dimension $\mathrm{dim} (\mathcal F)$. Such a result outperforms all existing reward-free RL algorithms. We further implement and evaluate GFA-RFE across various domains and tasks in the DeepMind Control Suite. Experiment results show that GFA-RFE outperforms or is comparable to the performance of state-of-the-art unsupervised RL algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge