Scaling Agents via Continual Pre-training

Large language models (LLMs) have evolved into agentic systems capable of autonomous tool use and multi-step reasoning for complex problem-solving. However, post-training approaches building upon general-purpose foundation models consistently underperform in agentic tasks, particularly in open-source implementations. We identify the root cause: the absence of robust agentic foundation models forces models during post-training to simultaneously learn diverse agentic behaviors while aligning them to expert demonstrations, thereby creating fundamental optimization tensions. To this end, we are the first to propose incorporating Agentic Continual Pre-training (Agentic CPT) into the deep research agents training pipeline to build powerful agentic foundational models. Based on this approach, we develop a deep research agent model named AgentFounder. We evaluate our AgentFounder-30B on 10 benchmarks and achieve state-of-the-art performance while retains strong tool-use ability, notably 39.9% on BrowseComp-en, 43.3% on BrowseComp-zh, and 31.5% Pass@1 on HLE.

WebSailor-V2: Bridging the Chasm to Proprietary Agents via Synthetic Data and Scalable Reinforcement Learning

Transcending human cognitive limitations represents a critical frontier in LLM training. Proprietary agentic systems like DeepResearch have demonstrated superhuman capabilities on extremely complex information-seeking benchmarks such as BrowseComp, a feat previously unattainable. We posit that their success hinges on a sophisticated reasoning pattern absent in open-source models: the ability to systematically reduce extreme uncertainty when navigating vast information landscapes. Based on this insight, we introduce WebSailor, a complete post-training methodology designed to instill this crucial capability. Our approach involves generating novel, high-uncertainty tasks through structured sampling and information obfuscation, RFT cold start, and an efficient agentic RL training algorithm, Duplicating Sampling Policy Optimization (DUPO). With this integrated pipeline, WebSailor significantly outperforms all open-source agents in complex information-seeking tasks, matching proprietary agents' performance and closing the capability gap.

ReSum: Unlocking Long-Horizon Search Intelligence via Context Summarization

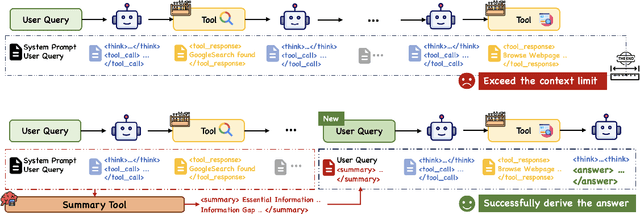
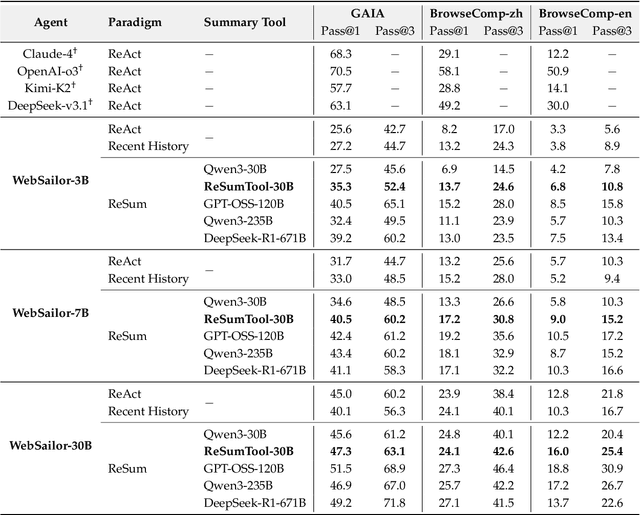
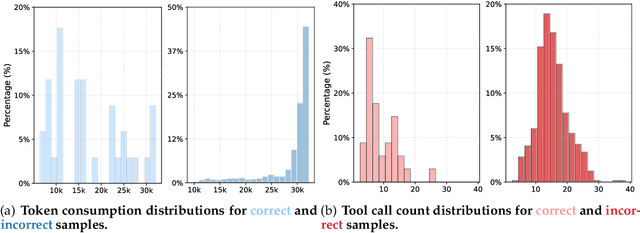
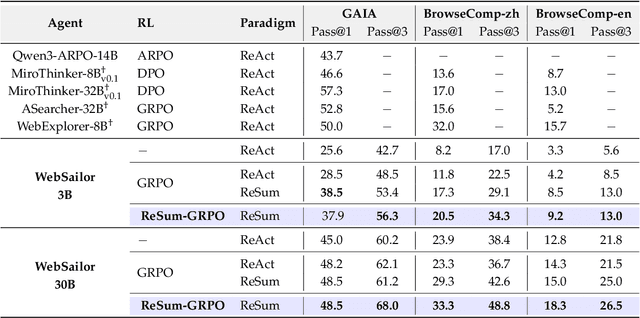
Large Language Model (LLM)-based web agents demonstrate strong performance on knowledge-intensive tasks but are hindered by context window limitations in paradigms like ReAct. Complex queries involving multiple entities, intertwined relationships, and high uncertainty demand extensive search cycles that rapidly exhaust context budgets before reaching complete solutions. To overcome this challenge, we introduce ReSum, a novel paradigm that enables indefinite exploration through periodic context summarization. ReSum converts growing interaction histories into compact reasoning states, maintaining awareness of prior discoveries while bypassing context constraints. For paradigm adaptation, we propose ReSum-GRPO, integrating GRPO with segmented trajectory training and advantage broadcasting to familiarize agents with summary-conditioned reasoning. Extensive experiments on web agents of varying scales across three benchmarks demonstrate that ReSum delivers an average absolute improvement of 4.5\% over ReAct, with further gains of up to 8.2\% following ReSum-GRPO training. Notably, with only 1K training samples, our WebResummer-30B (a ReSum-GRPO-trained version of WebSailor-30B) achieves 33.3\% Pass@1 on BrowseComp-zh and 18.3\% on BrowseComp-en, surpassing existing open-source web agents.

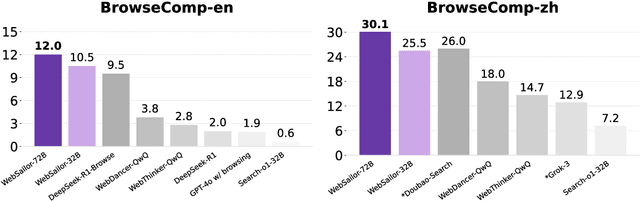
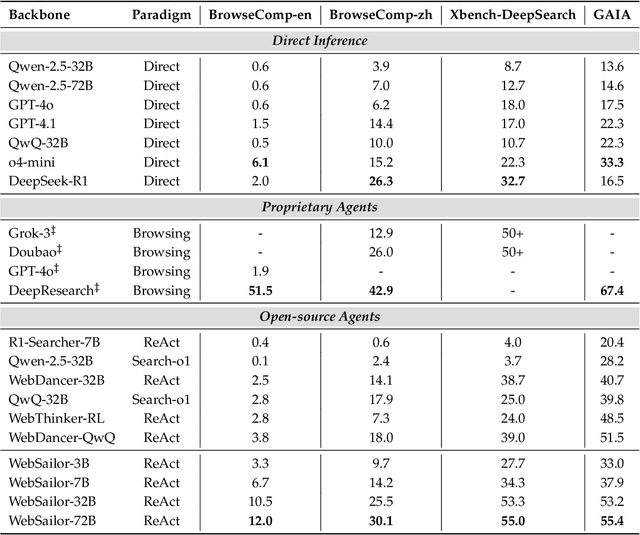
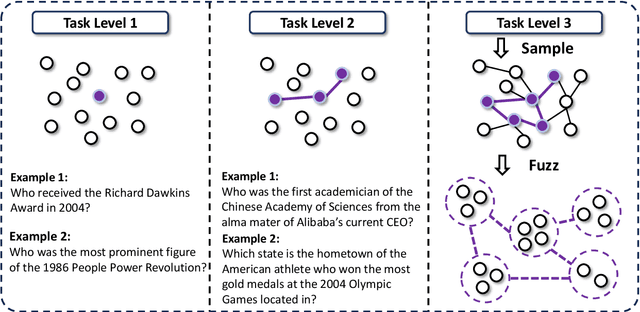
WebSailor: Navigating Super-human Reasoning for Web Agent

Transcending human cognitive limitations represents a critical frontier in LLM training. Proprietary agentic systems like DeepResearch have demonstrated superhuman capabilities on extremely complex information-seeking benchmarks such as BrowseComp, a feat previously unattainable. We posit that their success hinges on a sophisticated reasoning pattern absent in open-source models: the ability to systematically reduce extreme uncertainty when navigating vast information landscapes. Based on this insight, we introduce WebSailor, a complete post-training methodology designed to instill this crucial capability. Our approach involves generating novel, high-uncertainty tasks through structured sampling and information obfuscation, RFT cold start, and an efficient agentic RL training algorithm, Duplicating Sampling Policy Optimization (DUPO). With this integrated pipeline, WebSailor significantly outperforms all opensource agents in complex information-seeking tasks, matching proprietary agents' performance and closing the capability gap.

Scalable Complexity Control Facilitates Reasoning Ability of LLMs

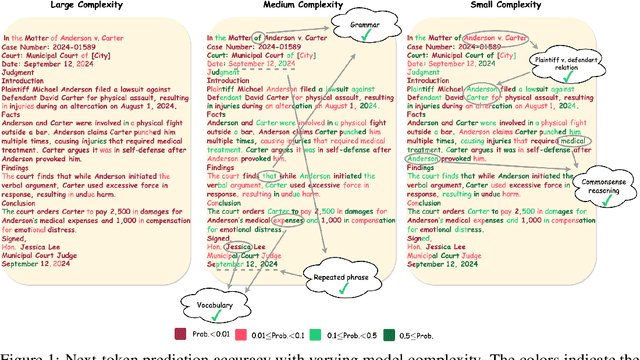
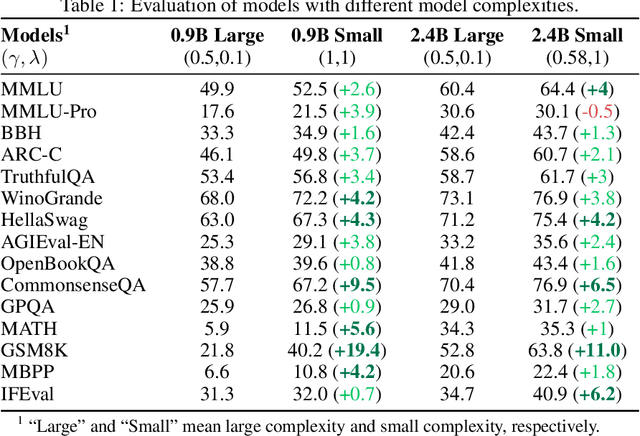
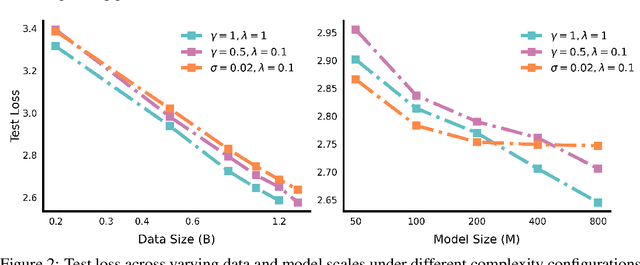
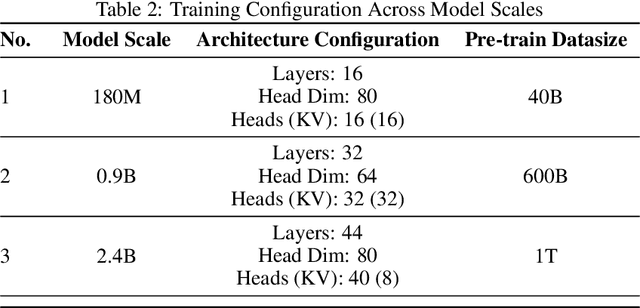
The reasoning ability of large language models (LLMs) has been rapidly advancing in recent years, attracting interest in more fundamental approaches that can reliably enhance their generalizability. This work demonstrates that model complexity control, conveniently implementable by adjusting the initialization rate and weight decay coefficient, improves the scaling law of LLMs consistently over varying model sizes and data sizes. This gain is further illustrated by comparing the benchmark performance of 2.4B models pretrained on 1T tokens with different complexity hyperparameters. Instead of fixing the initialization std, we found that a constant initialization rate (the exponent of std) enables the scaling law to descend faster in both model and data sizes. These results indicate that complexity control is a promising direction for the continual advancement of LLMs.

An Analysis for Reasoning Bias of Language Models with Small Initialization

Transformer-based Large Language Models (LLMs) have revolutionized Natural Language Processing by demonstrating exceptional performance across diverse tasks. This study investigates the impact of the parameter initialization scale on the training behavior and task preferences of LLMs. We discover that smaller initialization scales encourage models to favor reasoning tasks, whereas larger initialization scales lead to a preference for memorization tasks. We validate this reasoning bias via real datasets and meticulously designed anchor functions. Further analysis of initial training dynamics suggests that specific model components, particularly the embedding space and self-attention mechanisms, play pivotal roles in shaping these learning biases. We provide a theoretical framework from the perspective of model training dynamics to explain these phenomena. Additionally, experiments on real-world language tasks corroborate our theoretical insights. This work enhances our understanding of how initialization strategies influence LLM performance on reasoning tasks and offers valuable guidelines for training models.

Reasoning Bias of Next Token Prediction Training

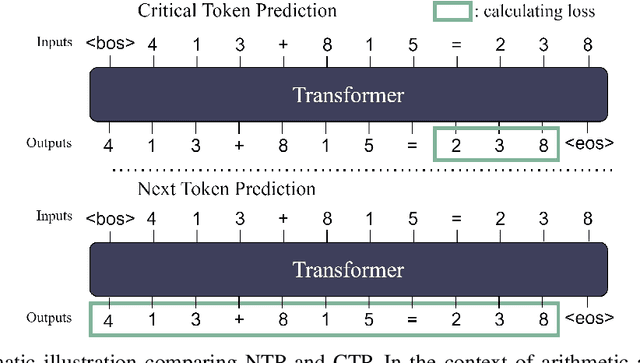
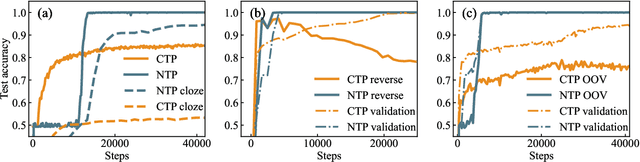
Since the inception of Large Language Models (LLMs), the quest to efficiently train them for superior reasoning capabilities has been a pivotal challenge. The dominant training paradigm for LLMs is based on next token prediction (NTP). Alternative methodologies, called Critical Token Prediction (CTP), focused exclusively on specific critical tokens (such as the answer in Q\&A dataset), aiming to reduce the overfitting of extraneous information and noise. Contrary to initial assumptions, our research reveals that despite NTP's exposure to noise during training, it surpasses CTP in reasoning ability. We attribute this counterintuitive outcome to the regularizing influence of noise on the training dynamics. Our empirical analysis shows that NTP-trained models exhibit enhanced generalization and robustness across various benchmark reasoning datasets, demonstrating greater resilience to perturbations and achieving flatter loss minima. These findings illuminate that NTP is instrumental in fostering reasoning abilities during pretraining, whereas CTP is more effective for finetuning, thereby enriching our comprehension of optimal training strategies in LLM development.

Complexity Control Facilitates Reasoning-Based Compositional Generalization in Transformers

Transformers have demonstrated impressive capabilities across various tasks, yet their performance on compositional problems remains a subject of debate. In this study, we investigate the internal mechanisms underlying Transformers' behavior in compositional tasks. We find that complexity control strategies significantly influence whether the model learns primitive-level rules that generalize out-of-distribution (reasoning-based solutions) or relies solely on memorized mappings (memory-based solutions). By applying masking strategies to the model's information circuits and employing multiple complexity metrics, we reveal distinct internal working mechanisms associated with different solution types. Further analysis reveals that reasoning-based solutions exhibit a lower complexity bias, which aligns with the well-studied neuron condensation phenomenon. This lower complexity bias is hypothesized to be the key factor enabling these solutions to learn reasoning rules. We validate these conclusions across multiple real-world datasets, including image generation and natural language processing tasks, confirming the broad applicability of our findings.

Local Linear Recovery Guarantee of Deep Neural Networks at Overparameterization

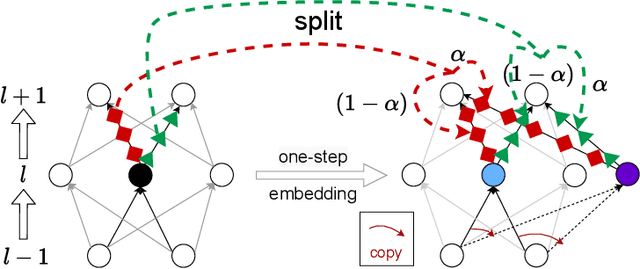
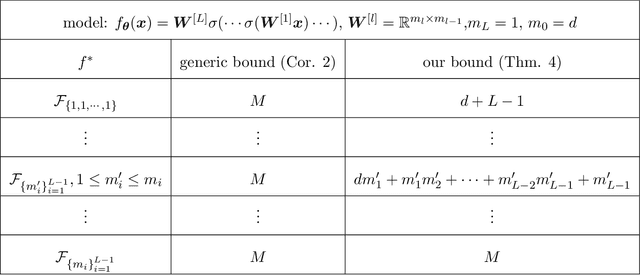
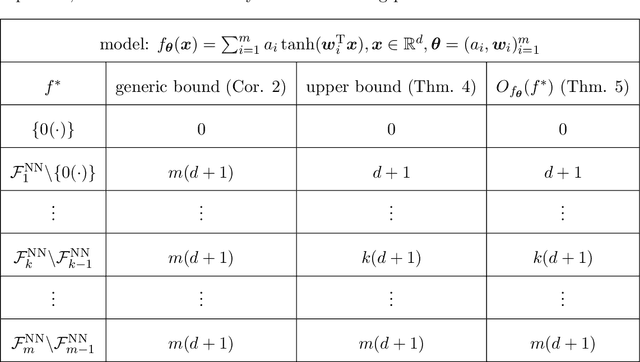
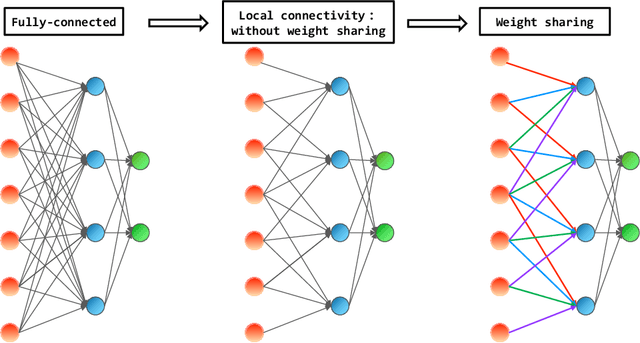
Determining whether deep neural network (DNN) models can reliably recover target functions at overparameterization is a critical yet complex issue in the theory of deep learning. To advance understanding in this area, we introduce a concept we term "local linear recovery" (LLR), a weaker form of target function recovery that renders the problem more amenable to theoretical analysis. In the sense of LLR, we prove that functions expressible by narrower DNNs are guaranteed to be recoverable from fewer samples than model parameters. Specifically, we establish upper limits on the optimistic sample sizes, defined as the smallest sample size necessary to guarantee LLR, for functions in the space of a given DNN. Furthermore, we prove that these upper bounds are achieved in the case of two-layer tanh neural networks. Our research lays a solid groundwork for future investigations into the recovery capabilities of DNNs in overparameterized scenarios.

Towards Understanding How Transformer Perform Multi-step Reasoning with Matching Operation

Large language models have consistently struggled with complex reasoning tasks, such as mathematical problem-solving. Investigating the internal reasoning mechanisms of these models can help us design better model architectures and training strategies, ultimately enhancing their reasoning capabilities. In this study, we examine the matching mechanism employed by Transformer for multi-step reasoning on a constructed dataset. We investigate factors that influence the model's matching mechanism and discover that small initialization and post-LayerNorm can facilitate the formation of the matching mechanism, thereby enhancing the model's reasoning ability. Moreover, we propose a method to improve the model's reasoning capability by adding orthogonal noise. Finally, we investigate the parallel reasoning mechanism of Transformers and propose a conjecture on the upper bound of the model's reasoning ability based on this phenomenon. These insights contribute to a deeper understanding of the reasoning processes in large language models and guide designing more effective reasoning architectures and training strategies.