Adaptive Preconditioners Trigger Loss Spikes in Adam

Loss spikes emerge commonly during training across neural networks of varying architectures and scales when using the Adam optimizer. In this work, we investigate the underlying mechanism responsible for Adam spikes. While previous explanations attribute these phenomena to the lower-loss-as-sharper characteristics of the loss landscape, our analysis reveals that Adam's adaptive preconditioners themselves can trigger spikes. Specifically, we identify a critical regime where squared gradients become substantially smaller than the second-order moment estimates, causing the latter to undergo a $\beta_2$-exponential decay and to respond sluggishly to current gradient information. This mechanism can push the maximum eigenvalue of the preconditioned Hessian beyond the classical stability threshold $2/\eta$ for a sustained period, inducing instability. This instability further leads to an alignment between the gradient and the maximum eigendirection, and a loss spike occurs precisely when the gradient-directional curvature exceeds $2/\eta$. We verify this mechanism through extensive experiments on fully connected networks, convolutional networks, and Transformer architectures.

Scalable Complexity Control Facilitates Reasoning Ability of LLMs

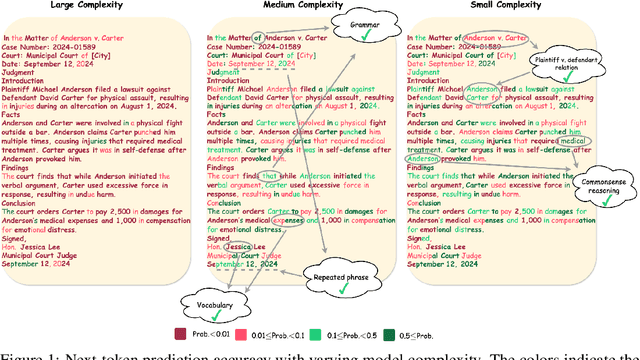
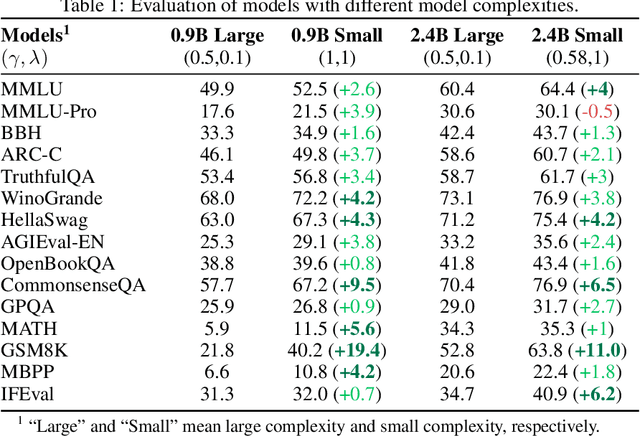
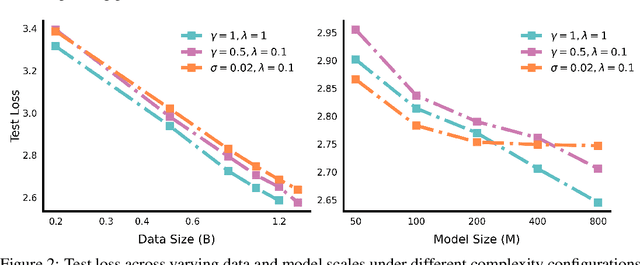
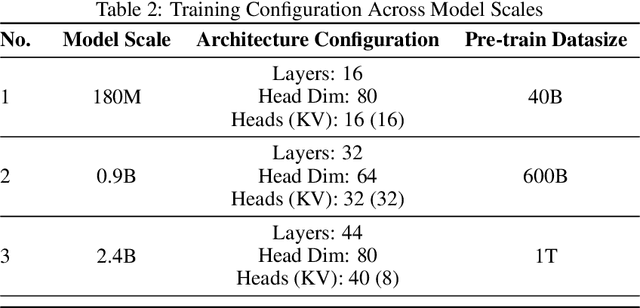
The reasoning ability of large language models (LLMs) has been rapidly advancing in recent years, attracting interest in more fundamental approaches that can reliably enhance their generalizability. This work demonstrates that model complexity control, conveniently implementable by adjusting the initialization rate and weight decay coefficient, improves the scaling law of LLMs consistently over varying model sizes and data sizes. This gain is further illustrated by comparing the benchmark performance of 2.4B models pretrained on 1T tokens with different complexity hyperparameters. Instead of fixing the initialization std, we found that a constant initialization rate (the exponent of std) enables the scaling law to descend faster in both model and data sizes. These results indicate that complexity control is a promising direction for the continual advancement of LLMs.

MemOS: An Operating System for Memory-Augmented Generation (MAG) in Large Language Models

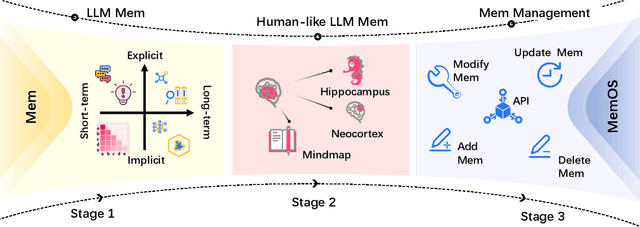
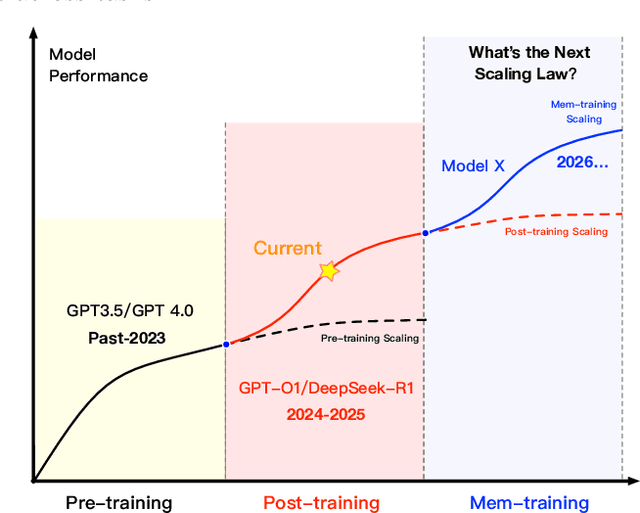
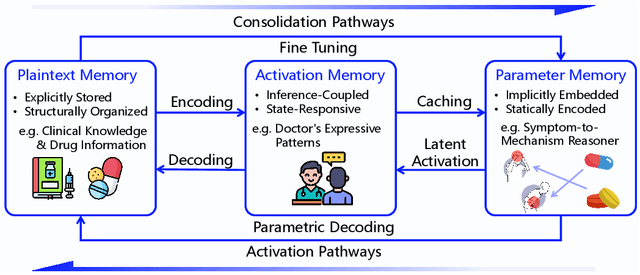
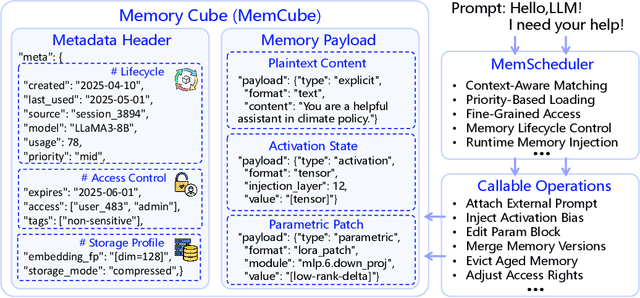
Large Language Models (LLMs) have emerged as foundational infrastructure in the pursuit of Artificial General Intelligence (AGI). Despite their remarkable capabilities in language perception and generation, current LLMs fundamentally lack a unified and structured architecture for handling memory. They primarily rely on parametric memory (knowledge encoded in model weights) and ephemeral activation memory (context-limited runtime states). While emerging methods like Retrieval-Augmented Generation (RAG) incorporate plaintext memory, they lack lifecycle management and multi-modal integration, limiting their capacity for long-term knowledge evolution. To address this, we introduce MemOS, a memory operating system designed for LLMs that, for the first time, elevates memory to a first-class operational resource. It builds unified mechanisms for representation, organization, and governance across three core memory types: parametric, activation, and plaintext. At its core is the MemCube, a standardized memory abstraction that enables tracking, fusion, and migration of heterogeneous memory, while offering structured, traceable access across tasks and contexts. MemOS establishes a memory-centric execution framework with strong controllability, adaptability, and evolvability. It fills a critical gap in current LLM infrastructure and lays the groundwork for continual adaptation, personalized intelligence, and cross-platform coordination in next-generation intelligent systems.

An overview of condensation phenomenon in deep learning

In this paper, we provide an overview of a common phenomenon, condensation, observed during the nonlinear training of neural networks: During the nonlinear training of neural networks, neurons in the same layer tend to condense into groups with similar outputs. Empirical observations suggest that the number of condensed clusters of neurons in the same layer typically increases monotonically as training progresses. Neural networks with small weight initializations or Dropout optimization can facilitate this condensation process. We also examine the underlying mechanisms of condensation from the perspectives of training dynamics and the structure of the loss landscape. The condensation phenomenon offers valuable insights into the generalization abilities of neural networks and correlates to stronger reasoning abilities in transformer-based language models.

An Analysis for Reasoning Bias of Language Models with Small Initialization

Transformer-based Large Language Models (LLMs) have revolutionized Natural Language Processing by demonstrating exceptional performance across diverse tasks. This study investigates the impact of the parameter initialization scale on the training behavior and task preferences of LLMs. We discover that smaller initialization scales encourage models to favor reasoning tasks, whereas larger initialization scales lead to a preference for memorization tasks. We validate this reasoning bias via real datasets and meticulously designed anchor functions. Further analysis of initial training dynamics suggests that specific model components, particularly the embedding space and self-attention mechanisms, play pivotal roles in shaping these learning biases. We provide a theoretical framework from the perspective of model training dynamics to explain these phenomena. Additionally, experiments on real-world language tasks corroborate our theoretical insights. This work enhances our understanding of how initialization strategies influence LLM performance on reasoning tasks and offers valuable guidelines for training models.

Reasoning Bias of Next Token Prediction Training

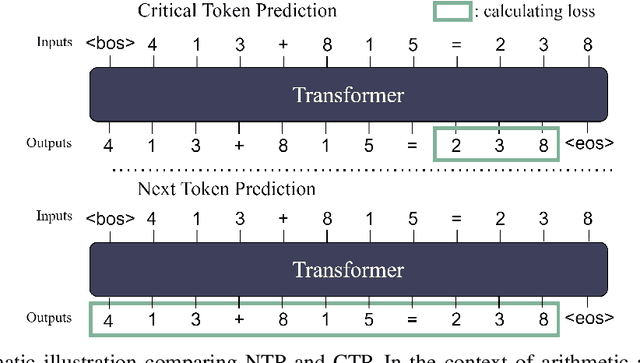
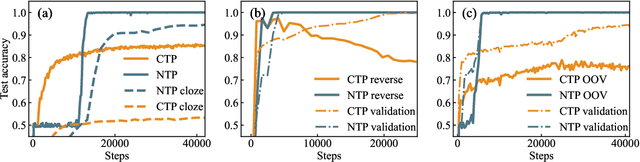
Since the inception of Large Language Models (LLMs), the quest to efficiently train them for superior reasoning capabilities has been a pivotal challenge. The dominant training paradigm for LLMs is based on next token prediction (NTP). Alternative methodologies, called Critical Token Prediction (CTP), focused exclusively on specific critical tokens (such as the answer in Q\&A dataset), aiming to reduce the overfitting of extraneous information and noise. Contrary to initial assumptions, our research reveals that despite NTP's exposure to noise during training, it surpasses CTP in reasoning ability. We attribute this counterintuitive outcome to the regularizing influence of noise on the training dynamics. Our empirical analysis shows that NTP-trained models exhibit enhanced generalization and robustness across various benchmark reasoning datasets, demonstrating greater resilience to perturbations and achieving flatter loss minima. These findings illuminate that NTP is instrumental in fostering reasoning abilities during pretraining, whereas CTP is more effective for finetuning, thereby enriching our comprehension of optimal training strategies in LLM development.

Complexity Control Facilitates Reasoning-Based Compositional Generalization in Transformers

Transformers have demonstrated impressive capabilities across various tasks, yet their performance on compositional problems remains a subject of debate. In this study, we investigate the internal mechanisms underlying Transformers' behavior in compositional tasks. We find that complexity control strategies significantly influence whether the model learns primitive-level rules that generalize out-of-distribution (reasoning-based solutions) or relies solely on memorized mappings (memory-based solutions). By applying masking strategies to the model's information circuits and employing multiple complexity metrics, we reveal distinct internal working mechanisms associated with different solution types. Further analysis reveals that reasoning-based solutions exhibit a lower complexity bias, which aligns with the well-studied neuron condensation phenomenon. This lower complexity bias is hypothesized to be the key factor enabling these solutions to learn reasoning rules. We validate these conclusions across multiple real-world datasets, including image generation and natural language processing tasks, confirming the broad applicability of our findings.

A rationale from frequency perspective for grokking in training neural network

Grokking is the phenomenon where neural networks NNs initially fit the training data and later generalize to the test data during training. In this paper, we empirically provide a frequency perspective to explain the emergence of this phenomenon in NNs. The core insight is that the networks initially learn the less salient frequency components present in the test data. We observe this phenomenon across both synthetic and real datasets, offering a novel viewpoint for elucidating the grokking phenomenon by characterizing it through the lens of frequency dynamics during the training process. Our empirical frequency-based analysis sheds new light on understanding the grokking phenomenon and its underlying mechanisms.

Towards Understanding How Transformer Perform Multi-step Reasoning with Matching Operation

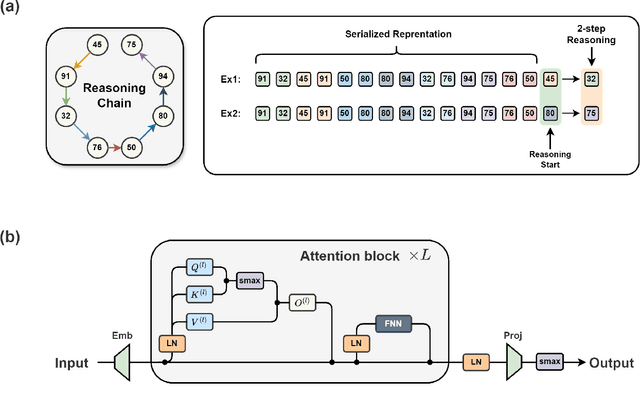
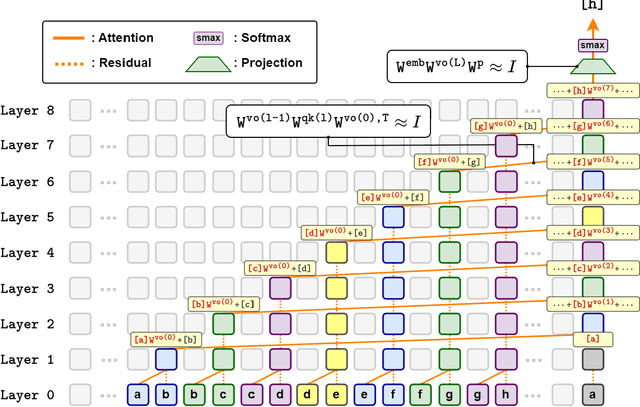
Large language models have consistently struggled with complex reasoning tasks, such as mathematical problem-solving. Investigating the internal reasoning mechanisms of these models can help us design better model architectures and training strategies, ultimately enhancing their reasoning capabilities. In this study, we examine the matching mechanism employed by Transformer for multi-step reasoning on a constructed dataset. We investigate factors that influence the model's matching mechanism and discover that small initialization and post-LayerNorm can facilitate the formation of the matching mechanism, thereby enhancing the model's reasoning ability. Moreover, we propose a method to improve the model's reasoning capability by adding orthogonal noise. Finally, we investigate the parallel reasoning mechanism of Transformers and propose a conjecture on the upper bound of the model's reasoning ability based on this phenomenon. These insights contribute to a deeper understanding of the reasoning processes in large language models and guide designing more effective reasoning architectures and training strategies.

Initialization is Critical to Whether Transformers Fit Composite Functions by Inference or Memorizing

Transformers have shown impressive capabilities across various tasks, but their performance on compositional problems remains a topic of debate. In this work, we investigate the mechanisms of how transformers behave on unseen compositional tasks using anchor functions. We discover that the parameter initialization scale plays a critical role in determining whether the model learns inferential solutions, which capture the underlying compositional primitives, or symmetric solutions, which simply memorize mappings without understanding the compositional structure. By analyzing the information flow and vector representations within the model, we reveal the distinct mechanisms underlying these solution types. We further find that inferential solutions exhibit low complexity bias, which we hypothesize is a key factor enabling them to learn individual mappings for single anchors. Building upon our understanding of these mechanisms, we can predict the learning behavior of models with different initialization scales when faced with data of varying inferential complexity. Our findings provide valuable insights into the role of initialization scale in shaping the type of solution learned by transformers and their ability to learn and generalize compositional functions.