ICH-SCNet: Intracerebral Hemorrhage Segmentation and Prognosis Classification Network Using CLIP-guided SAM mechanism

Intracerebral hemorrhage (ICH) is the most fatal subtype of stroke and is characterized by a high incidence of disability. Accurate segmentation of the ICH region and prognosis prediction are critically important for developing and refining treatment plans for post-ICH patients. However, existing approaches address these two tasks independently and predominantly focus on imaging data alone, thereby neglecting the intrinsic correlation between the tasks and modalities. This paper introduces a multi-task network, ICH-SCNet, designed for both ICH segmentation and prognosis classification. Specifically, we integrate a SAM-CLIP cross-modal interaction mechanism that combines medical text and segmentation auxiliary information with neuroimaging data to enhance cross-modal feature recognition. Additionally, we develop an effective feature fusion module and a multi-task loss function to improve performance further. Extensive experiments on an ICH dataset reveal that our approach surpasses other state-of-the-art methods. It excels in the overall performance of classification tasks and outperforms competing models in all segmentation task metrics.

Exact Conversion of In-Context Learning to Model Weights in Linearized-Attention Transformers

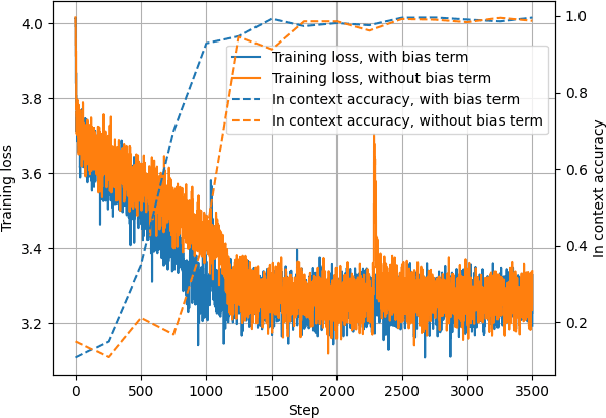
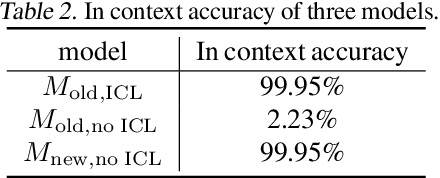
In-Context Learning (ICL) has been a powerful emergent property of large language models that has attracted increasing attention in recent years. In contrast to regular gradient-based learning, ICL is highly interpretable and does not require parameter updates. In this paper, we show that, for linearized transformer networks, ICL can be made explicit and permanent through the inclusion of bias terms. We mathematically demonstrate the equivalence between a model with ICL demonstration prompts and the same model with the additional bias terms. Our algorithm (ICLCA) allows for exact conversion in an inexpensive manner. Existing methods are not exact and require expensive parameter updates. We demonstrate the efficacy of our approach through experiments that show the exact incorporation of ICL tokens into a linear transformer. We further suggest how our method can be adapted to achieve cheap approximate conversion of ICL tokens, even in regular transformer networks that are not linearized. Our experiments on GPT-2 show that, even though the conversion is only approximate, the model still gains valuable context from the included bias terms.

Towards Understanding How Transformer Perform Multi-step Reasoning with Matching Operation

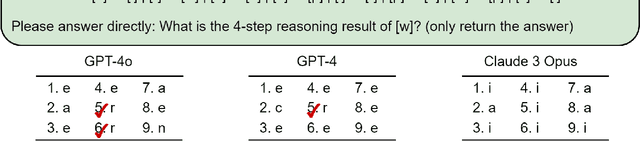
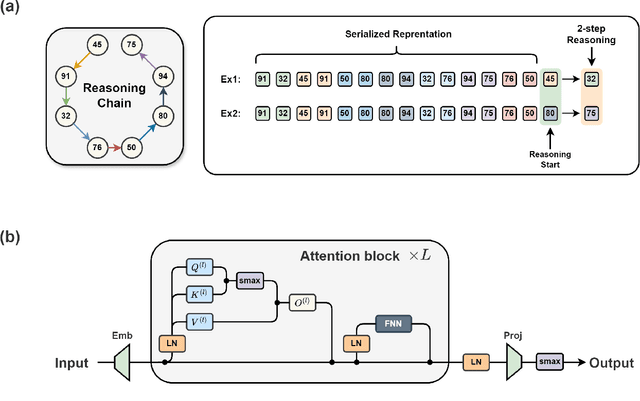
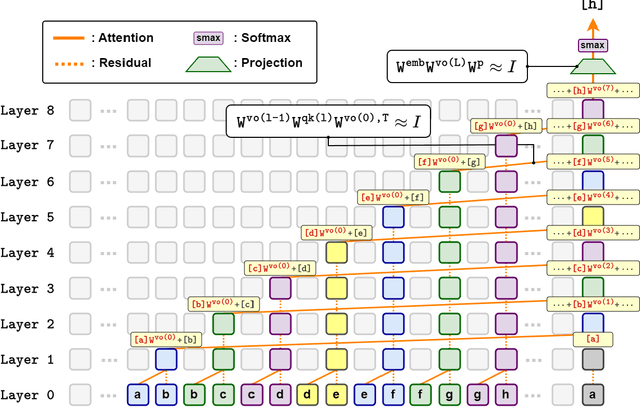
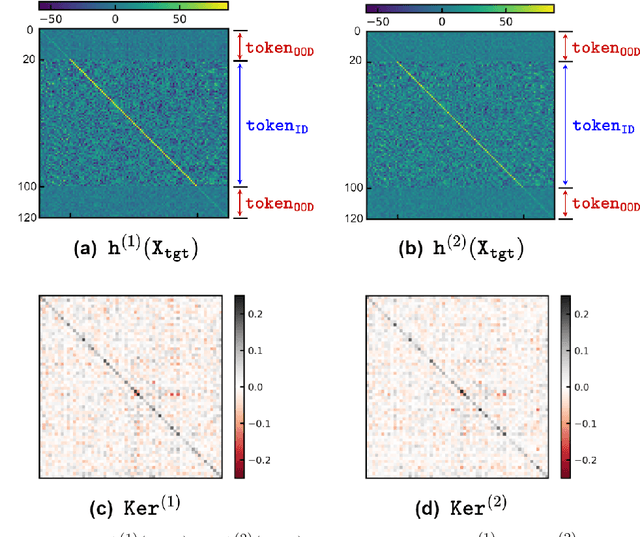
Large language models have consistently struggled with complex reasoning tasks, such as mathematical problem-solving. Investigating the internal reasoning mechanisms of these models can help us design better model architectures and training strategies, ultimately enhancing their reasoning capabilities. In this study, we examine the matching mechanism employed by Transformer for multi-step reasoning on a constructed dataset. We investigate factors that influence the model's matching mechanism and discover that small initialization and post-LayerNorm can facilitate the formation of the matching mechanism, thereby enhancing the model's reasoning ability. Moreover, we propose a method to improve the model's reasoning capability by adding orthogonal noise. Finally, we investigate the parallel reasoning mechanism of Transformers and propose a conjecture on the upper bound of the model's reasoning ability based on this phenomenon. These insights contribute to a deeper understanding of the reasoning processes in large language models and guide designing more effective reasoning architectures and training strategies.

Characterizing the Spectrum of the NTK via a Power Series Expansion

Under mild conditions on the network initialization we derive a power series expansion for the Neural Tangent Kernel (NTK) of arbitrarily deep feedforward networks in the infinite width limit. We provide expressions for the coefficients of this power series which depend on both the Hermite coefficients of the activation function as well as the depth of the network. We observe faster decay of the Hermite coefficients leads to faster decay in the NTK coefficients. Using this series, first we relate the effective rank of the NTK to the effective rank of the input-data Gram. Second, for data drawn uniformly on the sphere we derive an explicit formula for the eigenvalues of the NTK, which shows faster decay in the NTK coefficients implies a faster decay in its spectrum. From this we recover existing results on eigenvalue asymptotics for ReLU networks and comment on how the activation function influences the RKHS. Finally, for generic data and activation functions with sufficiently fast Hermite coefficient decay, we derive an asymptotic upper bound on the spectrum of the NTK.

Learning curves for Gaussian process regression with power-law priors and targets

We study the power-law asymptotics of learning curves for Gaussian process regression (GPR). When the eigenspectrum of the prior decays with rate $\alpha$ and the eigenexpansion coefficients of the target function decay with rate $\beta$, we show that the generalization error behaves as $\tilde O(n^{\max\{\frac{1}{\alpha}-1, \frac{1-2\beta}{\alpha}\}})$ with high probability over the draw of $n$ input samples. Under similar assumptions, we show that the generalization error of kernel ridge regression (KRR) has the same asymptotics. Infinitely wide neural networks can be related to KRR with respect to the neural tangent kernel (NTK), which in several cases is known to have a power-law spectrum. Hence our methods can be applied to study the generalization error of infinitely wide neural networks. We present toy experiments demonstrating the theory.

Implicit bias of gradient descent for mean squared error regression with wide neural networks

We investigate gradient descent training of wide neural networks and the corresponding implicit bias in function space. Focusing on 1D regression, we show that the solution of training a width-$n$ shallow ReLU network is within $n^{- 1/2}$ of the function which fits the training data and whose difference from initialization has smallest 2-norm of the second derivative weighted by $1/\zeta$. The curvature penalty function $1/\zeta$ is expressed in terms of the probability distribution that is utilized to initialize the network parameters, and we compute it explicitly for various common initialization procedures. For instance, asymmetric initialization with a uniform distribution yields a constant curvature penalty, and thence the solution function is the natural cubic spline interpolation of the training data. The statement generalizes to the training trajectories, which in turn are captured by trajectories of spatially adaptive smoothing splines with decreasing regularization strength.