Bounds for the smallest eigenvalue of the NTK for arbitrary spherical data of arbitrary dimension

Bounds on the smallest eigenvalue of the neural tangent kernel (NTK) are a key ingredient in the analysis of neural network optimization and memorization. However, existing results require distributional assumptions on the data and are limited to a high-dimensional setting, where the input dimension $d_0$ scales at least logarithmically in the number of samples $n$. In this work we remove both of these requirements and instead provide bounds in terms of a measure of the collinearity of the data: notably these bounds hold with high probability even when $d_0$ is held constant versus $n$. We prove our results through a novel application of the hemisphere transform.

Benign overfitting in leaky ReLU networks with moderate input dimension

The problem of benign overfitting asks whether it is possible for a model to perfectly fit noisy training data and still generalize well. We study benign overfitting in two-layer leaky ReLU networks trained with the hinge loss on a binary classification task. We consider input data which can be decomposed into the sum of a common signal and a random noise component, which lie on subspaces orthogonal to one another. We characterize conditions on the signal to noise ratio (SNR) of the model parameters giving rise to benign versus non-benign, or harmful, overfitting: in particular, if the SNR is high then benign overfitting occurs, conversely if the SNR is low then harmful overfitting occurs. We attribute both benign and non-benign overfitting to an approximate margin maximization property and show that leaky ReLU networks trained on hinge loss with Gradient Descent (GD) satisfy this property. In contrast to prior work we do not require near orthogonality conditions on the training data: notably, for input dimension $d$ and training sample size $n$, while prior work shows asymptotically optimal error when $d = \Omega(n^2 \log n)$, here we require only $d = \Omega\left(n \log \frac{1}{\epsilon}\right)$ to obtain error within $\epsilon$ of optimal.

Training shallow ReLU networks on noisy data using hinge loss: when do we overfit and is it benign?

We study benign overfitting in two-layer ReLU networks trained using gradient descent and hinge loss on noisy data for binary classification. In particular, we consider linearly separable data for which a relatively small proportion of labels are corrupted or flipped. We identify conditions on the margin of the clean data that give rise to three distinct training outcomes: benign overfitting, in which zero loss is achieved and with high probability test data is classified correctly; overfitting, in which zero loss is achieved but test data is misclassified with probability lower bounded by a constant; and non-overfitting, in which clean points, but not corrupt points, achieve zero loss and again with high probability test data is classified correctly. Our analysis provides a fine-grained description of the dynamics of neurons throughout training and reveals two distinct phases: in the first phase clean points achieve close to zero loss, in the second phase clean points oscillate on the boundary of zero loss while corrupt points either converge towards zero loss or are eventually zeroed by the network. We prove these results using a combinatorial approach that involves bounding the number of clean versus corrupt updates across these phases of training.

Mildly Overparameterized ReLU Networks Have a Favorable Loss Landscape

We study the loss landscape of two-layer mildly overparameterized ReLU neural networks on a generic finite input dataset for the squared error loss. Our approach involves bounding the dimension of the sets of local and global minima using the rank of the Jacobian of the parameterization map. Using results on random binary matrices, we show most activation patterns correspond to parameter regions with no bad differentiable local minima. Furthermore, for one-dimensional input data, we show most activation regions realizable by the network contain a high dimensional set of global minima and no bad local minima. We experimentally confirm these results by finding a phase transition from most regions having full rank to many regions having deficient rank depending on the amount of overparameterization.

Characterizing the Spectrum of the NTK via a Power Series Expansion

Under mild conditions on the network initialization we derive a power series expansion for the Neural Tangent Kernel (NTK) of arbitrarily deep feedforward networks in the infinite width limit. We provide expressions for the coefficients of this power series which depend on both the Hermite coefficients of the activation function as well as the depth of the network. We observe faster decay of the Hermite coefficients leads to faster decay in the NTK coefficients. Using this series, first we relate the effective rank of the NTK to the effective rank of the input-data Gram. Second, for data drawn uniformly on the sphere we derive an explicit formula for the eigenvalues of the NTK, which shows faster decay in the NTK coefficients implies a faster decay in its spectrum. From this we recover existing results on eigenvalue asymptotics for ReLU networks and comment on how the activation function influences the RKHS. Finally, for generic data and activation functions with sufficiently fast Hermite coefficient decay, we derive an asymptotic upper bound on the spectrum of the NTK.

Activation function design for deep networks: linearity and effective initialisation

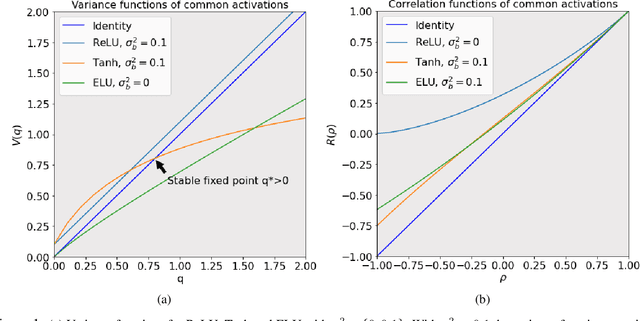
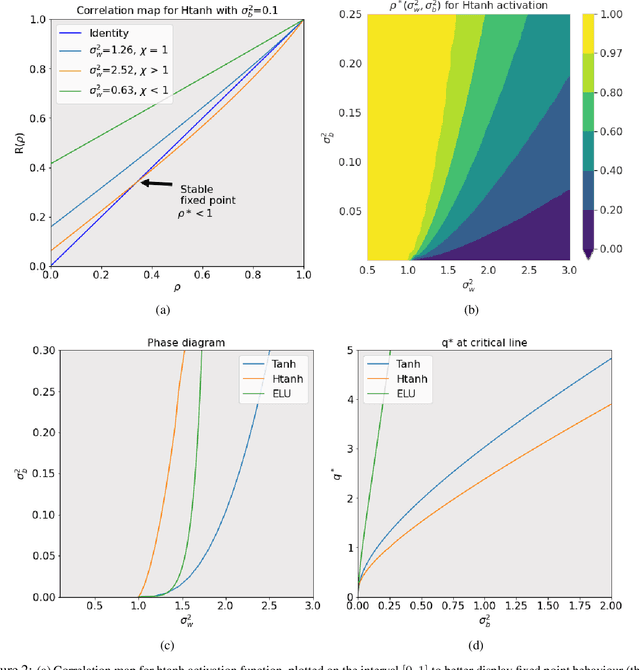
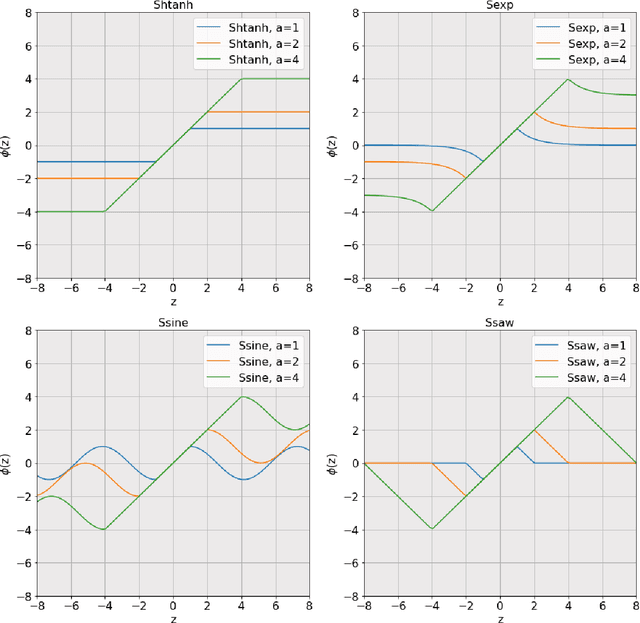
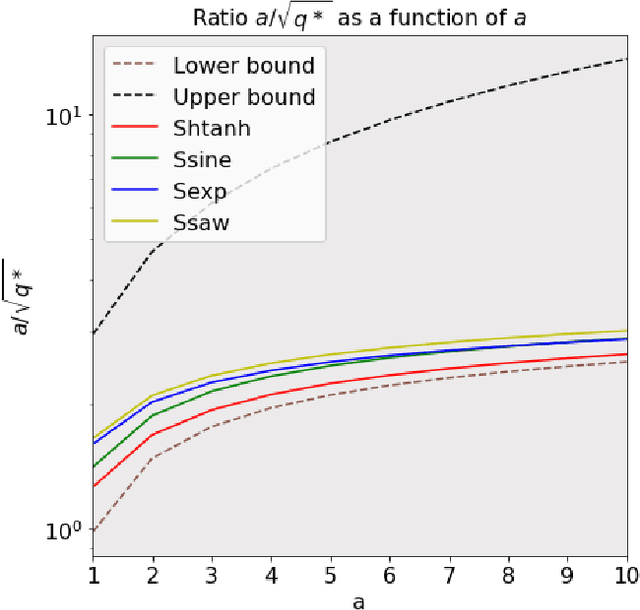
The activation function deployed in a deep neural network has great influence on the performance of the network at initialisation, which in turn has implications for training. In this paper we study how to avoid two problems at initialisation identified in prior works: rapid convergence of pairwise input correlations, and vanishing and exploding gradients. We prove that both these problems can be avoided by choosing an activation function possessing a sufficiently large linear region around the origin, relative to the bias variance $\sigma_b^2$ of the network's random initialisation. We demonstrate empirically that using such activation functions leads to tangible benefits in practice, both in terms test and training accuracy as well as training time. Furthermore, we observe that the shape of the nonlinear activation outside the linear region appears to have a relatively limited impact on training. Finally, our results also allow us to train networks in a new hyperparameter regime, with a much larger bias variance than has previously been possible.

The Permuted Striped Block Model and its Factorization -- Algorithms with Recovery Guarantees

We introduce a novel class of matrices which are defined by the factorization $\textbf{Y} :=\textbf{A}\textbf{X}$, where $\textbf{A}$ is an $m \times n$ wide sparse binary matrix with a fixed number $d$ nonzeros per column and $\textbf{X}$ is an $n \times N$ sparse real matrix whose columns have at most $k$ nonzeros and are $\textit{dissociated}$. Matrices defined by this factorization can be expressed as a sum of $n$ rank one sparse matrices, whose nonzero entries, under the appropriate permutations, form striped blocks - we therefore refer to them as Permuted Striped Block (PSB) matrices. We define the $\textit{PSB data model}$ as a particular distribution over this class of matrices, motivated by its implications for community detection, provable binary dictionary learning with real valued sparse coding, and blind combinatorial compressed sensing. For data matrices drawn from the PSB data model, we provide computationally efficient factorization algorithms which recover the generating factors with high probability from as few as $N =O\left(\frac{n}{k}\log^2(n)\right)$ data vectors, where $k$, $m$ and $n$ scale proportionally. Notably, these algorithms achieve optimal sample complexity up to logarithmic factors.

Vision-and-Dialog Navigation

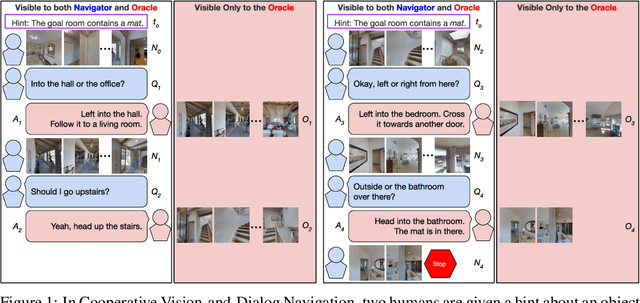
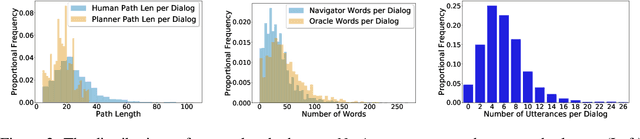
Robots navigating in human environments should use language to ask for assistance and be able to understand human responses. To study this challenge, we introduce Cooperative Vision-and-Dialog Navigation, a dataset of over 2k embodied, human-human dialogs situated in simulated, photorealistic home environments. The Navigator asks questions to their partner, the Oracle, who has privileged access to the best next steps the Navigator should take according to a shortest path planner. To train agents that search an environment for a goal location, we define the Navigation from Dialog History task. An agent, given a target object and a dialog history between humans cooperating to find that object, must infer navigation actions towards the goal in unexplored environments. We establish an initial, multi-modal sequence-to-sequence model and demonstrate that looking farther back in the dialog history improves performance. Sourcecode and a live interface demo can be found at https://github.com/mmurray/cvdn

Towards an understanding of CNNs: analysing the recovery of activation pathways via Deep Convolutional Sparse Coding

Deep Convolutional Sparse Coding (D-CSC) is a framework reminiscent of deep convolutional neural networks (DCNNs), but by omitting the learning of the dictionaries one can more transparently analyse the role of the activation function and its ability to recover activation paths through the layers. Papyan, Romano, and Elad conducted an analysis of such an architecture, demonstrated the relationship with DCNNs and proved conditions under which the D-CSC is guaranteed to recover specific activation paths. A technical innovation of their work highlights that one can view the efficacy of the ReLU nonlinear activation function of a DCNN through a new variant of the tensor's sparsity, referred to as stripe-sparsity. Using this they proved that representations with an activation density proportional to the ambient dimension of the data are recoverable. We extend their uniform guarantees to a modified model and prove that with high probability the true activation is typically possible to recover for a greater density of activations per layer. Our extension follows from incorporating the prior work on one step thresholding by Schnass and Vandergheynst.