Mind the Gap: a Spectral Analysis of Rank Collapse and Signal Propagation in Transformers

Attention layers are the core component of transformers, the current state-of-the-art neural network architecture. However, \softmaxx-based attention puts transformers' trainability at risk. Even \textit{at initialisation}, the propagation of signals and gradients through the random network can be pathological, resulting in known issues such as (i) vanishing/exploding gradients and (ii) \textit{rank collapse}, i.e. when all tokens converge to a single representation \textit{with depth}. This paper examines signal propagation in \textit{attention-only} transformers from a random matrix perspective, illuminating the origin of such issues, as well as unveiling a new phenomenon -- (iii) rank collapse \textit{in width}. Modelling \softmaxx-based attention at initialisation with Random Markov matrices, our theoretical analysis reveals that a \textit{spectral gap} between the two largest singular values of the attention matrix causes (iii), which, in turn, exacerbates (i) and (ii). Building on this insight, we propose a novel, yet simple, practical solution to resolve rank collapse in width by removing the spectral gap. Moreover, we validate our findings and discuss the training benefits of the proposed fix through experiments that also motivate a revision of some of the default parameter scaling. Our attention model accurately describes the standard key-query attention in a single-layer transformer, making this work a significant first step towards a better understanding of the initialisation dynamics in the multi-layer case.

Deep Neural Network Initialization with Sparsity Inducing Activations

Inducing and leveraging sparse activations during training and inference is a promising avenue for improving the computational efficiency of deep networks, which is increasingly important as network sizes continue to grow and their application becomes more widespread. Here we use the large width Gaussian process limit to analyze the behaviour, at random initialization, of nonlinear activations that induce sparsity in the hidden outputs. A previously unreported form of training instability is proven for arguably two of the most natural candidates for hidden layer sparsification; those being a shifted ReLU ($\phi(x)=\max(0, x-\tau)$ for $\tau\ge 0$) and soft thresholding ($\phi(x)=0$ for $|x|\le\tau$ and $x-\text{sign}(x)\tau$ for $|x|>\tau$). We show that this instability is overcome by clipping the nonlinear activation magnitude, at a level prescribed by the shape of the associated Gaussian process variance map. Numerical experiments verify the theory and show that the proposed magnitude clipped sparsifying activations can be trained with training and test fractional sparsity as high as 85\% while retaining close to full accuracy.

Beyond IID weights: sparse and low-rank deep Neural Networks are also Gaussian Processes

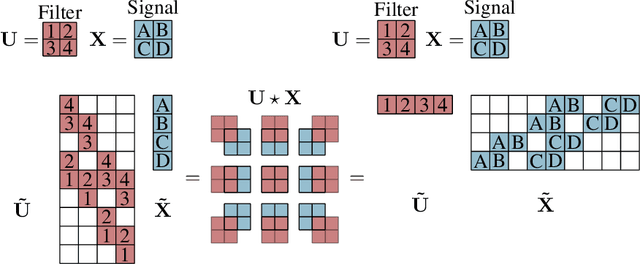
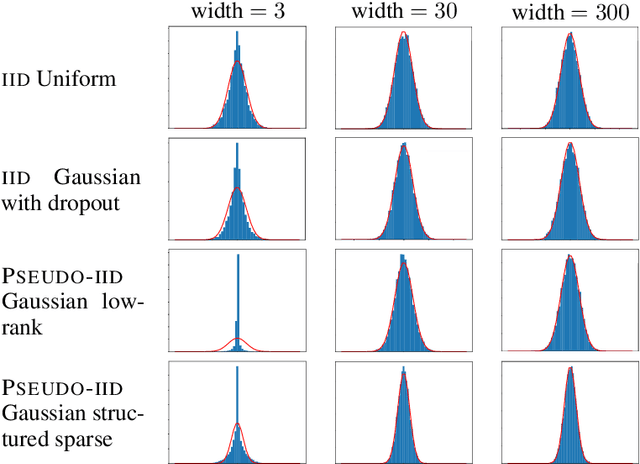
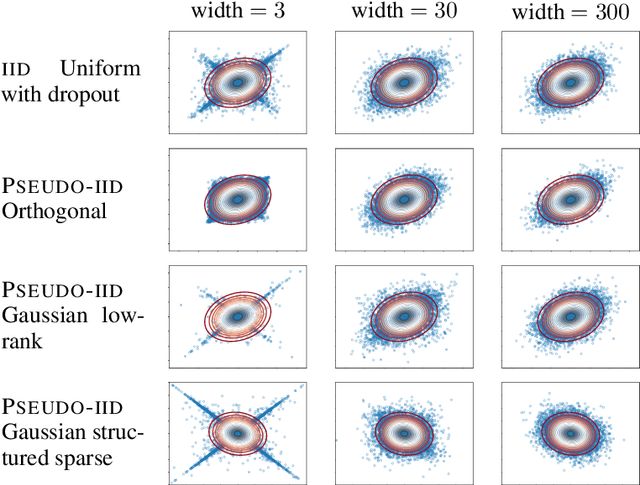
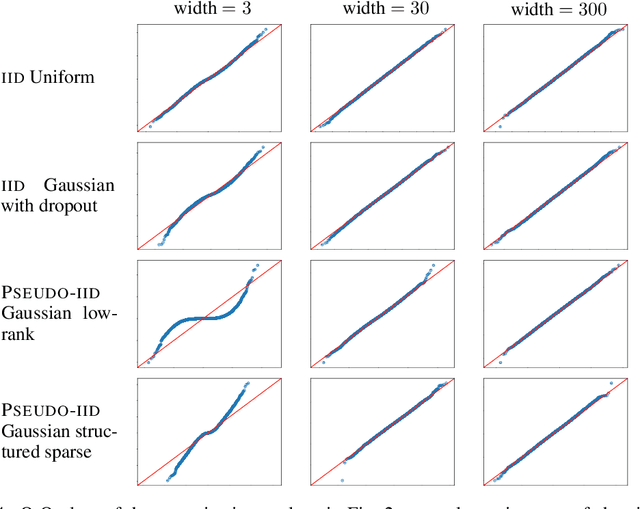
The infinitely wide neural network has been proven a useful and manageable mathematical model that enables the understanding of many phenomena appearing in deep learning. One example is the convergence of random deep networks to Gaussian processes that allows a rigorous analysis of the way the choice of activation function and network weights impacts the training dynamics. In this paper, we extend the seminal proof of Matthews et al. (2018) to a larger class of initial weight distributions (which we call PSEUDO-IID), including the established cases of IID and orthogonal weights, as well as the emerging low-rank and structured sparse settings celebrated for their computational speed-up benefits. We show that fully-connected and convolutional networks initialized with PSEUDO-IID distributions are all effectively equivalent up to their variance. Using our results, one can identify the Edge-of-Chaos for a broader class of neural networks and tune them at criticality in order to enhance their training.

Dynamic Sparse No Training: Training-Free Fine-tuning for Sparse LLMs

The ever-increasing large language models (LLMs), though opening a potential path for the upcoming artificial general intelligence, sadly drops a daunting obstacle on the way towards their on-device deployment. As one of the most well-established pre-LLMs approaches in reducing model complexity, network pruning appears to lag behind in the era of LLMs, due mostly to its costly fine-tuning (or re-training) necessity under the massive volumes of model parameter and training data. To close this industry-academia gap, we introduce Dynamic Sparse No Training (DSnoT), a training-free fine-tuning approach that slightly updates sparse LLMs without the expensive backpropagation and any weight updates. Inspired by the Dynamic Sparse Training, DSnoT minimizes the reconstruction error between the dense and sparse LLMs, in the fashion of performing iterative weight pruning-and-growing on top of sparse LLMs. To accomplish this purpose, DSnoT particularly takes into account the anticipated reduction in reconstruction error for pruning and growing, as well as the variance w.r.t. different input data for growing each weight. This practice can be executed efficiently in linear time since its obviates the need of backpropagation for fine-tuning LLMs. Extensive experiments on LLaMA-V1/V2, Vicuna, and OPT across various benchmarks demonstrate the effectiveness of DSnoT in enhancing the performance of sparse LLMs, especially at high sparsity levels. For instance, DSnoT is able to outperform the state-of-the-art Wanda by 26.79 perplexity at 70% sparsity with LLaMA-7B. Our paper offers fresh insights into how to fine-tune sparse LLMs in an efficient training-free manner and open new venues to scale the great potential of sparsity to LLMs. Codes are available at https://github.com/zyxxmu/DSnoT.

On the Initialisation of Wide Low-Rank Feedforward Neural Networks

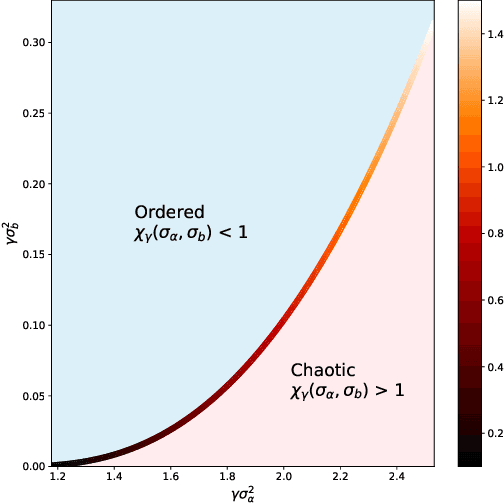
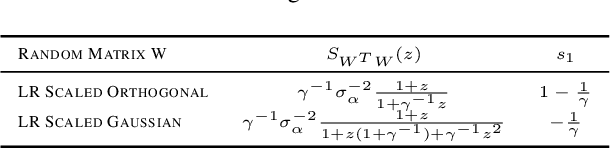
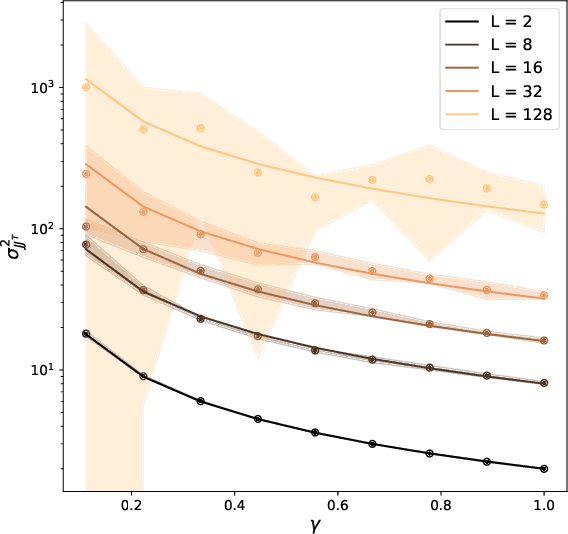
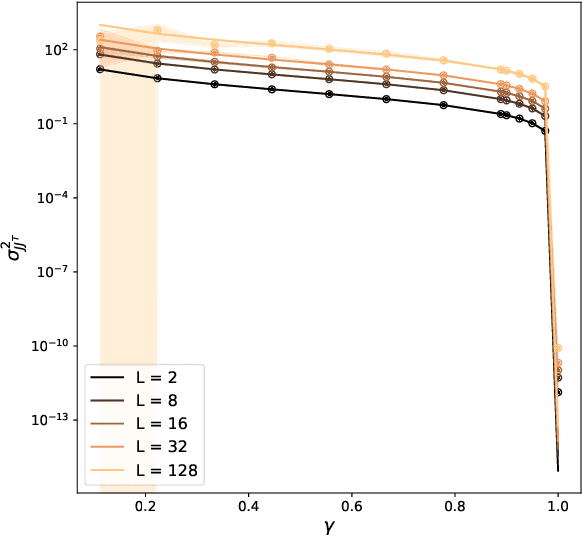
The edge-of-chaos dynamics of wide randomly initialized low-rank feedforward networks are analyzed. Formulae for the optimal weight and bias variances are extended from the full-rank to low-rank setting and are shown to follow from multiplicative scaling. The principle second order effect, the variance of the input-output Jacobian, is derived and shown to increase as the rank to width ratio decreases. These results inform practitioners how to randomly initialize feedforward networks with a reduced number of learnable parameters while in the same ambient dimension, allowing reductions in the computational cost and memory constraints of the associated network.

Optimal Approximation Complexity of High-Dimensional Functions with Neural Networks

We investigate properties of neural networks that use both ReLU and $x^2$ as activation functions and build upon previous results to show that both analytic functions and functions in Sobolev spaces can be approximated by such networks of constant depth to arbitrary accuracy, demonstrating optimal order approximation rates across all nonlinear approximators, including standard ReLU networks. We then show how to leverage low local dimensionality in some contexts to overcome the curse of dimensionality, obtaining approximation rates that are optimal for unknown lower-dimensional subspaces.

Improved Projection Learning for Lower Dimensional Feature Maps

The requirement to repeatedly move large feature maps off- and on-chip during inference with convolutional neural networks (CNNs) imposes high costs in terms of both energy and time. In this work we explore an improved method for compressing all feature maps of pre-trained CNNs to below a specified limit. This is done by means of learned projections trained via end-to-end finetuning, which can then be folded and fused into the pre-trained network. We also introduce a new `ceiling compression' framework in which evaluate such techniques in view of the future goal of performing inference fully on-chip.

Tuning-free multi-coil compressed sensing MRI with Parallel Variable Density Approximate Message Passing

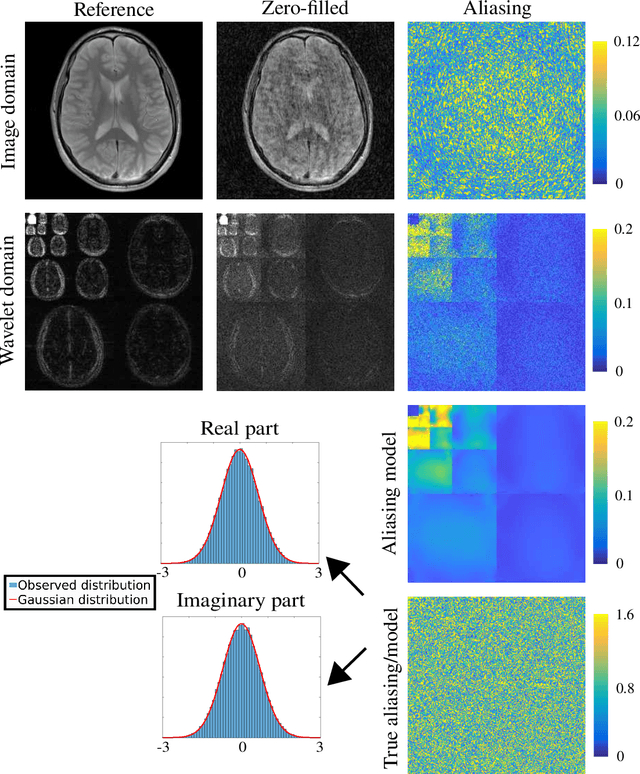
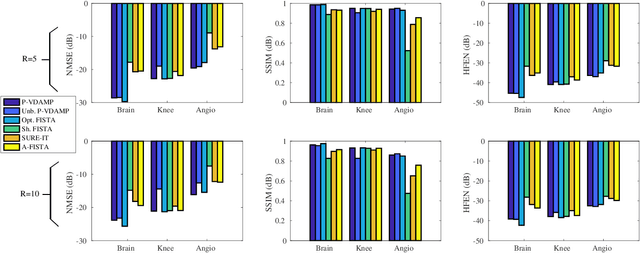
Purpose: To develop a tuning-free method for multi-coil compressed sensing MRI that performs competitively with algorithms with an optimally tuned sparse parameter. Theory: The Parallel Variable Density Approximate Message Passing (P-VDAMP) algorithm is proposed. For Bernoulli random variable density sampling, P-VDAMP obeys a "state evolution", where the intermediate per-iteration image estimate is distributed according to the ground truth corrupted by a Gaussian vector with approximately known covariance. State evolution is leveraged to automatically tune sparse parameters on-the-fly with Stein's Unbiased Risk Estimate (SURE). Methods: P-VDAMP is evaluated on brain, knee and angiogram datasets at acceleration factors 5 and 10 and compared with four variants of the Fast Iterative Shrinkage-Thresholding algorithm (FISTA), including two tuning-free variants from the literature. Results: The proposed method is found to have a similar reconstruction quality and time to convergence as FISTA with an optimally tuned sparse weighting. Conclusions: P-VDAMP is an efficient, robust and principled method for on-the-fly parameter tuning that is competitive with optimally tuned FISTA and offers substantial robustness and reconstruction quality improvements over competing tuning-free methods.

Activation function design for deep networks: linearity and effective initialisation

The activation function deployed in a deep neural network has great influence on the performance of the network at initialisation, which in turn has implications for training. In this paper we study how to avoid two problems at initialisation identified in prior works: rapid convergence of pairwise input correlations, and vanishing and exploding gradients. We prove that both these problems can be avoided by choosing an activation function possessing a sufficiently large linear region around the origin, relative to the bias variance $\sigma_b^2$ of the network's random initialisation. We demonstrate empirically that using such activation functions leads to tangible benefits in practice, both in terms test and training accuracy as well as training time. Furthermore, we observe that the shape of the nonlinear activation outside the linear region appears to have a relatively limited impact on training. Finally, our results also allow us to train networks in a new hyperparameter regime, with a much larger bias variance than has previously been possible.

Dense for the Price of Sparse: Improved Performance of Sparsely Initialized Networks via a Subspace Offset

That neural networks may be pruned to high sparsities and retain high accuracy is well established. Recent research efforts focus on pruning immediately after initialization so as to allow the computational savings afforded by sparsity to extend to the training process. In this work, we introduce a new `DCT plus Sparse' layer architecture, which maintains information propagation and trainability even with as little as 0.01% trainable kernel parameters remaining. We show that standard training of networks built with these layers, and pruned at initialization, achieves state-of-the-art accuracy for extreme sparsities on a variety of benchmark network architectures and datasets. Moreover, these results are achieved using only simple heuristics to determine the locations of the trainable parameters in the network, and thus without having to initially store or compute with the full, unpruned network, as is required by competing prune-at-initialization algorithms. Switching from standard sparse layers to DCT plus Sparse layers does not increase the storage footprint of a network and incurs only a small additional computational overhead.