Mind the Gap: a Spectral Analysis of Rank Collapse and Signal Propagation in Transformers

Attention layers are the core component of transformers, the current state-of-the-art neural network architecture. However, \softmaxx-based attention puts transformers' trainability at risk. Even \textit{at initialisation}, the propagation of signals and gradients through the random network can be pathological, resulting in known issues such as (i) vanishing/exploding gradients and (ii) \textit{rank collapse}, i.e. when all tokens converge to a single representation \textit{with depth}. This paper examines signal propagation in \textit{attention-only} transformers from a random matrix perspective, illuminating the origin of such issues, as well as unveiling a new phenomenon -- (iii) rank collapse \textit{in width}. Modelling \softmaxx-based attention at initialisation with Random Markov matrices, our theoretical analysis reveals that a \textit{spectral gap} between the two largest singular values of the attention matrix causes (iii), which, in turn, exacerbates (i) and (ii). Building on this insight, we propose a novel, yet simple, practical solution to resolve rank collapse in width by removing the spectral gap. Moreover, we validate our findings and discuss the training benefits of the proposed fix through experiments that also motivate a revision of some of the default parameter scaling. Our attention model accurately describes the standard key-query attention in a single-layer transformer, making this work a significant first step towards a better understanding of the initialisation dynamics in the multi-layer case.

Beyond IID weights: sparse and low-rank deep Neural Networks are also Gaussian Processes

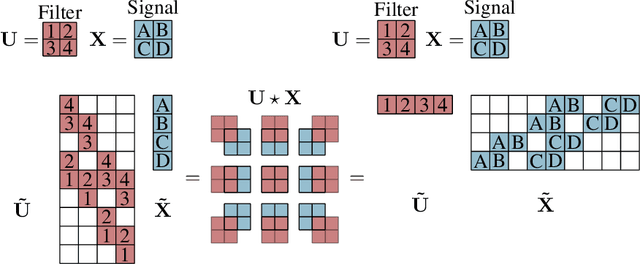
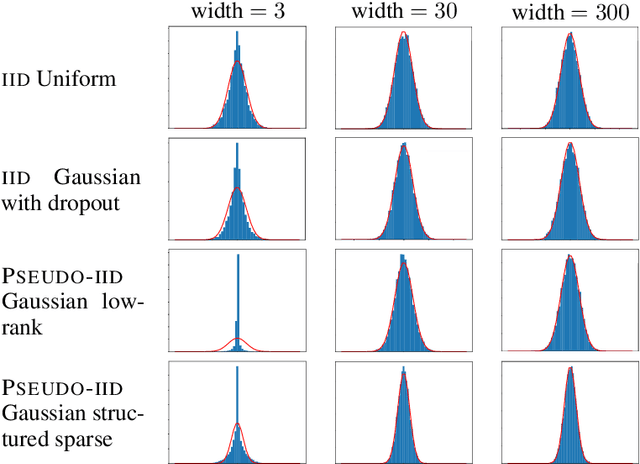
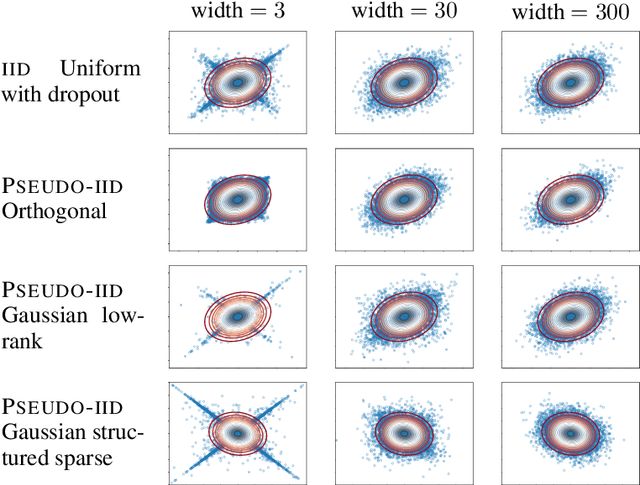
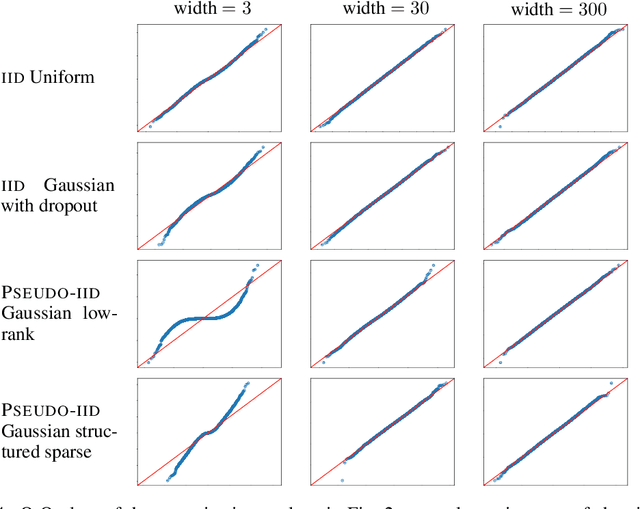
The infinitely wide neural network has been proven a useful and manageable mathematical model that enables the understanding of many phenomena appearing in deep learning. One example is the convergence of random deep networks to Gaussian processes that allows a rigorous analysis of the way the choice of activation function and network weights impacts the training dynamics. In this paper, we extend the seminal proof of Matthews et al. (2018) to a larger class of initial weight distributions (which we call PSEUDO-IID), including the established cases of IID and orthogonal weights, as well as the emerging low-rank and structured sparse settings celebrated for their computational speed-up benefits. We show that fully-connected and convolutional networks initialized with PSEUDO-IID distributions are all effectively equivalent up to their variance. Using our results, one can identify the Edge-of-Chaos for a broader class of neural networks and tune them at criticality in order to enhance their training.

Beyond Independent Measurements: General Compressed Sensing with GNN Application

We consider the problem of recovering a structured signal $\mathbf{x} \in \mathbb{R}^{n}$ from noisy linear observations $\mathbf{y} =\mathbf{M} \mathbf{x}+\mathbf{w}$. The measurement matrix is modeled as $\mathbf{M} = \mathbf{B}\mathbf{A}$, where $\mathbf{B} \in \mathbb{R}^{l \times m}$ is arbitrary and $\mathbf{A} \in \mathbb{R}^{m \times n}$ has independent sub-gaussian rows. By varying $\mathbf{B}$, and the sub-gaussian distribution of $\mathbf{A}$, this gives a family of measurement matrices which may have heavy tails, dependent rows and columns, and singular values with a large dynamic range. When the structure is given as a possibly non-convex cone $T \subset \mathbb{R}^{n}$, an approximate empirical risk minimizer is proven to be a robust estimator if the effective number of measurements is sufficient, even in the presence of a model mismatch. In classical compressed sensing with independent (sub-)gaussian measurements, one asks how many measurements are needed to recover $\mathbf{x}$? In our setting, however, the effective number of measurements depends on the properties of $\mathbf{B}$. We show that the effective rank of $\mathbf{B}$ may be used as a surrogate for the number of measurements, and if this exceeds the squared Gaussian mean width of $(T-T) \cap \mathbb{S}^{n-1}$, then accurate recovery is guaranteed. Furthermore, we examine the special case of generative priors in detail, that is when $\mathbf{x}$ lies close to $T = \mathrm{ran}(G)$ and $G: \mathbb{R}^k \rightarrow \mathbb{R}^n$ is a Generative Neural Network (GNN) with ReLU activation functions. Our work relies on a recent result in random matrix theory by Jeong, Li, Plan, and Yilmaz arXiv:2001.10631. .