CyberGFM: Graph Foundation Models for Lateral Movement Detection in Enterprise Networks

Representing networks as a graph and training a link prediction model using benign connections is an effective method of anomaly-based intrusion detection. Existing works using this technique have shown great success using temporal graph neural networks and skip-gram-based approaches on random walks. However, random walk-based approaches are unable to incorporate rich edge data, while the GNN-based approaches require large amounts of memory to train. In this work, we propose extending the original insight from random walk-based skip-grams--that random walks through a graph are analogous to sentences in a corpus--to the more modern transformer-based foundation models. Using language models that take advantage of GPU optimizations, we can quickly train a graph foundation model to predict missing tokens in random walks through a network of computers. The graph foundation model is then finetuned for link prediction and used as a network anomaly detector. This new approach allows us to combine the efficiency of random walk-based methods and the rich semantic representation of deep learning methods. This system, which we call CyberGFM, achieved state-of-the-art results on three widely used network anomaly detection datasets, delivering a up to 2$\times$ improvement in average precision. We found that CyberGFM outperforms all prior works in unsupervised link prediction for network anomaly detection, using the same number of parameters, and with equal or better efficiency than the previous best approaches.

Experience-Guided Adaptation of Inference-Time Reasoning Strategies

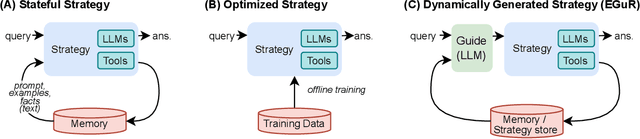
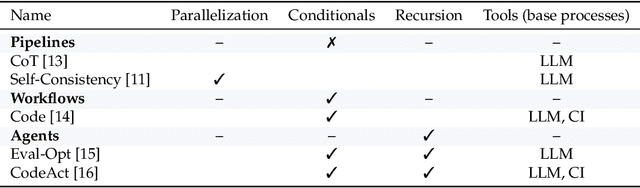
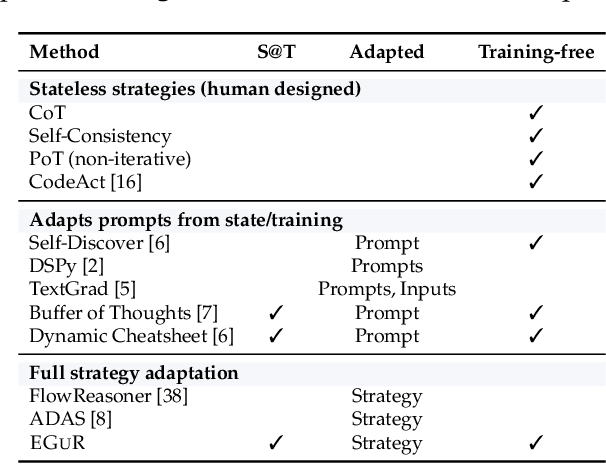
Enabling agentic AI systems to adapt their problem-solving approaches based on post-training interactions remains a fundamental challenge. While systems that update and maintain a memory at inference time have been proposed, existing designs only steer the system by modifying textual input to a language model or agent, which means that they cannot change sampling parameters, remove tools, modify system prompts, or switch between agentic and workflow paradigms. On the other hand, systems that adapt more flexibly require offline optimization and remain static once deployed. We present Experience-Guided Reasoner (EGuR), which generates tailored strategies -- complete computational procedures involving LLM calls, tools, sampling parameters, and control logic -- dynamically at inference time based on accumulated experience. We achieve this using an LLM-based meta-strategy -- a strategy that outputs strategies -- enabling adaptation of all strategy components (prompts, sampling parameters, tool configurations, and control logic). EGuR operates through two components: a Guide generates multiple candidate strategies conditioned on the current problem and structured memory of past experiences, while a Consolidator integrates execution feedback to improve future strategy generation. This produces complete, ready-to-run strategies optimized for each problem, which can be cached, retrieved, and executed as needed without wasting resources. Across five challenging benchmarks (AIME 2025, 3-SAT, and three Big Bench Extra Hard tasks), EGuR achieves up to 14% accuracy improvements over the strongest baselines while reducing computational costs by up to 111x, with both metrics improving as the system gains experience.

Automated Cyber Defense with Generalizable Graph-based Reinforcement Learning Agents

Deep reinforcement learning (RL) is emerging as a viable strategy for automated cyber defense (ACD). The traditional RL approach represents networks as a list of computers in various states of safety or threat. Unfortunately, these models are forced to overfit to specific network topologies, rendering them ineffective when faced with even small environmental perturbations. In this work, we frame ACD as a two-player context-based partially observable Markov decision problem with observations represented as attributed graphs. This approach allows our agents to reason through the lens of relational inductive bias. Agents learn how to reason about hosts interacting with other system entities in a more general manner, and their actions are understood as edits to the graph representing the environment. By introducing this bias, we will show that our agents can better reason about the states of networks and zero-shot adapt to new ones. We show that this approach outperforms the state-of-the-art by a wide margin, and makes our agents capable of defending never-before-seen networks against a wide range of adversaries in a variety of complex, and multi-agent environments.

Maximally-Informative Retrieval for State Space Model Generation

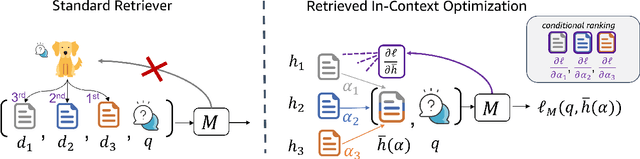
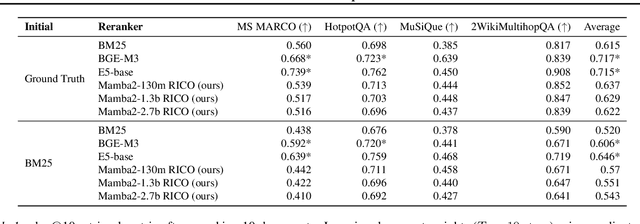
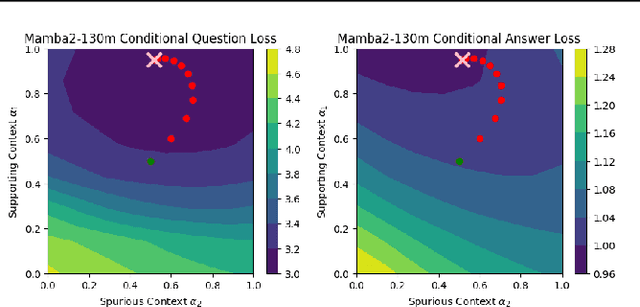
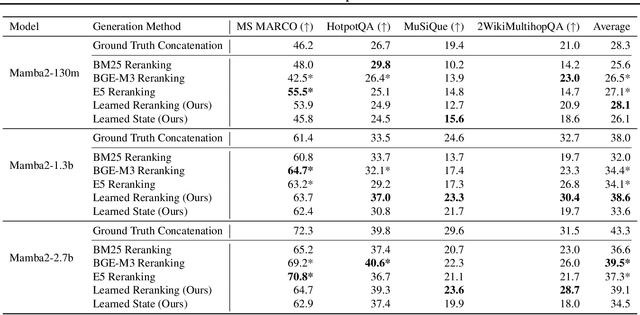
Given a query and dataset, the optimal way of answering the query is to make use all the information available. Modern LLMs exhibit impressive ability to memorize training data, but data not deemed important during training is forgotten, and information outside that training set cannot be made use of. Processing an entire dataset at inference time is infeasible due to the bounded nature of model resources (e.g. context size in transformers or states in state space models), meaning we must resort to external memory. This constraint naturally leads to the following problem: How can we decide based on the present query and model, what among a virtually unbounded set of known data matters for inference? To minimize model uncertainty for a particular query at test-time, we introduce Retrieval In-Context Optimization (RICO), a retrieval method that uses gradients from the LLM itself to learn the optimal mixture of documents for answer generation. Unlike traditional retrieval-augmented generation (RAG), which relies on external heuristics for document retrieval, our approach leverages direct feedback from the model. Theoretically, we show that standard top-$k$ retrieval with model gradients can approximate our optimization procedure, and provide connections to the leave-one-out loss. We demonstrate empirically that by minimizing an unsupervised loss objective in the form of question perplexity, we can achieve comparable retriever metric performance to BM25 with \emph{no finetuning}. Furthermore, when evaluated on quality of the final prediction, our method often outperforms fine-tuned dense retrievers such as E5.

Expansion Span: Combining Fading Memory and Retrieval in Hybrid State Space Models

The "state" of State Space Models (SSMs) represents their memory, which fades exponentially over an unbounded span. By contrast, Attention-based models have "eidetic" (i.e., verbatim, or photographic) memory over a finite span (context size). Hybrid architectures combine State Space layers with Attention, but still cannot recall the distant past and can access only the most recent tokens eidetically. Unlike current methods of combining SSM and Attention layers, we allow the state to be allocated based on relevancy rather than recency. In this way, for every new set of query tokens, our models can "eidetically" access tokens from beyond the Attention span of current Hybrid SSMs without requiring extra hardware resources. We describe a method to expand the memory span of the hybrid state by "reserving" a fraction of the Attention context for tokens retrieved from arbitrarily distant in the past, thus expanding the eidetic memory span of the overall state. We call this reserved fraction of tokens the "expansion span," and the mechanism to retrieve and aggregate it "Span-Expanded Attention" (SE-Attn). To adapt Hybrid models to using SE-Attn, we propose a novel fine-tuning method that extends LoRA to Hybrid models (HyLoRA) and allows efficient adaptation on long spans of tokens. We show that SE-Attn enables us to efficiently adapt pre-trained Hybrid models on sequences of tokens up to 8 times longer than the ones used for pre-training. We show that HyLoRA with SE-Attn is cheaper and more performant than alternatives like LongLoRA when applied to Hybrid models on natural language benchmarks with long-range dependencies, such as PG-19, RULER, and other common natural language downstream tasks.

B'MOJO: Hybrid State Space Realizations of Foundation Models with Eidetic and Fading Memory

We describe a family of architectures to support transductive inference by allowing memory to grow to a finite but a-priori unknown bound while making efficient use of finite resources for inference. Current architectures use such resources to represent data either eidetically over a finite span ("context" in Transformers), or fading over an infinite span (in State Space Models, or SSMs). Recent hybrid architectures have combined eidetic and fading memory, but with limitations that do not allow the designer or the learning process to seamlessly modulate the two, nor to extend the eidetic memory span. We leverage ideas from Stochastic Realization Theory to develop a class of models called B'MOJO to seamlessly combine eidetic and fading memory within an elementary composable module. The overall architecture can be used to implement models that can access short-term eidetic memory "in-context," permanent structural memory "in-weights," fading memory "in-state," and long-term eidetic memory "in-storage" by natively incorporating retrieval from an asynchronously updated memory. We show that Transformers, existing SSMs such as Mamba, and hybrid architectures such as Jamba are special cases of B'MOJO and describe a basic implementation, to be open sourced, that can be stacked and scaled efficiently in hardware. We test B'MOJO on transductive inference tasks, such as associative recall, where it outperforms existing SSMs and Hybrid models; as a baseline, we test ordinary language modeling where B'MOJO achieves perplexity comparable to similarly-sized Transformers and SSMs up to 1.4B parameters, while being up to 10% faster to train. Finally, we show that B'MOJO's ability to modulate eidetic and fading memory results in better inference on longer sequences tested up to 32K tokens, four-fold the length of the longest sequences seen during training.

SAFE: Machine Unlearning With Shard Graphs

We present Synergy Aware Forgetting Ensemble (SAFE), a method to adapt large models on a diverse collection of data while minimizing the expected cost to remove the influence of training samples from the trained model. This process, also known as selective forgetting or unlearning, is often conducted by partitioning a dataset into shards, training fully independent models on each, then ensembling the resulting models. Increasing the number of shards reduces the expected cost to forget but at the same time it increases inference cost and reduces the final accuracy of the model since synergistic information between samples is lost during the independent model training. Rather than treating each shard as independent, SAFE introduces the notion of a shard graph, which allows incorporating limited information from other shards during training, trading off a modest increase in expected forgetting cost with a significant increase in accuracy, all while still attaining complete removal of residual influence after forgetting. SAFE uses a lightweight system of adapters which can be trained while reusing most of the computations. This allows SAFE to be trained on shards an order-of-magnitude smaller than current state-of-the-art methods (thus reducing the forgetting costs) while also maintaining high accuracy, as we demonstrate empirically on fine-grained computer vision datasets.

À-la-carte Prompt Tuning : Combining Distinct Data Via Composable Prompting

We introduce \`A-la-carte Prompt Tuning (APT), a transformer-based scheme to tune prompts on distinct data so that they can be arbitrarily composed at inference time. The individual prompts can be trained in isolation, possibly on different devices, at different times, and on different distributions or domains. Furthermore each prompt only contains information about the subset of data it was exposed to during training. During inference, models can be assembled based on arbitrary selections of data sources, which we call "\`a-la-carte learning". \`A-la-carte learning enables constructing bespoke models specific to each user's individual access rights and preferences. We can add or remove information from the model by simply adding or removing the corresponding prompts without retraining from scratch. We demonstrate that \`a-la-carte built models achieve accuracy within $5\%$ of models trained on the union of the respective sources, with comparable cost in terms of training and inference time. For the continual learning benchmarks Split CIFAR-100 and CORe50, we achieve state-of-the-art performance.

Characterizing the Spectrum of the NTK via a Power Series Expansion

Under mild conditions on the network initialization we derive a power series expansion for the Neural Tangent Kernel (NTK) of arbitrarily deep feedforward networks in the infinite width limit. We provide expressions for the coefficients of this power series which depend on both the Hermite coefficients of the activation function as well as the depth of the network. We observe faster decay of the Hermite coefficients leads to faster decay in the NTK coefficients. Using this series, first we relate the effective rank of the NTK to the effective rank of the input-data Gram. Second, for data drawn uniformly on the sphere we derive an explicit formula for the eigenvalues of the NTK, which shows faster decay in the NTK coefficients implies a faster decay in its spectrum. From this we recover existing results on eigenvalue asymptotics for ReLU networks and comment on how the activation function influences the RKHS. Finally, for generic data and activation functions with sufficiently fast Hermite coefficient decay, we derive an asymptotic upper bound on the spectrum of the NTK.

Spectral Bias Outside the Training Set for Deep Networks in the Kernel Regime

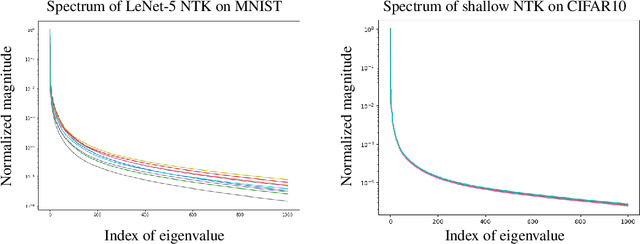
We provide quantitative bounds measuring the $L^2$ difference in function space between the trajectory of a finite-width network trained on finitely many samples from the idealized kernel dynamics of infinite width and infinite data. An implication of the bounds is that the network is biased to learn the top eigenfunctions of the Neural Tangent Kernel not just on the training set but over the entire input space. This bias depends on the model architecture and input distribution alone and thus does not depend on the target function which does not need to be in the RKHS of the kernel. The result is valid for deep architectures with fully connected, convolutional, and residual layers. Furthermore the width does not need to grow polynomially with the number of samples in order to obtain high probability bounds up to a stopping time. The proof exploits the low-effective-rank property of the Fisher Information Matrix at initialization, which implies a low effective dimension of the model (far smaller than the number of parameters). We conclude that local capacity control from the low effective rank of the Fisher Information Matrix is still underexplored theoretically.