Curvature Corrected Nonnegative Manifold Data Factorization

Data with underlying nonlinear structure are collected across numerous application domains, necessitating new data processing and analysis methods adapted to nonlinear domain structure. Riemannanian manifolds present a rich environment in which to develop such tools, as manifold-valued data arise in a variety of scientific settings, and Riemannian geometry provides a solid theoretical grounding for geometric data analysis. Low-rank approximations, such as nonnegative matrix factorization (NMF), are the foundation of many Euclidean data analysis methods, so adaptations of these factorizations for manifold-valued data are important building blocks for further development of manifold data analysis. In this work, we propose curvature corrected nonnegative manifold data factorization (CC-NMDF) as a geometry-aware method for extracting interpretable factors from manifold-valued data, analogous to nonnegative matrix factorization. We develop an efficient iterative algorithm for computing CC-NMDF and demonstrate our method on real-world diffusion tensor magnetic resonance imaging data.

Randomized Kaczmarz Methods with Beyond-Krylov Convergence

Randomized Kaczmarz methods form a family of linear system solvers which converge by repeatedly projecting their iterates onto randomly sampled equations. While effective in some contexts, such as highly over-determined least squares, Kaczmarz methods are traditionally deemed secondary to Krylov subspace methods, since this latter family of solvers can exploit outliers in the input's singular value distribution to attain fast convergence on ill-conditioned systems. In this paper, we introduce Kaczmarz++, an accelerated randomized block Kaczmarz algorithm that exploits outlying singular values in the input to attain a fast Krylov-style convergence. Moreover, we show that Kaczmarz++ captures large outlying singular values provably faster than popular Krylov methods, for both over- and under-determined systems. We also develop an optimized variant for positive semidefinite systems, called CD++, demonstrating empirically that it is competitive in arithmetic operations with both CG and GMRES on a collection of benchmark problems. To attain these results, we introduce several novel algorithmic improvements to the Kaczmarz framework, including adaptive momentum acceleration, Tikhonov-regularized projections, and a memoization scheme for reusing information from previously sampled equation~blocks.

Differentially Private Random Feature Model

Designing privacy-preserving machine learning algorithms has received great attention in recent years, especially in the setting when the data contains sensitive information. Differential privacy (DP) is a widely used mechanism for data analysis with privacy guarantees. In this paper, we produce a differentially private random feature model. Random features, which were proposed to approximate large-scale kernel machines, have been used to study privacy-preserving kernel machines as well. We consider the over-parametrized regime (more features than samples) where the non-private random feature model is learned via solving the min-norm interpolation problem, and then we apply output perturbation techniques to produce a private model. We show that our method preserves privacy and derive a generalization error bound for the method. To the best of our knowledge, we are the first to consider privacy-preserving random feature models in the over-parametrized regime and provide theoretical guarantees. We empirically compare our method with other privacy-preserving learning methods in the literature as well. Our results show that our approach is superior to the other methods in terms of generalization performance on synthetic data and benchmark data sets. Additionally, it was recently observed that DP mechanisms may exhibit and exacerbate disparate impact, which means that the outcomes of DP learning algorithms vary significantly among different groups. We show that both theoretically and empirically, random features have the potential to reduce disparate impact, and hence achieve better fairness.

Stratified Non-Negative Tensor Factorization

Non-negative matrix factorization (NMF) and non-negative tensor factorization (NTF) decompose non-negative high-dimensional data into non-negative low-rank components. NMF and NTF methods are popular for their intrinsic interpretability and effectiveness on large-scale data. Recent work developed Stratified-NMF, which applies NMF to regimes where data may come from different sources (strata) with different underlying distributions, and seeks to recover both strata-dependent information and global topics shared across strata. Applying Stratified-NMF to multi-modal data requires flattening across modes, and therefore loses geometric structure contained implicitly within the tensor. To address this problem, we extend Stratified-NMF to the tensor setting by developing a multiplicative update rule and demonstrating the method on text and image data. We find that Stratified-NTF can identify interpretable topics with lower memory requirements than Stratified-NMF. We also introduce a regularized version of the method and demonstrate its effects on image data.

Towards a Fairer Non-negative Matrix Factorization

Topic modeling, or more broadly, dimensionality reduction, techniques provide powerful tools for uncovering patterns in large datasets and are widely applied across various domains. We investigate how Non-negative Matrix Factorization (NMF) can introduce bias in the representation of data groups, such as those defined by demographics or protected attributes. We present an approach, called Fairer-NMF, that seeks to minimize the maximum reconstruction loss for different groups relative to their size and intrinsic complexity. Further, we present two algorithms for solving this problem. The first is an alternating minimization (AM) scheme and the second is a multiplicative updates (MU) scheme which demonstrates a reduced computational time compared to AM while still achieving similar performance. Lastly, we present numerical experiments on synthetic and real datasets to evaluate the overall performance and trade-offs of Fairer-NMF

Convergence of Manifold Filter-Combine Networks

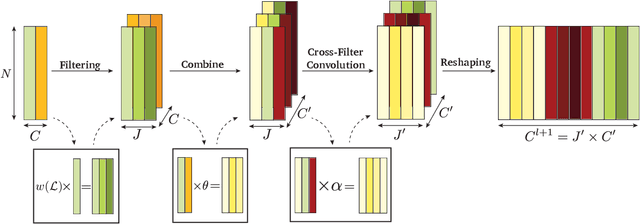
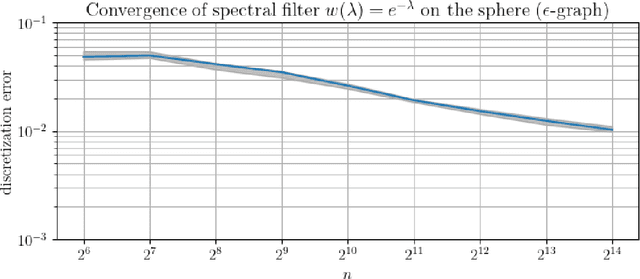
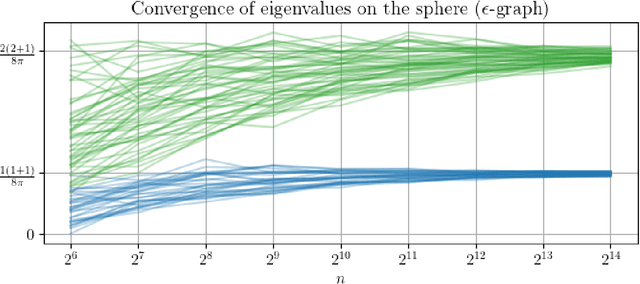
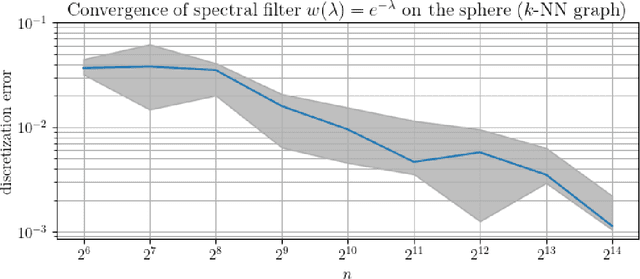
In order to better understand manifold neural networks (MNNs), we introduce Manifold Filter-Combine Networks (MFCNs). The filter-combine framework parallels the popular aggregate-combine paradigm for graph neural networks (GNNs) and naturally suggests many interesting families of MNNs which can be interpreted as the manifold analog of various popular GNNs. We then propose a method for implementing MFCNs on high-dimensional point clouds that relies on approximating the manifold by a sparse graph. We prove that our method is consistent in the sense that it converges to a continuum limit as the number of data points tends to infinity.

Fine-grained Analysis and Faster Algorithms for Iteratively Solving Linear Systems

While effective in practice, iterative methods for solving large systems of linear equations can be significantly affected by problem-dependent condition number quantities. This makes characterizing their time complexity challenging, particularly when we wish to make comparisons between deterministic and stochastic methods, that may or may not rely on preconditioning and/or fast matrix multiplication. In this work, we consider a fine-grained notion of complexity for iterative linear solvers which we call the spectral tail condition number, $\kappa_\ell$, defined as the ratio between the $\ell$th largest and the smallest singular value of the matrix representing the system. Concretely, we prove the following main algorithmic result: Given an $n\times n$ matrix $A$ and a vector $b$, we can find $\tilde{x}$ such that $\|A\tilde{x}-b\|\leq\epsilon\|b\|$ in time $\tilde{O}(\kappa_\ell\cdot n^2\log 1/\epsilon)$ for any $\ell = O(n^{\frac1{\omega-1}})=O(n^{0.729})$, where $\omega \approx 2.372$ is the current fast matrix multiplication exponent. This guarantee is achieved by Sketch-and-Project with Nesterov's acceleration. Some of the implications of our result, and of the use of $\kappa_\ell$, include direct improvement over a fine-grained analysis of the Conjugate Gradient method, suggesting a stronger separation between deterministic and stochastic iterative solvers; and relating the complexity of iterative solvers to the ongoing algorithmic advances in fast matrix multiplication, since the bound on $\ell$ improves with $\omega$. Our main technical contributions are new sharp characterizations for the first and second moments of the random projection matrix that commonly arises in sketching algorithms, building on a combination of techniques from combinatorial sampling via determinantal point processes and Gaussian universality results from random matrix theory.

Convergence and Complexity Guarantee for Inexact First-order Riemannian Optimization Algorithms

We analyze inexact Riemannian gradient descent (RGD) where Riemannian gradients and retractions are inexactly (and cheaply) computed. Our focus is on understanding when inexact RGD converges and what is the complexity in the general nonconvex and constrained setting. We answer these questions in a general framework of tangential Block Majorization-Minimization (tBMM). We establish that tBMM converges to an $\epsilon$-stationary point within $O(\epsilon^{-2})$ iterations. Under a mild assumption, the results still hold when the subproblem is solved inexactly in each iteration provided the total optimality gap is bounded. Our general analysis applies to a wide range of classical algorithms with Riemannian constraints including inexact RGD and proximal gradient method on Stiefel manifolds. We numerically validate that tBMM shows improved performance over existing methods when applied to various problems, including nonnegative tensor decomposition with Riemannian constraints, regularized nonnegative matrix factorization, and low-rank matrix recovery problems.

Kernel Alignment for Unsupervised Feature Selection via Matrix Factorization

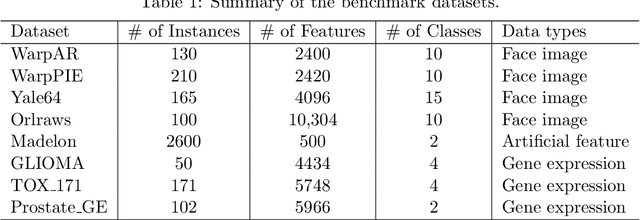
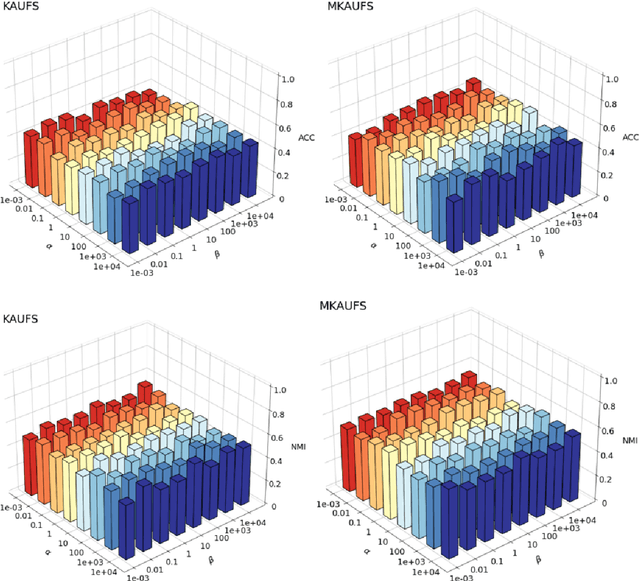
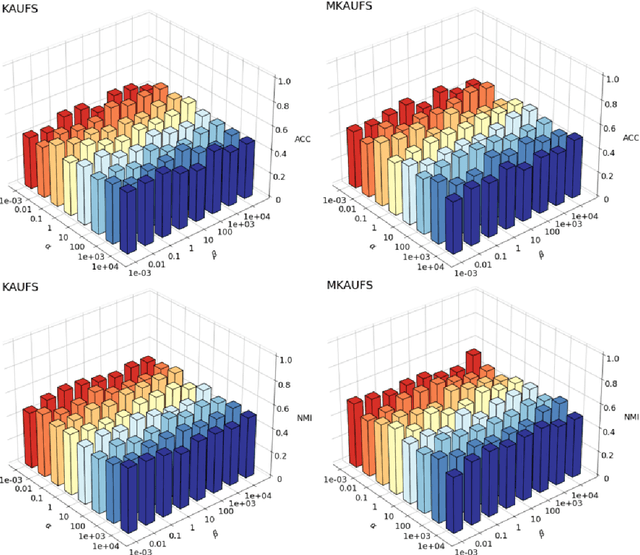
By removing irrelevant and redundant features, feature selection aims to find a good representation of the original features. With the prevalence of unlabeled data, unsupervised feature selection has been proven effective in alleviating the so-called curse of dimensionality. Most existing matrix factorization-based unsupervised feature selection methods are built upon subspace learning, but they have limitations in capturing nonlinear structural information among features. It is well-known that kernel techniques can capture nonlinear structural information. In this paper, we construct a model by integrating kernel functions and kernel alignment, which can be equivalently characterized as a matrix factorization problem. However, such an extension raises another issue: the algorithm performance heavily depends on the choice of kernel, which is often unknown a priori. Therefore, we further propose a multiple kernel-based learning method. By doing so, our model can learn both linear and nonlinear similarity information and automatically generate the most appropriate kernel. Experimental analysis on real-world data demonstrates that the two proposed methods outperform other classic and state-of-the-art unsupervised feature selection methods in terms of clustering results and redundancy reduction in almost all datasets tested.

Benign overfitting in leaky ReLU networks with moderate input dimension

The problem of benign overfitting asks whether it is possible for a model to perfectly fit noisy training data and still generalize well. We study benign overfitting in two-layer leaky ReLU networks trained with the hinge loss on a binary classification task. We consider input data which can be decomposed into the sum of a common signal and a random noise component, which lie on subspaces orthogonal to one another. We characterize conditions on the signal to noise ratio (SNR) of the model parameters giving rise to benign versus non-benign, or harmful, overfitting: in particular, if the SNR is high then benign overfitting occurs, conversely if the SNR is low then harmful overfitting occurs. We attribute both benign and non-benign overfitting to an approximate margin maximization property and show that leaky ReLU networks trained on hinge loss with Gradient Descent (GD) satisfy this property. In contrast to prior work we do not require near orthogonality conditions on the training data: notably, for input dimension $d$ and training sample size $n$, while prior work shows asymptotically optimal error when $d = \Omega(n^2 \log n)$, here we require only $d = \Omega\left(n \log \frac{1}{\epsilon}\right)$ to obtain error within $\epsilon$ of optimal.