Convergence of Manifold Filter-Combine Networks
Paper and Code
Oct 18, 2024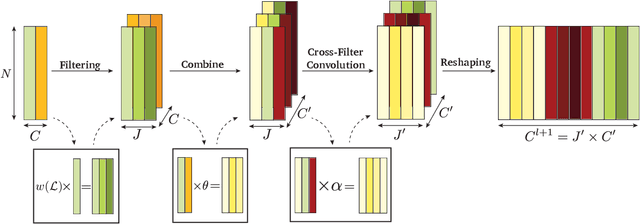
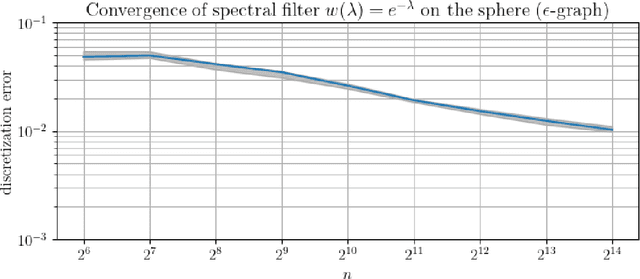
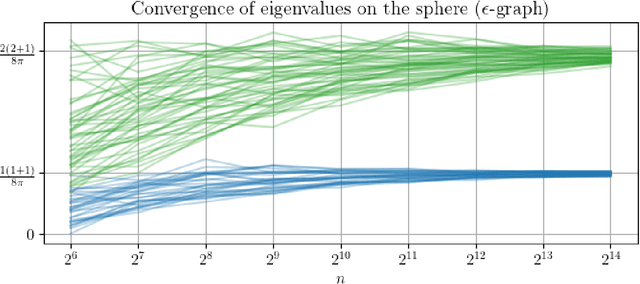
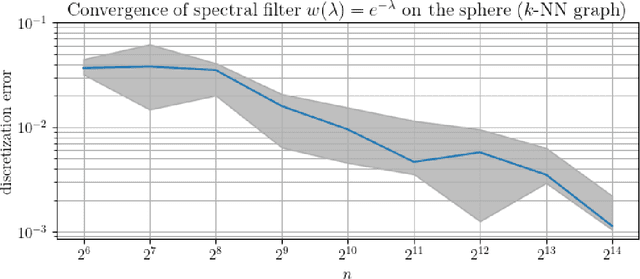
In order to better understand manifold neural networks (MNNs), we introduce Manifold Filter-Combine Networks (MFCNs). The filter-combine framework parallels the popular aggregate-combine paradigm for graph neural networks (GNNs) and naturally suggests many interesting families of MNNs which can be interpreted as the manifold analog of various popular GNNs. We then propose a method for implementing MFCNs on high-dimensional point clouds that relies on approximating the manifold by a sparse graph. We prove that our method is consistent in the sense that it converges to a continuum limit as the number of data points tends to infinity.
* Accepted to NeurIPS Workshop on Symmetry and Geometry in Neural
Representations (Extended Abstract Track)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge