Differentially Private Random Feature Model

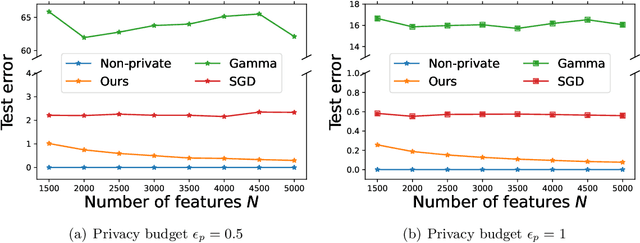
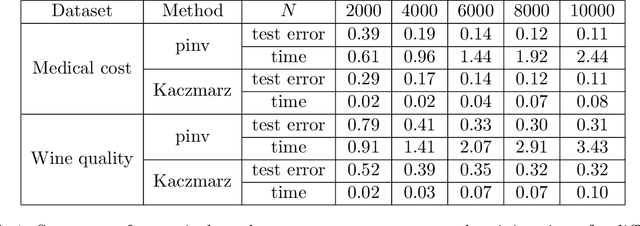
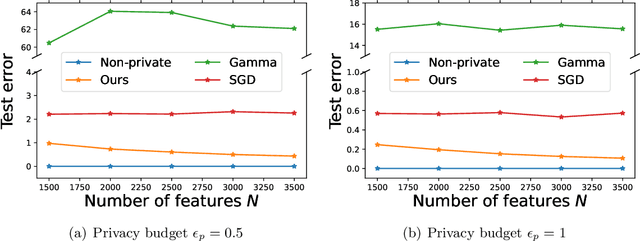
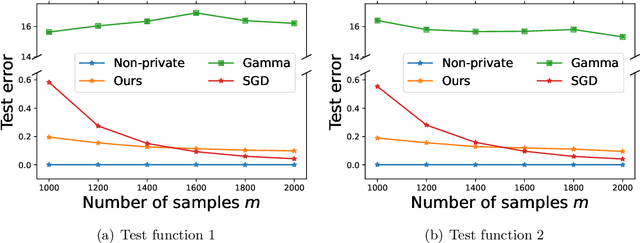
Designing privacy-preserving machine learning algorithms has received great attention in recent years, especially in the setting when the data contains sensitive information. Differential privacy (DP) is a widely used mechanism for data analysis with privacy guarantees. In this paper, we produce a differentially private random feature model. Random features, which were proposed to approximate large-scale kernel machines, have been used to study privacy-preserving kernel machines as well. We consider the over-parametrized regime (more features than samples) where the non-private random feature model is learned via solving the min-norm interpolation problem, and then we apply output perturbation techniques to produce a private model. We show that our method preserves privacy and derive a generalization error bound for the method. To the best of our knowledge, we are the first to consider privacy-preserving random feature models in the over-parametrized regime and provide theoretical guarantees. We empirically compare our method with other privacy-preserving learning methods in the literature as well. Our results show that our approach is superior to the other methods in terms of generalization performance on synthetic data and benchmark data sets. Additionally, it was recently observed that DP mechanisms may exhibit and exacerbate disparate impact, which means that the outcomes of DP learning algorithms vary significantly among different groups. We show that both theoretically and empirically, random features have the potential to reduce disparate impact, and hence achieve better fairness.

On the Optimal Recovery of Graph Signals

Learning a smooth graph signal from partially observed data is a well-studied task in graph-based machine learning. We consider this task from the perspective of optimal recovery, a mathematical framework for learning a function from observational data that adopts a worst-case perspective tied to model assumptions on the function to be learned. Earlier work in the optimal recovery literature has shown that minimizing a regularized objective produces optimal solutions for a general class of problems, but did not fully identify the regularization parameter. Our main contribution provides a way to compute regularization parameters that are optimal or near-optimal (depending on the setting), specifically for graph signal processing problems. Our results offer a new interpretation for classical optimization techniques in graph-based learning and also come with new insights for hyperparameter selection. We illustrate the potential of our methods in numerical experiments on several semi-synthetic graph signal processing datasets.

A Communication-Efficient Distributed Gradient Clipping Algorithm for Training Deep Neural Networks

In distributed training of deep neural networks or Federated Learning (FL), people usually run Stochastic Gradient Descent (SGD) or its variants on each machine and communicate with other machines periodically. However, SGD might converge slowly in training some deep neural networks (e.g., RNN, LSTM) because of the exploding gradient issue. Gradient clipping is usually employed to address this issue in the single machine setting, but exploring this technique in the FL setting is still in its infancy: it remains mysterious whether the gradient clipping scheme can take advantage of multiple machines to enjoy parallel speedup. The main technical difficulty lies in dealing with nonconvex loss function, non-Lipschitz continuous gradient, and skipping communication rounds simultaneously. In this paper, we explore a relaxed-smoothness assumption of the loss landscape which LSTM was shown to satisfy in previous works and design a communication-efficient gradient clipping algorithm. This algorithm can be run on multiple machines, where each machine employs a gradient clipping scheme and communicate with other machines after multiple steps of gradient-based updates. Our algorithm is proved to have $O\left(\frac{1}{N\epsilon^4}\right)$ iteration complexity for finding an $\epsilon$-stationary point, where $N$ is the number of machines. This indicates that our algorithm enjoys linear speedup. We prove this result by introducing novel analysis techniques of estimating truncated random variables, which we believe are of independent interest. Our experiments on several benchmark datasets and various scenarios demonstrate that our algorithm indeed exhibits fast convergence speed in practice and thus validates our theory.

Optimal Recovery from Inaccurate Data in Hilbert Spaces: Regularize, but what of the Parameter?

In Optimal Recovery, the task of learning a function from observational data is tackled deterministically by adopting a worst-case perspective tied to an explicit model assumption made on the functions to be learned. Working in the framework of Hilbert spaces, this article considers a model assumption based on approximability. It also incorporates observational inaccuracies modeled via additive errors bounded in $\ell_2$. Earlier works have demonstrated that regularization provide algorithms that are optimal in this situation, but did not fully identify the desired hyperparameter. This article fills the gap in both a local scenario and a global scenario. In the local scenario, which amounts to the determination of Chebyshev centers, the semidefinite recipe of Beck and Eldar (legitimately valid in the complex setting only) is complemented by a more direct approach, with the proviso that the observational functionals have orthonormal representers. In the said approach, the desired parameter is the solution to an equation that can be resolved via standard methods. In the global scenario, where linear algorithms rule, the parameter elusive in the works of Micchelli et al. is found as the byproduct of a semidefinite program. Additionally and quite surprisingly, in case of observational functionals with orthonormal representers, it is established that any regularization parameter is optimal.

Learning from Non-IID Data in Hilbert Spaces: An Optimal Recovery Perspective

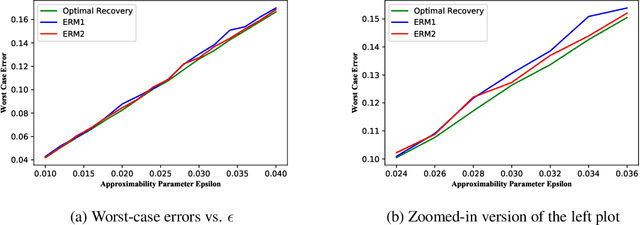
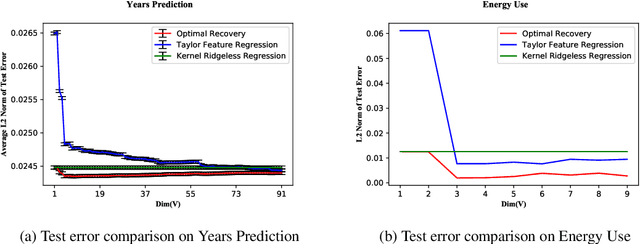
The notion of generalization in classical Statistical Learning is often attached to the postulate that data points are independent and identically distributed (IID) random variables. While relevant in many applications, this postulate may not hold in general, encouraging the development of learning frameworks that are robust to non-IID data. In this work, we consider the regression problem from an Optimal Recovery perspective. Relying on a model assumption comparable to choosing a hypothesis class, a learner aims at minimizing the worst-case (prediction) error, without recourse to IID assumption on data. We first develop a semidefinite program for calculating the worst-case error of any recovery map in finite-dimensional Hilbert spaces. Then, for any Hilbert space, we show that Optimal Recovery provides a formula which is user-friendly from an algorithmic point-of-view, as long as the hypothesis class is linear. Interestingly, this formula coincides with kernel ridgeless regression in some cases, proving that minimizing the average error and worst-case error can yield the same solution. We provide numerical experiments in support of our theoretical findings.