RedVisor: Reasoning-Aware Prompt Injection Defense via Zero-Copy KV Cache Reuse

Large Language Models (LLMs) are increasingly vulnerable to Prompt Injection (PI) attacks, where adversarial instructions hidden within retrieved contexts hijack the model's execution flow. Current defenses typically face a critical trade-off: prevention-based fine-tuning often degrades general utility via the "alignment tax", while detection-based filtering incurs prohibitive latency and memory costs. To bridge this gap, we propose RedVisor, a unified framework that synthesizes the explainability of detection systems with the seamless integration of prevention strategies. To the best of our knowledge, RedVisor is the first approach to leverage fine-grained reasoning paths to simultaneously detect attacks and guide the model's safe response. We implement this via a lightweight, removable adapter positioned atop the frozen backbone. This adapter serves a dual function: it first generates an explainable analysis that precisely localizes the injection and articulates the threat, which then explicitly conditions the model to reject the malicious command. Uniquely, the adapter is active only during this reasoning phase and is effectively muted during the subsequent response generation. This architecture yields two distinct advantages: (1) it mathematically preserves the backbone's original utility on benign inputs; and (2) it enables a novel KV Cache Reuse strategy, eliminating the redundant prefill computation inherent to decoupled pipelines. We further pioneer the integration of this defense into the vLLM serving engine with custom kernels. Experiments demonstrate that RedVisor outperforms state-of-the-art defenses in detection accuracy and throughput while incurring negligible utility loss.

Adaptive Algorithms with Sharp Convergence Rates for Stochastic Hierarchical Optimization

Hierarchical optimization refers to problems with interdependent decision variables and objectives, such as minimax and bilevel formulations. While various algorithms have been proposed, existing methods and analyses lack adaptivity in stochastic optimization settings: they cannot achieve optimal convergence rates across a wide spectrum of gradient noise levels without prior knowledge of the noise magnitude. In this paper, we propose novel adaptive algorithms for two important classes of stochastic hierarchical optimization problems: nonconvex-strongly-concave minimax optimization and nonconvex-strongly-convex bilevel optimization. Our algorithms achieve sharp convergence rates of $\widetilde{O}(1/\sqrt{T} + \sqrt{\bar{\sigma}}/T^{1/4})$ in $T$ iterations for the gradient norm, where $\bar{\sigma}$ is an upper bound on the stochastic gradient noise. Notably, these rates are obtained without prior knowledge of the noise level, thereby enabling automatic adaptivity in both low and high-noise regimes. To our knowledge, this work provides the first adaptive and sharp convergence guarantees for stochastic hierarchical optimization. Our algorithm design combines the momentum normalization technique with novel adaptive parameter choices. Extensive experiments on synthetic and deep learning tasks demonstrate the effectiveness of our proposed algorithms.

Wukong Framework for Not Safe For Work Detection in Text-to-Image systems

Text-to-Image (T2I) generation is a popular AI-generated content (AIGC) technology enabling diverse and creative image synthesis. However, some outputs may contain Not Safe For Work (NSFW) content (e.g., violence), violating community guidelines. Detecting NSFW content efficiently and accurately, known as external safeguarding, is essential. Existing external safeguards fall into two types: text filters, which analyze user prompts but overlook T2I model-specific variations and are prone to adversarial attacks; and image filters, which analyze final generated images but are computationally costly and introduce latency. Diffusion models, the foundation of modern T2I systems like Stable Diffusion, generate images through iterative denoising using a U-Net architecture with ResNet and Transformer blocks. We observe that: (1) early denoising steps define the semantic layout of the image, and (2) cross-attention layers in U-Net are crucial for aligning text and image regions. Based on these insights, we propose Wukong, a transformer-based NSFW detection framework that leverages intermediate outputs from early denoising steps and reuses U-Net's pre-trained cross-attention parameters. Wukong operates within the diffusion process, enabling early detection without waiting for full image generation. We also introduce a new dataset containing prompts, seeds, and image-specific NSFW labels, and evaluate Wukong on this and two public benchmarks. Results show that Wukong significantly outperforms text-based safeguards and achieves comparable accuracy of image filters, while offering much greater efficiency.

Complexity Lower Bounds of Adaptive Gradient Algorithms for Non-convex Stochastic Optimization under Relaxed Smoothness

Recent results in non-convex stochastic optimization demonstrate the convergence of popular adaptive algorithms (e.g., AdaGrad) under the $(L_0, L_1)$-smoothness condition, but the rate of convergence is a higher-order polynomial in terms of problem parameters like the smoothness constants. The complexity guaranteed by such algorithms to find an $\epsilon$-stationary point may be significantly larger than the optimal complexity of $\Theta \left( \Delta L \sigma^2 \epsilon^{-4} \right)$ achieved by SGD in the $L$-smooth setting, where $\Delta$ is the initial optimality gap, $\sigma^2$ is the variance of stochastic gradient. However, it is currently not known whether these higher-order dependencies can be tightened. To answer this question, we investigate complexity lower bounds for several adaptive optimization algorithms in the $(L_0, L_1)$-smooth setting, with a focus on the dependence in terms of problem parameters $\Delta, L_0, L_1$. We provide complexity bounds for three variations of AdaGrad, which show at least a quadratic dependence on problem parameters $\Delta, L_0, L_1$. Notably, we show that the decorrelated variant of AdaGrad-Norm requires at least $\Omega \left( \Delta^2 L_1^2 \sigma^2 \epsilon^{-4} \right)$ stochastic gradient queries to find an $\epsilon$-stationary point. We also provide a lower bound for SGD with a broad class of adaptive stepsizes. Our results show that, for certain adaptive algorithms, the $(L_0, L_1)$-smooth setting is fundamentally more difficult than the standard smooth setting, in terms of the initial optimality gap and the smoothness constants.

Personalized Federated Fine-tuning for Heterogeneous Data: An Automatic Rank Learning Approach via Two-Level LoRA

We study the task of personalized federated fine-tuning with heterogeneous data in the context of language models, where clients collaboratively fine-tune a language model (e.g., BERT, GPT) without sharing their local data, achieving personalization simultaneously. While recent efforts have applied parameter-efficient fine-tuning techniques like low-rank adaptation (LoRA) in federated settings, they typically use single or multiple independent low-rank adapters with predefined maximal and minimal ranks, which may not be optimal for diverse data sources over clients. To address this issue, we propose PF2LoRA, a new personalized federated fine-tuning algorithm built on a novel \emph{automatic rank learning approach via two-level LoRA}. Given the pretrained language model whose weight is frozen, our algorithm aims to learn two levels of adaptation simultaneously: the first level aims to learn a common adapter for all clients, while the second level fosters individual client personalization. A key advantage of PF2LoRA is its ability to adaptively determine a suitable rank based on an individual client's data, rather than relying on a predefined rank that is agnostic to data heterogeneity. We present a synthetic example that highlights how PF2LoRA automatically learns the ground-truth rank for each client, tailoring the adaptation to match the properties of their individual data. Notably, this approach introduces minimal additional memory overhead, as the second-level adaptation comprises a small number of parameters compared to the first level. Our experiments on natural language understanding and generation tasks demonstrate that PF2LoRA significantly outperforms existing federated fine-tuning methods.

On the Convergence of Adam-Type Algorithm for Bilevel Optimization under Unbounded Smoothness

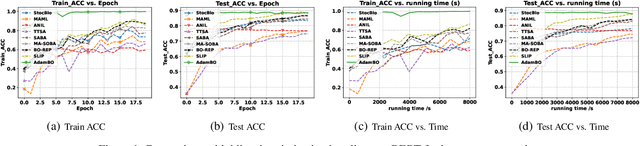
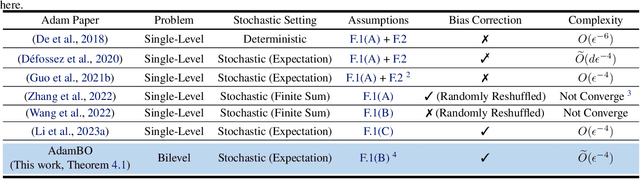
Adam has become one of the most popular optimizers for training modern deep neural networks, such as transformers. However, its applicability is largely restricted to single-level optimization problems. In this paper, we aim to extend vanilla Adam to tackle bilevel optimization problems, which have important applications in machine learning, such as meta-learning. In particular, we study stochastic bilevel optimization problems where the lower-level function is strongly convex and the upper-level objective is nonconvex with potentially unbounded smoothness. This unbounded smooth objective function covers a broad class of neural networks, including transformers, which may exhibit non-Lipschitz gradients. In this work, we introduce AdamBO, a single-loop Adam-type method that achieves $\widetilde{O}(\epsilon^{-4})$ oracle complexity to find $\epsilon$-stationary points, where the oracle calls involve stochastic gradient or Hessian/Jacobian-vector product evaluations. The key to our analysis is a novel randomness decoupling lemma that provides refined control over the lower-level variable. We conduct extensive experiments on various machine learning tasks involving bilevel formulations with recurrent neural networks (RNNs) and transformers, demonstrating the effectiveness of our proposed Adam-type algorithm.

Local Steps Speed Up Local GD for Heterogeneous Distributed Logistic Regression

We analyze two variants of Local Gradient Descent applied to distributed logistic regression with heterogeneous, separable data and show convergence at the rate $O(1/KR)$ for $K$ local steps and sufficiently large $R$ communication rounds. In contrast, all existing convergence guarantees for Local GD applied to any problem are at least $\Omega(1/R)$, meaning they fail to show the benefit of local updates. The key to our improved guarantee is showing progress on the logistic regression objective when using a large stepsize $\eta \gg 1/K$, whereas prior analysis depends on $\eta \leq 1/K$.

A Nearly Optimal Single Loop Algorithm for Stochastic Bilevel Optimization under Unbounded Smoothness

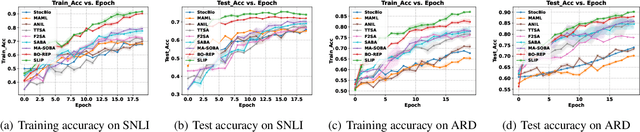
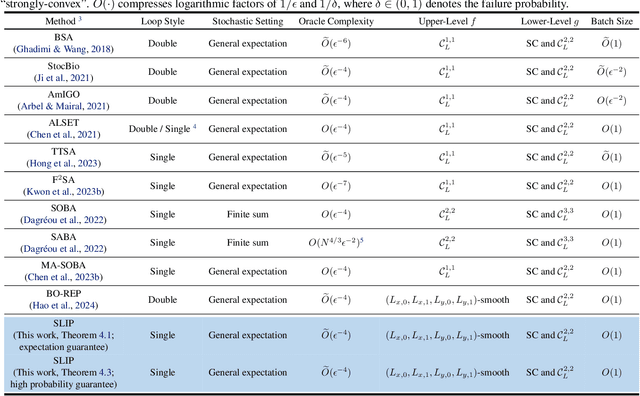
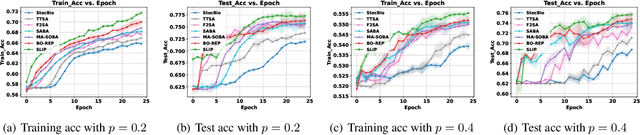
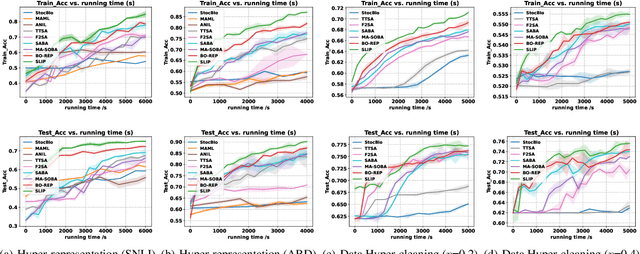
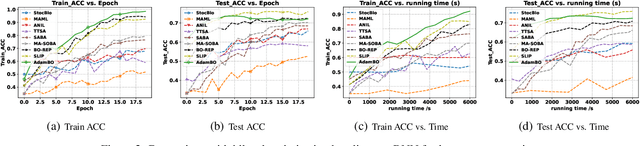
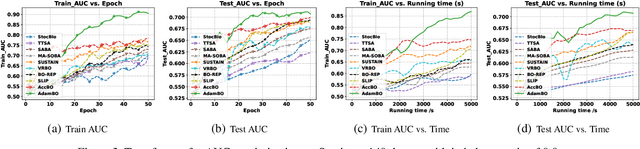
This paper studies the problem of stochastic bilevel optimization where the upper-level function is nonconvex with potentially unbounded smoothness and the lower-level function is strongly convex. This problem is motivated by meta-learning applied to sequential data, such as text classification using recurrent neural networks, where the smoothness constant of the upper-level loss function scales linearly with the gradient norm and can be potentially unbounded. Existing algorithm crucially relies on the nested loop design, which requires significant tuning efforts and is not practical. In this paper, we address this issue by proposing a Single Loop bIlevel oPtimizer (SLIP). The proposed algorithm first updates the lower-level variable by a few steps of stochastic gradient descent, and then simultaneously updates the upper-level variable by normalized stochastic gradient descent with momentum and the lower-level variable by stochastic gradient descent. Under standard assumptions, we show that our algorithm finds an $\epsilon$-stationary point within $\widetilde{O}(1/\epsilon^4)$\footnote{Here $\widetilde{O}(\cdot)$ compresses logarithmic factors of $1/\epsilon$ and $1/\delta$, where $\delta\in(0,1)$ denotes the failure probability.} oracle calls of stochastic gradient or Hessian-vector product, both in expectation and with high probability. This complexity result is nearly optimal up to logarithmic factors without mean-square smoothness of the stochastic gradient oracle. Our proof relies on (i) a refined characterization and control of the lower-level variable and (ii) establishing a novel connection between bilevel optimization and stochastic optimization under distributional drift. Our experiments on various tasks show that our algorithm significantly outperforms strong baselines in bilevel optimization.

Facet-Aware Multi-Head Mixture-of-Experts Model for Sequential Recommendation

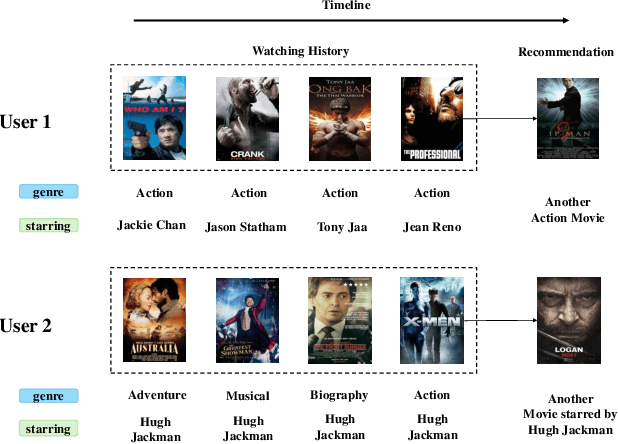
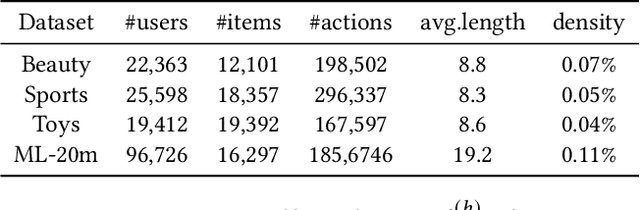
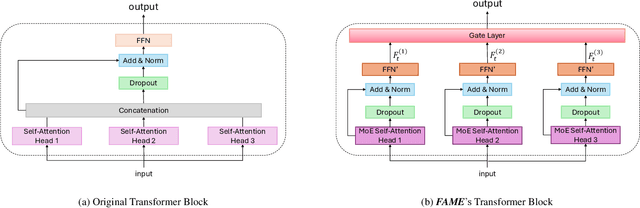
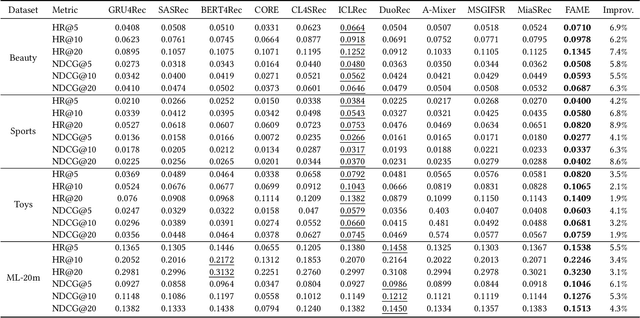
Sequential recommendation (SR) systems excel at capturing users' dynamic preferences by leveraging their interaction histories. Most existing SR systems assign a single embedding vector to each item to represent its features, and various types of models are adopted to combine these item embeddings into a sequence representation vector to capture the user intent. However, we argue that this representation alone is insufficient to capture an item's multi-faceted nature (e.g., movie genres, starring actors). Besides, users often exhibit complex and varied preferences within these facets (e.g., liking both action and musical films in the facet of genre), which are challenging to fully represent. To address the issues above, we propose a novel structure called Facet-Aware Multi-Head Mixture-of-Experts Model for Sequential Recommendation (FAME). We leverage sub-embeddings from each head in the last multi-head attention layer to predict the next item separately. This approach captures the potential multi-faceted nature of items without increasing model complexity. A gating mechanism integrates recommendations from each head and dynamically determines their importance. Furthermore, we introduce a Mixture-of-Experts (MoE) network in each attention head to disentangle various user preferences within each facet. Each expert within the MoE focuses on a specific preference. A learnable router network is adopted to compute the importance weight for each expert and aggregate them. We conduct extensive experiments on four public sequential recommendation datasets and the results demonstrate the effectiveness of our method over existing baseline models.

Federated Learning under Periodic Client Participation and Heterogeneous Data: A New Communication-Efficient Algorithm and Analysis

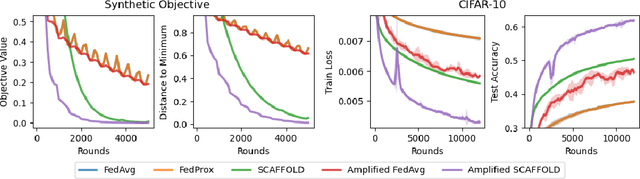
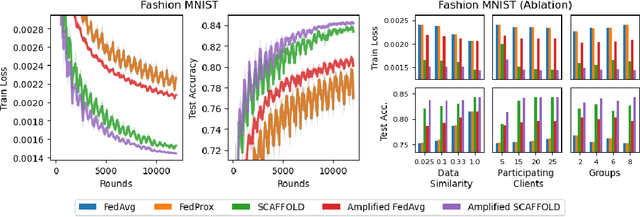
In federated learning, it is common to assume that clients are always available to participate in training, which may not be feasible with user devices in practice. Recent works analyze federated learning under more realistic participation patterns, such as cyclic client availability or arbitrary participation. However, all such works either require strong assumptions (e.g., all clients participate almost surely within a bounded window), do not achieve linear speedup and reduced communication rounds, or are not applicable in the general non-convex setting. In this work, we focus on nonconvex optimization and consider participation patterns in which the chance of participation over a fixed window of rounds is equal among all clients, which includes cyclic client availability as a special case. Under this setting, we propose a new algorithm, named Amplified SCAFFOLD, and prove that it achieves linear speedup, reduced communication, and resilience to data heterogeneity simultaneously. In particular, for cyclic participation, our algorithm is proved to enjoy $\mathcal{O}(\epsilon^{-2})$ communication rounds to find an $\epsilon$-stationary point in the non-convex stochastic setting. In contrast, the prior work under the same setting requires $\mathcal{O}(\kappa^2 \epsilon^{-4})$ communication rounds, where $\kappa$ denotes the data heterogeneity. Therefore, our algorithm significantly reduces communication rounds due to better dependency in terms of $\epsilon$ and $\kappa$. Our analysis relies on a fine-grained treatment of the nested dependence between client participation and errors in the control variates, which results in tighter guarantees than previous work. We also provide experimental results with (1) synthetic data and (2) real-world data with a large number of clients $(N = 250)$, demonstrating the effectiveness of our algorithm under periodic client participation.