Drop-Then-Recovery: How Redundant Are Vision-Language-Action Models?

Vision-Language-Action (VLA) models enable instruction-driven robotic manipulation, but they inherit oversized language backbones from pretrained VLMs whose capacity far exceeds what is needed for short robotic instructions. This raises a basic question: how much of a VLA model is actually necessary for closed-loop control? In this work, we study architectural redundancy in VLA models by using transformer block removal as a controlled intervention. We introduce \textbf{Drop-Then-Recovery (DTR)}, an analysis protocol that removes selected blocks from a pretrained VLA model and then fine-tunes the resulting model to measure whether the removed capacity was necessary for downstream control. To make this intervention reliable, we propose \textbf{GateProbe}, a one-shot virtual-gate sensitivity metric that ranks blocks by their contribution to the downstream action loss. Across multiple VLA architectures, manipulation benchmarks and even real-robot industrial scenarios, we find a strong asymmetry in post-removal recoverability: \ul{\textit{language backbones are highly redundant for standard robotic manipulation tasks, whereas vision and action pathways are substantially less tolerant to removal}}. On LIBERO, removing half of the LLM blocks even improves OpenVLA-OFT from 95.0% to 98.3% under the same downstream fine-tuning budget, and retaining only two language blocks still recovers baseline-level performance. These results suggest that current VLA benchmarks may exert limited pressure on deep language grounding and compositional instruction understanding, and that future VLA architectures should allocate capacity more deliberately across language, vision, and action components. The code is available at https://github.com/s1ghhh/VLADrop.

Adaptive Algorithms with Sharp Convergence Rates for Stochastic Hierarchical Optimization

Hierarchical optimization refers to problems with interdependent decision variables and objectives, such as minimax and bilevel formulations. While various algorithms have been proposed, existing methods and analyses lack adaptivity in stochastic optimization settings: they cannot achieve optimal convergence rates across a wide spectrum of gradient noise levels without prior knowledge of the noise magnitude. In this paper, we propose novel adaptive algorithms for two important classes of stochastic hierarchical optimization problems: nonconvex-strongly-concave minimax optimization and nonconvex-strongly-convex bilevel optimization. Our algorithms achieve sharp convergence rates of $\widetilde{O}(1/\sqrt{T} + \sqrt{\bar{\sigma}}/T^{1/4})$ in $T$ iterations for the gradient norm, where $\bar{\sigma}$ is an upper bound on the stochastic gradient noise. Notably, these rates are obtained without prior knowledge of the noise level, thereby enabling automatic adaptivity in both low and high-noise regimes. To our knowledge, this work provides the first adaptive and sharp convergence guarantees for stochastic hierarchical optimization. Our algorithm design combines the momentum normalization technique with novel adaptive parameter choices. Extensive experiments on synthetic and deep learning tasks demonstrate the effectiveness of our proposed algorithms.

On the Convergence of Adam-Type Algorithm for Bilevel Optimization under Unbounded Smoothness

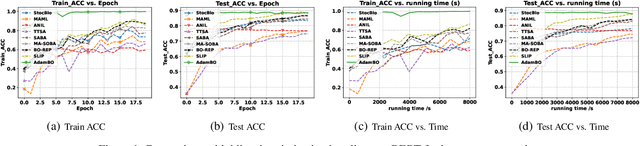
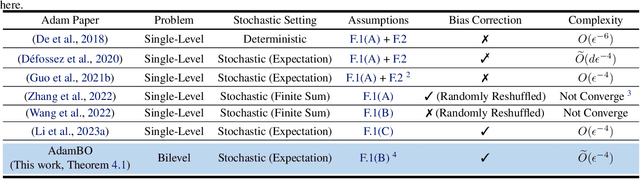
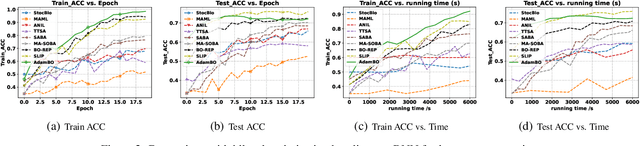
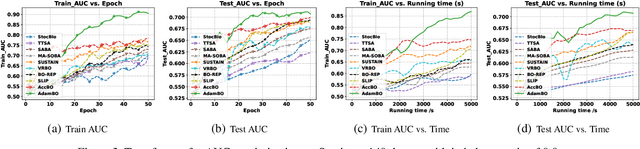
Adam has become one of the most popular optimizers for training modern deep neural networks, such as transformers. However, its applicability is largely restricted to single-level optimization problems. In this paper, we aim to extend vanilla Adam to tackle bilevel optimization problems, which have important applications in machine learning, such as meta-learning. In particular, we study stochastic bilevel optimization problems where the lower-level function is strongly convex and the upper-level objective is nonconvex with potentially unbounded smoothness. This unbounded smooth objective function covers a broad class of neural networks, including transformers, which may exhibit non-Lipschitz gradients. In this work, we introduce AdamBO, a single-loop Adam-type method that achieves $\widetilde{O}(\epsilon^{-4})$ oracle complexity to find $\epsilon$-stationary points, where the oracle calls involve stochastic gradient or Hessian/Jacobian-vector product evaluations. The key to our analysis is a novel randomness decoupling lemma that provides refined control over the lower-level variable. We conduct extensive experiments on various machine learning tasks involving bilevel formulations with recurrent neural networks (RNNs) and transformers, demonstrating the effectiveness of our proposed Adam-type algorithm.

A Nearly Optimal Single Loop Algorithm for Stochastic Bilevel Optimization under Unbounded Smoothness

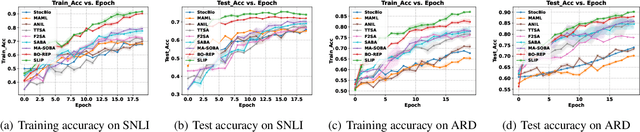
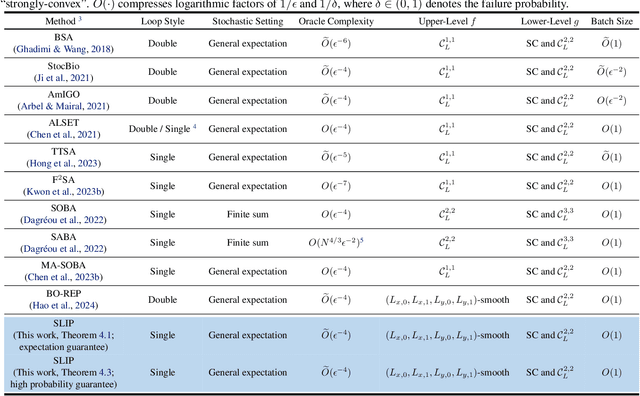
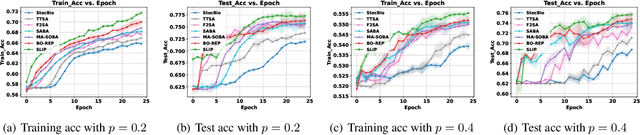
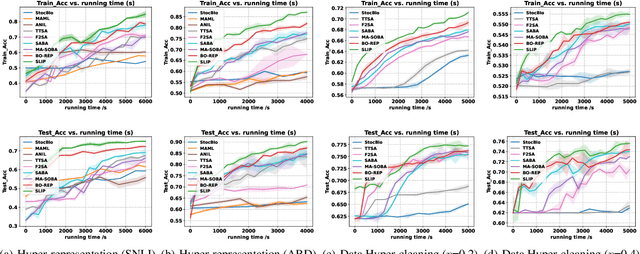
This paper studies the problem of stochastic bilevel optimization where the upper-level function is nonconvex with potentially unbounded smoothness and the lower-level function is strongly convex. This problem is motivated by meta-learning applied to sequential data, such as text classification using recurrent neural networks, where the smoothness constant of the upper-level loss function scales linearly with the gradient norm and can be potentially unbounded. Existing algorithm crucially relies on the nested loop design, which requires significant tuning efforts and is not practical. In this paper, we address this issue by proposing a Single Loop bIlevel oPtimizer (SLIP). The proposed algorithm first updates the lower-level variable by a few steps of stochastic gradient descent, and then simultaneously updates the upper-level variable by normalized stochastic gradient descent with momentum and the lower-level variable by stochastic gradient descent. Under standard assumptions, we show that our algorithm finds an $\epsilon$-stationary point within $\widetilde{O}(1/\epsilon^4)$\footnote{Here $\widetilde{O}(\cdot)$ compresses logarithmic factors of $1/\epsilon$ and $1/\delta$, where $\delta\in(0,1)$ denotes the failure probability.} oracle calls of stochastic gradient or Hessian-vector product, both in expectation and with high probability. This complexity result is nearly optimal up to logarithmic factors without mean-square smoothness of the stochastic gradient oracle. Our proof relies on (i) a refined characterization and control of the lower-level variable and (ii) establishing a novel connection between bilevel optimization and stochastic optimization under distributional drift. Our experiments on various tasks show that our algorithm significantly outperforms strong baselines in bilevel optimization.

An Accelerated Algorithm for Stochastic Bilevel Optimization under Unbounded Smoothness

This paper investigates a class of stochastic bilevel optimization problems where the upper-level function is nonconvex with potentially unbounded smoothness and the lower-level problem is strongly convex. These problems have significant applications in sequential data learning, such as text classification using recurrent neural networks. The unbounded smoothness is characterized by the smoothness constant of the upper-level function scaling linearly with the gradient norm, lacking a uniform upper bound. Existing state-of-the-art algorithms require $\widetilde{O}(1/\epsilon^4)$ oracle calls of stochastic gradient or Hessian/Jacobian-vector product to find an $\epsilon$-stationary point. However, it remains unclear if we can further improve the convergence rate when the assumptions for the function in the population level also hold for each random realization almost surely (e.g., Lipschitzness of each realization of the stochastic gradient). To address this issue, we propose a new Accelerated Bilevel Optimization algorithm named AccBO. The algorithm updates the upper-level variable by normalized stochastic gradient descent with recursive momentum and the lower-level variable by the stochastic Nesterov accelerated gradient descent algorithm with averaging. We prove that our algorithm achieves an oracle complexity of $\widetilde{O}(1/\epsilon^3)$ to find an $\epsilon$-stationary point. Our proof relies on a novel lemma characterizing the dynamics of stochastic Nesterov accelerated gradient descent algorithm under distribution drift with high probability for the lower-level variable, which is of independent interest and also plays a crucial role in analyzing the hypergradient estimation error over time. Experimental results on various tasks confirm that our proposed algorithm achieves the predicted theoretical acceleration and significantly outperforms baselines in bilevel optimization.

Bilevel Optimization under Unbounded Smoothness: A New Algorithm and Convergence Analysis

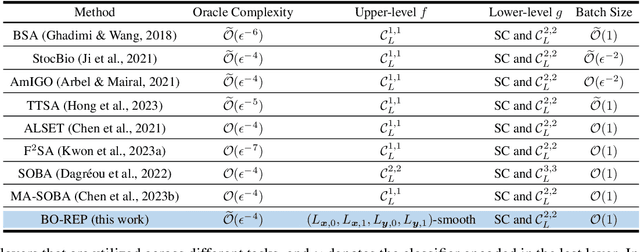
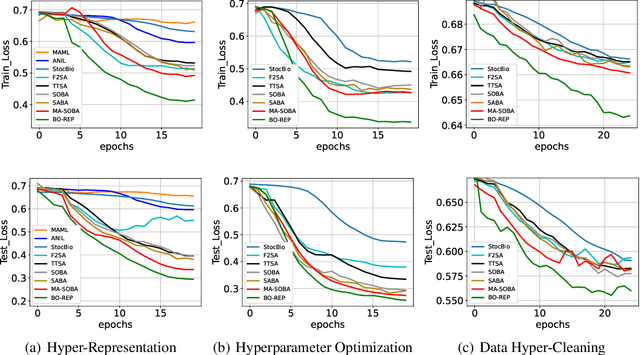
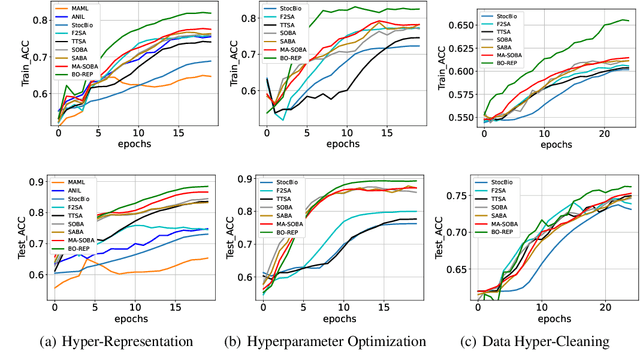
Bilevel optimization is an important formulation for many machine learning problems. Current bilevel optimization algorithms assume that the gradient of the upper-level function is Lipschitz. However, recent studies reveal that certain neural networks such as recurrent neural networks (RNNs) and long-short-term memory networks (LSTMs) exhibit potential unbounded smoothness, rendering conventional bilevel optimization algorithms unsuitable. In this paper, we design a new bilevel optimization algorithm, namely BO-REP, to address this challenge. This algorithm updates the upper-level variable using normalized momentum and incorporates two novel techniques for updating the lower-level variable: \textit{initialization refinement} and \textit{periodic updates}. Specifically, once the upper-level variable is initialized, a subroutine is invoked to obtain a refined estimate of the corresponding optimal lower-level variable, and the lower-level variable is updated only after every specific period instead of each iteration. When the upper-level problem is nonconvex and unbounded smooth, and the lower-level problem is strongly convex, we prove that our algorithm requires $\widetilde{\mathcal{O}}(1/\epsilon^4)$ iterations to find an $\epsilon$-stationary point in the stochastic setting, where each iteration involves calling a stochastic gradient or Hessian-vector product oracle. Notably, this result matches the state-of-the-art complexity results under the bounded smoothness setting and without mean-squared smoothness of the stochastic gradient, up to logarithmic factors. Our proof relies on novel technical lemmas for the periodically updated lower-level variable, which are of independent interest. Our experiments on hyper-representation learning, hyperparameter optimization, and data hyper-cleaning for text classification tasks demonstrate the effectiveness of our proposed algorithm.