On the Convergence of Adam-Type Algorithm for Bilevel Optimization under Unbounded Smoothness
Paper and Code
Mar 05, 2025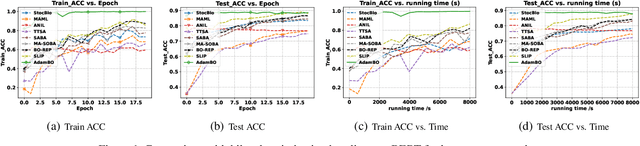
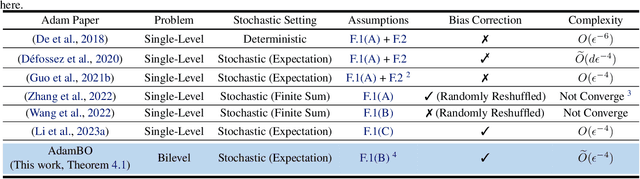
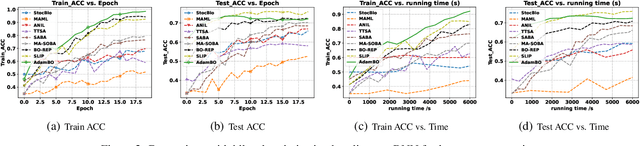
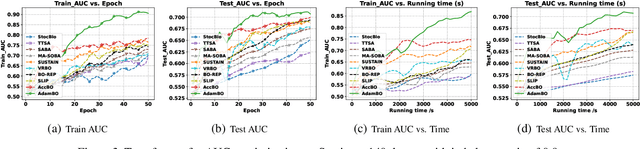
Adam has become one of the most popular optimizers for training modern deep neural networks, such as transformers. However, its applicability is largely restricted to single-level optimization problems. In this paper, we aim to extend vanilla Adam to tackle bilevel optimization problems, which have important applications in machine learning, such as meta-learning. In particular, we study stochastic bilevel optimization problems where the lower-level function is strongly convex and the upper-level objective is nonconvex with potentially unbounded smoothness. This unbounded smooth objective function covers a broad class of neural networks, including transformers, which may exhibit non-Lipschitz gradients. In this work, we introduce AdamBO, a single-loop Adam-type method that achieves $\widetilde{O}(\epsilon^{-4})$ oracle complexity to find $\epsilon$-stationary points, where the oracle calls involve stochastic gradient or Hessian/Jacobian-vector product evaluations. The key to our analysis is a novel randomness decoupling lemma that provides refined control over the lower-level variable. We conduct extensive experiments on various machine learning tasks involving bilevel formulations with recurrent neural networks (RNNs) and transformers, demonstrating the effectiveness of our proposed Adam-type algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge